ลำดับและอนุกรมและการประยุกต์
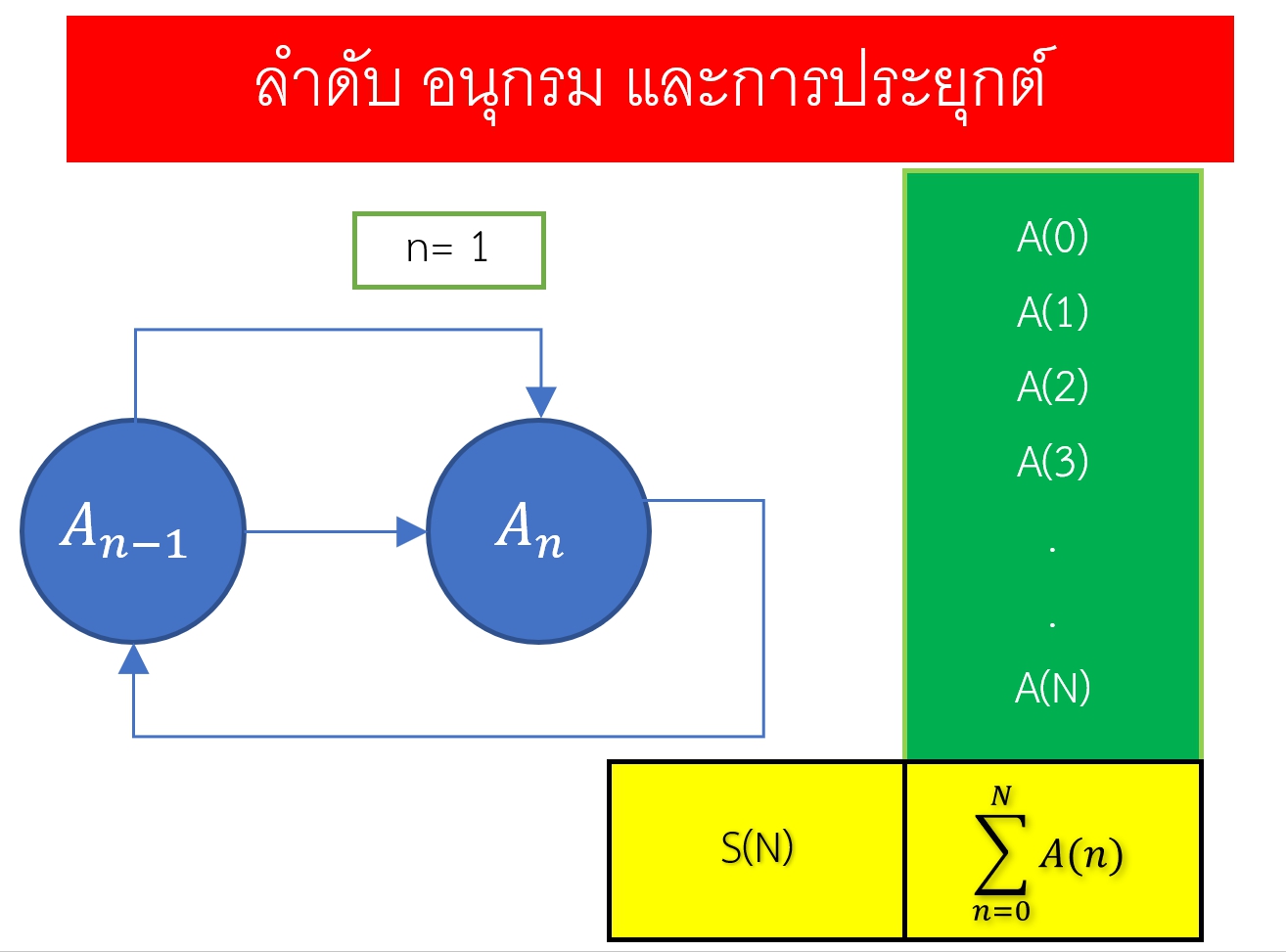
การนำตัวเลขมาจัดเรียงที่มีอันดับเรียงว่าลำดับ (sequence) เช่นการจัดเรียงจำนวนคู่ตั้งแต่ 0 ถึง 20 จะเขียนได้ในรูป 0, 2, 4, …, 20 กรณีที่เป็นจำนวนคี่จะสามารถเขียนได้ในรูป 1, 3, 5, …, 19 ลำดับในลักษณะข้างต้นนี้เราสามารถหาแบบรูปได้ โดยการสร้างฟังก์ชันในการหาค่าลำดับจากลำดับพจน์ของลำดับ ในที่นี้ถ้าเรากำหนดให้ลำดับของพจน์คือเซต { 1, 2, 3, …, N } โดยที่ N เป็นจำนวนนับ ซึ่งเป็นโดเมนของฟังก์ชันและเป็นเซตจำกัด โดยที่ฟังก์ชันค่าลำดับ A ส่งจากเซต { 1, 2, 3, …, N } ไปยังเรนจ์ในที่ให้เป็นจำนวนจริง
ค่าลำดับพจน์ที่ n เขียนแทนด้วย A(n)
เนื่องจากโดเมนลำดับเป็นเซตจำกัดเราจะเรียกว่าลำดับจำกัด (finite sequence) และลำดับที่มีโดเมนเป็นเซตอนันต์ {1, 2, 3, … } ว่าลำดับอนันต์ (infinite sequence) อย่างไรก็ตามเราอาจกำหนดโดเมนของลำดับเป็น whole number { 0, 1, 2, … } ก็ได้ ในที่นี้หากไม่ระบุโดเมนจะหมายถึงเซตของจำนวนนับ
พิจารณาลำดับ 0, 2, 4, …, 20
พจน์ที่ 1 คือ 0 = 2 x 0 = 2 x (1 - 1)
พจน์ที่ 2 คือ 2 = 2 x 1 =2 x (2 - 1)
พจน์ที่ 3 คือ 4 = 2 x 2 = 2 x (3 - 1)
…
พจน์ที่ 11 คือ 20 = 2 x 10 = 2 x (11 - 1)
พจน์ที่ n คือ A(n) =…………..= 2 x (n - 1)
สร้างฟังก์ชัน A(n) เป็นตัวแทนลำดับได้ดังนี้ ให้เซตโดเมนคือ { 1, 2, 3, …, 11 } แล้วลำดับ A(n) เป็นฟังก์ชันที่ส่งจาก { 1, 2, 3, …, 11 } ไปยังเซตของจำนวนจริงนิยามโดย A(n) = 2(n – 1) ในทำนองเดียวกันสำหรับ 1, 3, 5, …, 19 สำหรับลำดับนี้ A(n) ส่งจากเซต { 1, 2, 3, …, 10 } จะได้ A(n) = 2n - 1
อย่างไรก็ตามในธรรมชาติการเกิดขึ้นของลำดับจะขึ้นกับปริมาณที่มีอยู่ก่อนตัวอย่างเช่นลำดับฟิโบนักซี (Fibonacci sequence) อยู่ในรูป 1, 1, 2, 3, 5, 8, 13, … อธิบายแบบรูปได้ดังนี้
พจน์ที่ 1 คือพจน์เริ่มต้นค่าลำดับเท่ากับ 1
พจน์ที่ 2 คือพจน์เริ่มต้นค่าลำดับเท่ากับ 1
พจน์ที่ 3 เกิดจากผลรวม 2 พจน์ก่อนหน้าเท่ากับ 1 + 1 = 2
พจน์ที่ 4 เกิดจากผลรวม 2 พจน์ก่อนหน้าเท่ากับ 1 + 2 = 3
พจน์ที่ 5 เกิดจากผลรวม 2 พจน์ก่อนหน้าเท่ากับ 2 + 3 = 5
…
พจน์ที่ n เกิดจากผลรวม 2 พจน์ก่อนหน้าเท่ากับ A(n-1) + A(n-2)
การเขียนลำดับในลักษณะนี้เป็นการแสดงความสัมพันธ์ของพจน์ปัจจุบันที่พิจารณา กับ พจน์ก่อนหน้าเรียกว่าความสัมพันธ์ประเภทนี้ว่าความสัมพันธ์เวียนบังเกิด (Recurrence relation) ซึ่งประกอบด้วย 1) พจน์เริ่มต้น และ 2) ความสัมพันธ์ในรูปสมการ จากตัวอย่างข้างต้นนี้สามารถเขียนแทนได้ด้วยฟังก์ชัน
A(n) = A(n-1) + A(n-2) โดยที่ A(1) = 1 และ A(2) = 1
จากความสัมพันธ์ดังกล่าวสามารถคำนวณค่าพิจารณากรณีที่ n มากกว่าหรือเท่ากับ 3 ได้ดังนี้
A(3) = A(2) + A(1) = 1 + 1 = 2
A(4) = A(3) + A(2) = 2 + 1 = 3
A(5) = A(4) + A(3) = 3 + 2 = 5
A(6) = A(5) + A(4) = 5 + 3 = 8
A(7) = A(6) + A(5) = 8 + 5 = 13
การศึกษาคณิตศาสตร์ขั้นสูงจะมีการศึกษาวิธีการแก้สมการความสัมพันธ์เวียนเกิดเพื่อหาฟังก์ชันคำตอบ ผู้เขียนจะไม่กล่าวถึง ณ ที่นี้ ลักษณะและคุณสมบัติของลำดับที่ควรรู้ประกอบด้วย
- ลำดับเพิ่ม (increasing sequence): พจน์ถัดไปจะมีค่ามากกว่าพจน์ก่อนหน้าเสมอนั้นคือ
A(n) > A(n-1)
- ลำดับลด (decreasing sequence): พจน์ถัดไปจะมีค่าน้อยกว่าพจน์ก่อนหน้าเสมอนั้นคือ
A(n) < A(n-1)
-
ลำดับกวัดแกว่ง: ลำดับที่มีการเพิ่มลดสลับกันเช่น A(n) = (-1)n
-
ลำดับที่มีขอบเขต: ลำดับมีค่าอยู่ในช่วงจำนวนจริงเช่น A(n) = 1 – 1/n มีค่าอยู่ในช่วง [0,1)
อนุกรม (Series) คือผลรวมของลำดับ ผลรวมลำดับ n พจน์แรกเขียนแทนด้วย S(n)
พิจารณา sum ตั้งแต่ 1, 2, …, N
S(1) = A(1)
S(2) = A(1) + A(2)
…
S(n) = A(1) + A(2) + A(3) + … + A(N)
สรุปได้ว่า
S(n) = sum{ A(n) }
คุณสมบัติของ sum ตั้งแต่ 1, 2, …, N เบื้องต้น
-
sum{ k } = kN
-
sum{ n } = N(N + 1)/2
-
sum{ n2 } = N(N + 1)(2N + 1)/6
-
sum{ n3 } = [N(N + 1)/2 ]2
-
sum{ ka(n) + b(n) } = ksum{ a(n) } + sum{ b(n) }
ตัวอย่างที่ 1 จงหา S(n) เมื่อกำหนด A(n) = 2n – 3
วิธีทำ S(n) = sum{ A(n) }
= sum{ 2n – 3}
= sum{ 2n } – sum{ 3 }
= 2sum{ n } – sum {3}
= 2N(N+1)/2 – 3N
= N2 – 2N
ตัวอย่างที่ 2 จงหา S(n) เมื่อกำหนด A(n) = n2 – 2n3/3
วิธีทำ S(n) = sum{ A(n) }
= sum{ n2 – 2n3/3 }
= sum{ n2 } – (2/3)sum{ n3 }
= N(N+1)(2N+1)/6 – (2/3)N2(N+1)2/4
= (N4 + 4N3 + 4N2 + N)/6
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง (2559)
กลับไปที่เนื้อหา
ลำดับเลขคณิต และอนุกรมเลขคณิต
ลำดับเลขคณิต (Arithmetic sequence) คือลำดับที่มีการเพิ่มหรือลดคงที่ เขียนเป็นความสัมพันธ์เวียนเกิดได้ดังนี้
A(0) = a0 และ A(n) = A(n – 1) + d
เรียกค่าคงที่ d = A(n) – A(n – 1) ว่าผลต่างร่วม (common difference)
ตัวอย่างที่ 3 กำหนดให้ a0 = -5 และ d = 3 จงหา A(3)
A(0) = a0 = -5
A(1) = A(0) + d = -5 + 3 = -2
A(2) = A(1) + d = -2 + 3 = 1
A(3) = A(2) + d = 1 + 3 = 4
ในกรณีที่ N มีค่ามากๆ เช่นการหาค่า A(100) การทำซ้ำต้องใช้จำนวนครั้งในการคำนวณมากดังนั้นเราจึงหารูปแบบทั่วไปของลำดับได้ดังนี้
A(N) = A(N - 1) + d = A(N - 2) + 2d = A(N - 3) + 3d
สังเกตว่า A(N) = A(N – k) + kd
ถ้าให้ k = N – 1 จะได้ A(N) = A(N – (N – 1)) + (N – 1)d = A(1) + (N – 1)d
ถ้าให้ k = N จะได้ A(N) = A(N – N) + (N)d = A(0) + Nd
ตัวอย่างที่ 4 จากตัวอย่างที่ 3 จะได้ A(100) จะได้ A(100) = A(0) + 100(3) = -5 + 300 = 295
ในกรณีที่เรารู้ค่า A(k) และ d แต่ต้องการคำนวณค่า A(N)
ตัวอย่างที่ 5 กำหนดให้ A(5) = 12 และ d = 2 จงหาค่า A(30)
A(30) = A(30 – 25) + 25d = A(5) + 25d = 12 + 25 x 2 = 62
พิจารณาอนุกรมเลขคณิต (Arithmetic series) จากรูปแบบทั่วไปของลำดับเลขคณิต
A(n) = A(1) + (n – 1)d
พิจารณา sum ตั้งแต่ 1 ถึง N จะได้
S(N) = sum{ A(1) } + d sum{ (n – 1) }
จากคุณสมบัติของ sum จะได้
S(N) = A(1) x N + d(N – 1)(N)/2
= (N/2)[ 2a1 + (N – 1)d ]
กรณีที่เป็นการ sum ตั้งแต่ 0 ถึง N จะได้
S(N) = sum{ A(0) } + d sum{ n }
= N x A(0) + dN(N + 1)/2
= (N/2)[ 2a0 + (N + 1)d ]
สามารถเขียนในรูป
S(N) = (N/2)[ 2a0 + (N + 1)d ]
ตัวอย่างที่ 6 กำหนดให้ A = 250, 237, 224, 211, … จงหา S(25)
วิธีทำ เนื่องจากเรารู้ค่า a(0) = 250 และ สามารถหา d จาก 237 – 250 = -13 ดังนั้น
S(25) = (25/2)[ 2(250) + (25 + 1)(-13)] = (25/2)[ 500 – 338 ] = 2,025
จากสูตรทั้งสองข้อยังสามารถจัดรูปใหม่ได้เป็น
S(N) = (N/2)[ a1 + aN ]
ตัวอย่างที่ 7 กำหนดให้ a(1) = 10 และ a(10) = 145 จงหา S(10)
วิธีทำ จากสูตรข้างต้นจะพบว่า N = 10 ดังนั้น S(10) = (10/2)[ 10 + 145] = 775
ตัวอย่างที่ 8 กำหนดลำดับ log 2, log 4, log 8, … จงหาสูตรทั่วไปและพจน์รวม 10 พจน์แรก
วิธีทำ พิจารณาผลต่างรวมจะพบว่า log 4 – log 2 = log 2 = log 8 – log 4 จะเห็นได้ว่า d = log 2 เนื่องจาก a0 = log 2 ดังนั้นพจน์ทั่วไป a(n) = log 2 + n x log 2 = (n+1) log 2 พิจารณา
S(N) = sum { (n+1) log 2) } = (log 2) sum{ n+1 } = (log 2)[ (N+1)(N+2)/2]
ผลบวก 10 พจน์แรกคือ S(9) = (10)(11)/2 log 2 = 55 log 2
ตัวอย่างที่ 9 จงตรวจสอบว่า 218 อยู่ในลำดับเลขคณิต 5, 9, 13, 17, … หรือไม่
วิธีทำ จากลำดับที่กำหนดให้จะเห็นได้ว่า d = 4 และ a0 = 5 สมมติให้ 218 เป็นสมาชิกของลำดับจะได้ว่า
218 = a0 + nd = 5 + 4n
คำนวณค่า n = (218 – 5) / 4 = 53.25 ซึ่งไม่เป็นจำนวนนับ เกิดข้อขัดแย้งกับนิยามลำดับ ดังนั้น 218 ไม่เป็นสมาชิกของลำดับดังกล่าว
การวิเคราะห์ลำดับเลขคณิตและอนุกรมเลขคณิตเมื่อเราพิจารณาค่า d จะแบ่งได้เป็น 3 กรณีคือ
กรณีที่ 1 d = 0 ในกรณีนี้จะพบว่า a(n) – a(n-1) = 0 สำหรับทุกค่าจำนวนนับ n สรุปได้ว่า
a(n) = a(n-1) สำหรับทุกค่า n
นั้นคือลำดับ a(n) เป็นลำดับคงที่ เมื่อ n มีค่ามาก ๆ แล้ว a(n) จะยังคงมีค่าเท่าเดิม แต่ถ้าเราพิจารณาอนุกรมจะได้ S(n) = na0 เมื่อ n มีค่ามาก ๆแล้วจะทำให้ S(n) มีมากตามไปด้วยดังนั้นอนุกรมนี้เป็นอนุกรมลู่ออกเมื่อ a0 ไม่เท่ากับศูนย์ ถ้า a0 > 0 แล้วบวก S(n) จะลู่ออกไปยังบวกอนันต์ แต่ถ้า a0 < 0 แล้ว S(n) จะลู่ออกไปยังบวกอนันต์
กรณีที่ 2 d < 0 ในกรณีนี้จะพบว่า a(n) – a(n-1) = d < 0 สำหรับทุกค่าจำนวนนับ n สรุปได้ว่า
a(n) < a(n-1) สำหรับทุกค่า n
นั้นคือลำดับ a(n) เป็นลำดับลด แต่ถ้าเราพิจารณาอนุกรมจะได้ S(n) = (n/2)[ 2a1 + (n - 1)d ] เมื่อ n มีค่ามาก ๆแล้วจะทำให้ (n - 1)d มีค่าติดลบน้อยมากๆ ส่งผลให้พจน์ 2a1 + (n - 1)d มีค่าลบอนันต์เมื่อคูณกับ n/2 จะได้ผลคูณเป็นลบอนันต์ดังนั้น S(n) เป็นอนุกรมลู่ออกไปยังลบอนันต์
กรณีที่ 3 d > 0 ในกรณีนี้จะพบว่า a(n) – a(n-1) = d > 0 สำหรับทุกค่าจำนวนนับ n สรุปได้ว่า
a(n) > a(n-1) สำหรับทุกค่า n
นั้นคือลำดับ a(n) เป็นลำดับเพิ่ม แต่ถ้าเราพิจารณาอนุกรมจะได้ S(n) = (n/2)[ 2a1 + (n - 1)d ] เมื่อ n มีค่ามาก ๆแล้วจะทำให้ (n - 1)d มีค่ามากและเป็นบวก ส่งผลให้พจน์ 2a1 + (n - 1)d มีค่าบวกอนันต์เมื่อคูณกับ n/2 จะได้ผลคูณเป็นบวกอนันต์ดังนั้น S(n) เป็นอนุกรมลู่ออกไปยังบวกอนันต์
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง (2559)
กลับไปที่เนื้อหา
ลำดับเรขาคณิตและอนุกรมเรขาคณิต
ลำดับเรขาคณิต (Geometric sequence) คือลำดับที่มีพจน์ถัดไปเป็นสัดส่วนคงที่ของพจน์ก่อนหน้าเขียนเป็นความสัมพันธ์เวียนเกิดได้ดังนี้
A(0) = a0 และ A(n) = r x A(n – 1)
เรียกค่าคงที่ r = A(n) / A(n – 1) ว่าอัตราส่วนร่วม (common ratio) ในที่นี้เรากำหนดให้ r ไม่เท่ากับ 1 และ -1 เนื่องจาก ถ้า r = 1 จะได้ลำดับคงที่ ถ้า r = -1 จะได้ลำดับสลับ
ตัวอย่างที่ 10 กำหนดให้ a0 = 2/5 และ r = 3/2 จงหา A(3)
A(0) = a0 = 2/5
A(1) = r x A(0) = (3/2)(2/5) = 3/5
A(2) = r x A(1) = (3/2)(3/5) = 9/10
A(3) = r x A(2) = (3/2)(9/10) = 27/20
ในกรณีที่ N มีค่ามากๆ เช่นการหาค่า A(10) การทำซ้ำต้องใช้จำนวนครั้งในการคำนวณมากเช่นเดียวกันเราจึงหารูปแบบทั่วไปของลำดับได้ดังนี้
A(N) = r x A(N - 1) = r x (r x A(N – 2)) = r2 x A(N – 2) = r3 x A(N – 3)
สังเกตว่า A(N) = rk x A(N – k)
ถ้าให้ k = N – 1 จะได้ A(N) = rN-1 x A(N – (N – 1)) = rN-1 x A(1)
ถ้าให้ k = N จะได้ A(N) = rN x A(N – N) = rN x A(0)
ตัวอย่างที่ 11 จากตัวอย่างที่ 10 จะได้ A(10) จะได้ A(10) = rN x A(0) = (3/2)10 (2/5) = 310/(5 x 29)
ในกรณีที่เรารู้ค่า A(k) และ r แต่ต้องการคำนวณค่า A(N)
ตัวอย่างที่ 12 กำหนดให้ A(5) = 2048 และ r = 2-1 จงหาค่า A(15)
A(15) = r10 x A(15 – 10) = r10 x A(5) = 2-10 x 211 = 2
พิจารณาอนุกรมเรขาคณิตจากรูปแบบทั่วไปของลำดับเลขคณิต
A(n) = rna0 = rn-1a1
พิจารณา sum ตั้งแต่ 1 ถึง N จะได้
S(n) = sum{ A(n) } = sum{ rn-1a1 }
= a1 sum {rn-1}
จากสูตรการแยกตัวประกอบ
1 - rn = (1 – r)(1 + r + r2 + … + rn-1 }
จะเห็นได้ว่า
sum{ rn-1 } = (1 – rn)/(1 – r)
ดังนั้น
S(N) = [a1(1 – rN)]/(1 – r)
พิจารณา sum ตั้งแต่ 0 ถึง N จะได้
S(n) = sum{ A(n) } = sum{ rna0 }
= a0 sum {rn}
จากสูตรการแยกตัวประกอบ
1 - rn+1 = (1 – r)(1 + r + r2 + … + rn }
จะเห็นได้ว่า
sum{ rn } = (1 – rN+1)/(1 – r)
ดังนั้น
S(N) = [a0(1 – rN+1)]/(1 – r)
ในกรณีที่ N มีค่ามากๆ
ถ้า r > 1 แล้ว (1 – rN+1)]/(1 – r) มีค่าเป็นบวกอนันต์ทำให้ S(N) ขึ้นกับค่า a0 ถ้า a0 เป็นบวกแล้ว S(N) เมื่อ N มีค่ามาก ๆจะเป็นบวกอนันต์ แต่ถ้า a0 เป็นลบแล้ว S(N) เมื่อ N มีค่ามาก ๆจะเป็นลบอนันต์
ถ้า -1 < r < 1 แล้ว (1 – rN+1)]/(1 – r) มีค่าใกล้เคียงกับค่าคงที่ 1/(1 – r) เนื่องจาก rN+1 มีค่าเกือบเป็นศูนย์เมื่อ N มีค่ามาก ๆ จึงทำให้ S(N) มีค่าใกล้เคียงกับ a0 / (1 – r)
ถ้า r < -1 แล้ว (1 – rN+1)]/(1 – r) หาค่าไม่ได้
ตัวอย่างที่ 13 จงหารูปแบบคำตอบทั่วไปของ 1 + 2 + 22 + 23 + … + 2n และหาผลรวมของ 5 พจน์แรก
วิธีทำ จากอนุกรมที่กำหนดให้จะเห็นว่า a(n)/a(n-1) = 2 สำหรับทุกค่า n ที่เป็นจำนวนนับ ดังนั้นอนุกรมนี้เป็นอนุกรมเรขาคณิตที่มีพจน์เริ่มต้นคือ a1 = 1 และ พจน์สิ้นสุดคือ 2n จากสูตรจะได้ว่า
S(n) = [a1(1 – rN)]/(1 – r) = (1-2n)/(-1) = 2n – 1
อนุกรมเป็นผลรวมลำดับเลขคณิตที่อยู่ในรูป a(n) = a1rn-1 5 สำหรับ n ที่เป็นจำนวนนับดังนั้น 5 พจน์แรกสอดคล้องกับ n = 1,2,..,5 จะได้ S(n) = 1 + 2 + 4 + 8 +16 จากสูตรคำนวณ
S(n) = 1(1 – 25)/(1 – 2) = 31
ตัวอย่างที่ 14 จงหาค่าของ 1 + 3/2 + (3/2)2 + …
วิธีทำ อนุกรมที่กำหนดให้เป็นอนุกรมเรขาคณิตจากลำดับเรขาคณิต a(n) = a1rn-1 โดยที่ a1 = 1 และ r = 3/2 เนื่องจากค่า r > 1 และ a1 > 0 ทำให้อนุกรมลู่ออกไปสู่บวกอนันต์ดังนั้นอนุกรมนี้หาค่าไม่ได้
ตัวอย่างที่ 15 จงหาสูตรทั่วไปของ 5 + 5 x 3-1 + 5 x 3-2 + … + 5 x 3-m+5 และพิจารณาว่าถ้า m มีค่ามาก ๆเป็นอนันต์แล้วอนุกรมนี้หาค่าได้หรือไม่ ถ้าหาได้มีค่าเท่าใด
วิธีทำ อนุกรม 5 + 5 x 3-1 + 5 x 3-2 + … + 5 x 3-m+5 มีพจน์ a1 = 5 และมีอัตราส่วนร่วม r = 3-1 = 1/3 เป็นอนุกรมเรขาคณิตรูปแบบทั่วไปของอนุกรมคือ
S(m) = 5(1 – 3-m+6) / (1 – 3-1)
ให้ m มีค่ามากๆเป็นอนันต์อนุกรมข้างต้นคือ 5 + 5 x 3-1 + 5 x 3-2 + … เนื่องจากค่า r < 1 ดังนั้นอนุกรมนี้ลู่เข้าสู่
S = 5/(1 – 3-1) = 15/2 = 7.5
ตัวอย่างที่ 17 กำหนดลำดับ xn , xn-1y, xn-2y2 , …, xyn-1, yn จงหาพจน์ตัวไปและผลบวกของลำดับที่กำหนดให้
วิธีทำ ลำดับนี้เป็นลำดับเรขาคณิต n + 1 พจน์ที่มี a0 = xny0 โดยที่อัตราส่วนรวม r = y/x จะได้รูปแบบทั่วไปของลำดับคือ
a(N) = xn(y/x)N สำหรับ N = 0, 1, 2, …, n
สอดคล้องกับพจน์สุดท้าย an = xn(y/x)n = yn พิจารณาค่าอนุกรม เนื่องจากเป็นลำดับจำกัดทำให้ค่าอนุกรมหาค่าได้และสมมติให้เท่ากับ S จากสูตร
S = S(n) = [a0(1 – rn+1)]/(1 – r)
= xn(1 – (y/x)n+1)/(1 – y/x)
= (xn+1 – yn+1)/(x – y)
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง (2559)
กลับไปที่เนื้อหา
-
คำที่เกี่ยวข้อง



