ฟังก์ชันตรีโกณมิติมีความสำคัญมากในการศึกษาศาสตร์สาขาต่าง ( ทั้งทางด้านคณิตศาสตร์และวิทยาศาสตร์เนื่องจากการเปลี่ยนแปลงของปริมาณต่าง " ในธรรมซาติในหลายกรณีมีลักษณะคล้ายฟังก์ชันตรีโกณมิติ ซึ่งเป็นฟังก์ชันที่เป็นคาบ เมื่อสังกตกราฟของฟังก์ชันตรีโกณมิติ จะพบว่า กราฟมีลักษณะซ้ำกันเป็นช่วง ตัวอย่างเช่น กราฟของฟังก์ชันไซน์และฟังก์ชันโคไซน์

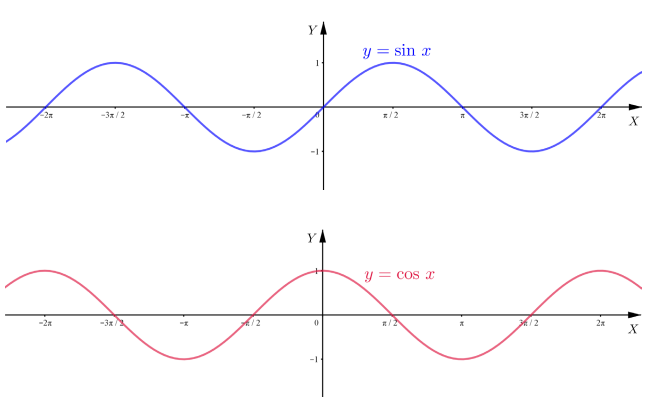
ภาพ 1 กราฟของฟังก์ชันไซน์และฟังก์ชันโคไซน์

          บทความนี้จะเสนอการนำฟังก์ชันตรีโกณมิติไปใช้ในการอธิบายปรากฏการณ์ข้างขึ้นข้างแรม ก่อนอื่นเราต้องรู้ที่มาของปรากฏการณ์นี้ก่อน

ดิถีของดวงจันทร์ (Phases of the moon)

          ดิถีของดวงจันทร์หรือปรากฏการณ์ข้างขึ้นข้างแรม เกิดจากการที่ดวงจันทร์ได้รับแสงจากดวงอาทิตย์และใคจรรอบโลก ทำให้คนบนโลกเห็นแสงสะท้อนจากดวงจันทร์แตกต่างกันไปในแต่ละคืน โดยดวงจันทร์ใช้เวลาในการโคจรรอบโลกประมาณ 29.5 วัน การที่เราสังเกตเห็นดวงจันทร์สว่างเต็มดวง แล้วส่วนสว่างค่อย ๆ ลดลงจนกระทั่งมืดทั้งดวง เรียกช่วงตังกล่าวว่า ข้างแรม (Waning) วันที่ดวงจันทร์มืดทั้งดวง เรียกวันแรม 15 ค่ำหรือ จันทร์ดับ (New moon) ซึ่งเป็นวันที่ดวงจันทร์อยู่ระหว่างโลกกับดวงอาทิตย์ หลังจากนั้นดวงจันทร์จะค่อย ๆ สว่างจนเต็มดวงอีกครั้ง เรียกช่วงนี้ว่า ข้างขึ้น (Waxing) โดยให้วันที่ดวงจันทร์สว่างเต็มดวงเป็นวันขึ้น 15 ค่ำหรือเรียกว่า จันทร์เพ็ญ (Full moon) ซึ่งเป็นวันที่ดวงจันทโคจรมาอยู่ด้านตรงข้ามกับดวงอาทิตย์ ส่วนวันที่ดวงจันทร์เคลื่อนที่ทำมุมฉากกับโลกและดวงอาทิตย์ จะทำให้เราเห็นดวงจันทร์สว่างครึ่งดวง เรียกวันแรม 8 ค่ำ หรือวันขึ้น 8 ค่ำ

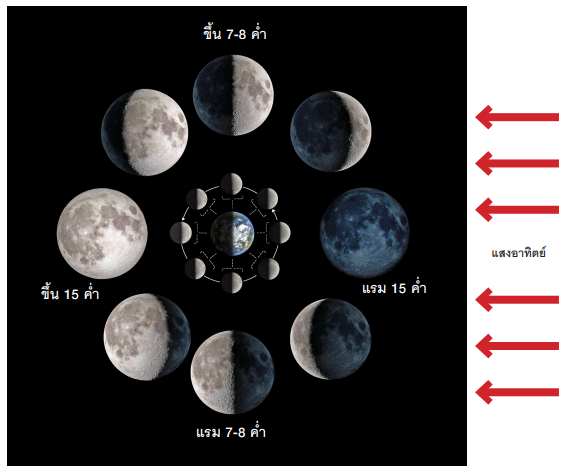
ภาพ 2  ส่วนสว่างของดวงจันทร์ ณ ตำแหน่งต่าง ๆ ขณะโคจรรอบโลกภาพดวงจันทร์ที่อยู่วงนอก เป็นภาพที่ผู้สังเกตบนโลกเห็น

          สังเกตได้ว่า ปรากฏการณ์ข้างขึ้นข้างแรมเป็นปรากฏกรณ์ที่เกิดขึ้นในรูปแบบที่ซ้ำกันเป็นช่วง ๆ โดยแต่ละช่วงใช้เวลาประมาณ 29.5 วัน ตามระยะเวลาการโคจรรอบลกของตวงจันทร์ หากเริ่มสังเกตจากวันแรม 15 ค่ำ ซึ่งเป็นวันที่เราไม่สามารถเห็นส่วนสว่างของดวงจันทร์ วันต่อมาจะเป็นวันขึ้น 1 ค่ำ และต่อมาจะเป็นวันขึ้น 2 ค่ำ ไปเรื่อย ๆ โดยส่วนสว่างของดวงจันทร์ที่มองเห็นได้ก็จะเพิ่มขึ้นไปเรื่อย ๆ ในแต่ละวัน จนถึงวันขึ้น 15 ค่ำ ซึ่งเป็นวันที่เราเห็นดวงจันทร์สว่างเต็มดวงต่อจากนั้นวันต่อมาจะเป็นวันแรม 1 ค่ำ และวันแรม 2 ค่ำ ไปเรื่อย ๆ โดยส่วนสว่างของดวงจันทร์ที่มองเห็นได้จะลดลงไปเรื่อย ๆ ในแต่ละวัน จนถึงวันแรม 15 ค่ำ

          ดังนั้นจะเห็นได้ว่าปรากฏการณ์ข้างขึ้นข้างแรมมีลักษณะเทียบเคียงได้กับพฤติกรรมของฟังก็ชันตรีโกณมิติ ซึ่งเป็นฟังก์ชันที่เป็นคาบดังที่กล่าวในตอนต้น ถ้าสมมติให้วงโคจรของดวงจันทร์รอบโลกเป็นวงกลม และกำหนดให้โลกอยู่ที่จุดกำเนิด 0 ดวงจันทร์อยู่ที่จุด M ดวงอาทิตย์อยู่ที่จุด S และ X แทนมุม M0S จะสามารถจำลองการเกิดปรากฏการณ์ข้างขึ้นข้างแรมได้ดังรูป

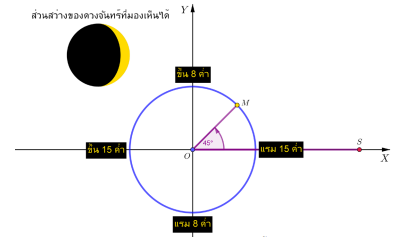
ภาพ 3 กราฟจำลองการเกิดปรากฏการณ์ข้างขึ้นข้างแรม

หมายเหตุ สามารถเข้าไปที่เว็บไซต์ https://www.geogebra.org/m/TbT5zz75 
เพื่อดูภาพเคลื่อนไหวของกราฟจำลองปรากฏการณ์ข้างขึ้นข้างแรม

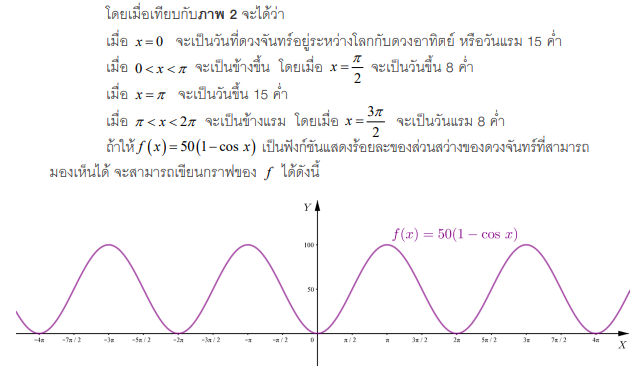
ภาพ 4 กราฟของฟังก็ชัน f

          จะเห็นว่า โดเมนของฟังก์ชัน  คือ เซตของจำนวนจริง เรนจ์ของฟังก์ชัน f คือ [0,100] คาบของฟังก์ชันคือ 27 และแอมพลิจูดของฟังก็ชัน f คือ 50

          การนำฟังก์ขันตรีโกณมิติมาอธิบายปรากฏการณ์ข้างขึ้นข้างแรมดังที่ได้แสดงข้างตันนอกจากจะช่วยให้ผู้เรียนสามารถข้าใจปรากการณ์ดังกล่าวได้ดีขึ้นแล้ว ยังจะทำให้ผู้เรียนเห็นประโยซน์ของฟังก์ชันตโกณมิติ และเห็นความเชื่อมโยงของคณิตศาสตร์กับชีวิตจริง ซึ่งจะช่วยให้การเรียนในชั้นเรียนน่าสนใจและไม่น่าเบื่อด้วย

          นอกจากนี้ ฟังก์ชันตรีโกณมิติยังสามารถนำไปใช้ในการศึกษาเรื่องอื่น ๆ ได้อีกมาก เช่น ใช้ในการศึกษาเรื่องคลื่นเสียงและคลื่นแสง่ในวิชาฟิสิกส์ใช้คาดการณ์อุณหภูมิในฤดูกาลต่าง ๆในวิชาอุนิยมวิทยา เป็นต้น หากผู้สอนสามารถแสดงให้เห็นความเชื่อมโยงของคณิตศาสตร์กับศาสตร์อื่น ๆ และชีวิตจริงได้ ดังตัวอย่างในบทความนี้ จะช่วยให้ผู้เรียนเห็นประโยชน์ของคณิตศาสตร์ ซึ่งเป็นพื้นฐานสำคัญในการศึกษาศาสตร์อื่น ๆ ตลอดจนการพัฒนาด้านวิทยาศาสตร์และเทคโนโลยี สิ่งเหล่านี้จะช่วยจุดประกายความคิดของผู้เรียน และเป็นแรงบันดาลใจในการเรียนคณิตศาสตร์ให้แก่ผู้เรียนที่จะเติบโตเป็นกำลังสำคัญในการพัฒนาประเทศต่อไปในอนาคต

          บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Frosty Drew Observatory & Sky Theatre. (October 1999). Phases of the Moon. Retrieved November 12. 2017,from https://frostydrew.org/observatory/columns/1999/oct.htm.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคนโลยี. (2554). คู่มือครูรายวิชาพื้นฐานวิทยาศาสตร์ วิทยาศาสตร์ 6 ขั้นมัธยมศึกษาปีที่ 3 เล่ม 2 กลุ่มสาระการเรียนรู้วิทยาศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551. กรุงเทพมหานคร: โรงพิมพ์ สกสค. ลาดพร้าว.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2554). หนังสือเรียนรายวิชาพื้นฐานวิทยาศาสตร์ วิทยาศาสตร์ 6 ขั้นมัธยมศึกษาปีที่ 3 เล่ม 2 กลุ่มสาระการเรียนรู้วิทยาศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551. กรุงเทพมหานคร: โรงพิมพ์ สกสค.ลาดพร้าว.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคนโลยี. (2559). หนังสือรายวิชาเพิ่มเติมคณิตศาสตร์ เล่ม 3 ชั้นมัธยมศึกษาปีที่ 4-6 กลุ่มสาระการเรียนรู้คณิตศาสตร์ ตามหลักสูตรแกนกล่างการศึกษาชั้นพื้นฐาน พุทธศักราช 2551. กรุงเทพมหานคระ โรงพิมพ์ สกสค. ลาดพร้าว.