ปริมาณทางฟิสิกส์ หมายถึง สิ่งที่เราสามารถวัดค่า บอกค่าได้แน่นอน และใช้แสดงกฎเกณฑ์ต่าง ๆ ได้ซึ่งความหมายในทางฟิสิกส์อาจจะแตกต่างไปจากความหมายที่เราใช้อยู่ในชีวิตประจำวันปริมาณในทางฟิสิกส์แบ่งได้เป็น 2 พวก คือ  ปริมาณหลักมูลหรือปริมาณมูลฐาน (Fundamental Quantities)  และปริมาณอนุพัทธ์ (Derived  Quantities)

ภาพที่ 1 ตลับเมตร เครื่องมือที่ใช้ในการวัด
ที่มา: https://pixabay.com , OpenClipart-Vectors

1. ปริมาณหลักมูลหรือปริมาณมูลฐาน หมายถึง ปริมาณเบื้องต้นที่จำเป็นต่อการอธิบายปรากฏการณ์ทางฟิสิกส์ ปริมาณหลักมูลหรือปริมาณมูลฐาน มีทั้งหมด 7 ปริมาณ คือ

2. ความยาว (Length)                       

3. มวลสาร (Mass)

4. เวลา (Time)                             

5. กระแสไฟฟ้า (Electric Current)

6. อุณหภูมิทางเทอร์โมไดนามิกส์ (Thermodynamic Temperature)

7. ความเข้มของการส่องสว่าง (Luminous intensity)

8. ปริมาณของสสาร (Amount of Substance)

9. ปริมาณอนุพัทธ์ หมายถึง ปริมาณที่เกิดจากปริมาณหลักมูลหลาย ๆ ปริมาณมาประกอบกัน ทั้งนี้แล้วแต่ความสัมพันธ์ตามความหมายของปริมาณนั้น ๆ เช่น แรงเป็นปริมาณอนุพัทธ์ที่เกิดจากความสัมพันธ์ของปริมาณหลักมูล แต่ มวล ความยาว และเวลา หรือความเร็วเป็นปริมาณอนุพันธ์ที่เกิดจากความสัมพัทธ์ของปริมาณหลักมูล คือ ความยาว และเวลา ปริมาณอื่น ๆ ที่นอกเหนือจากปริมาณหลักมูลทั้ง 7 ปริมาณ ถือว่าเป็น ปริมาณอนุพันธ์ทั้งสิ้น

ตัวอย่างที่ 1  ข้อใดเป็นปริมาณหลักมูล

1. ความยาว 2. เวลา             3. มวล           4. ถูกทั้งข้อ 1  2  และ 3

เฉลย ข้อ  4 เพราะ ความยาว เวลา และมวลเป็นปริมาณหลักมูลหรือปริมาณมูลฐาน

ตัวอย่างที่ 2 เครื่องมือที่ใช้วัดกระแสไฟฟ้าคือข้อใด

1. โวลต์มิเตอร์ 2. วัตต์มิเตอร์      3. แอมมิเตอร์      4. โอห์มมิเตอร์

เฉลย  ข้อ 3 เพราะแอมมิเตอร์คือมือวัดปริมาณกระแสไฟฟ้า

ตัวอย่างที่ 3 ปริมาณใดที่มีหน่วยเป็นหน่วยอนุพัทธ์

1. ความถี่ 2. แรง           3. พลังงาน        4. ถูกทุกข้อ

เฉลย ข้อ 4 เพราะทุกปริมาณเป็นปริมาณอนุพัทธ์

        หน่วย (Unit) แต่เดิมหน่วยที่ใช้ในการวัดปริมาณต่าง ๆ ใช้อยู่ด้วยกันหลายระบบที่ใช้กันแพร่หลาย คือ ระบบอังกฤษและเมตริกของฝรั่งเศส แต่เนื่องจากระบบอังกฤษไม่สะดวกมีความยุ่งยากในการตัดทอนหรือการกระจายหน่วย ปัจจุบันจึงนิยมใช้หน่วยตามข้อเสนอขององค์การระหว่างประเทศว่าด้วยหน่วยมาตรฐานเรียกว่า ระบบหน่วยระหว่างชาติ (International System of Units) หรือเรียกโดยย่อว่า หน่วยในระบบ SI

 หน่วยมาตรฐานในระบบ SI ที่ใช้วัดปริมาณต่าง ๆ

1. ความยาว    หน่วยมาตรฐานที่ใช้  เมตร  (metre)  สัญลักษณ์ m
2. มวล   หน่วยมาตรฐานที่ใช้  กิโลกรัม (kilogram)  สัญลักษณ์ Km
3. เวลา         หน่วยมาตรฐานที่ใช้   วินาที  second)  สัญลักษณ์ S
4. กระแสไฟฟ้า หน่วยมาตรฐานที่ใช้  แอมแปร์(Ampere)  สัญลักษณ์ A
5. อุณหภูมิ  หน่วยมาตรฐานที่ใช้   เคลวิน (Kelvin)  สัญลักษณ์ K
6. ความเข้มของการส่องสว่าง  หน่วยมาตรฐานที่ใช้  แคนเดลา (Candela)  สัญลักษณ์  cd
7. ปริมาณของสสาร  หน่วยมาตรฐานที่ใช้  โมล   (mole)  สัญลักษณ์  mol

หน่วยมาตรฐานในระบบ SI ของปริมาณอนุพัทธ์ที่ควรทราบ

1. พื้นที่         หน่วยมาตรฐานที่ใช้  ตารางเมตร
2. ปริมาตร        หน่วยมาตรฐานที่ใช้  ลูกบาศก์เมตร
3. ความเร็ว       หน่วยมาตรฐานที่ใช้  เมตรต่อวินาที
4. อัตราเร็ว       หน่วยมาตรฐานที่ใช้  เมตรต่อวินาที
5. ความเร่ง หน่วยมาตรฐานที่ใช้  เมตรต่อวินาที²
6. แรง            หน่วยมาตรฐานที่ใช้  นิวตัน
7. โมเมนต์        หน่วยมาตรฐานที่ใช้  นิวตัน เมตร
8. โมเมนต์ตัม     หน่วยมาตรฐานที่ใช้  กิโลกรัม.เมตรต่อวินาที
9. งาน หน่วยมาตรฐานที่ใช้  จูล
10. กำลัง หน่วยมาตรฐานที่ใช้  วัตต์
11. ประจุไฟฟ้า หน่วยมาตรฐานที่ใช้  คูลอมบ์
12. ความหนาแน่น หน่วยมาตรฐานที่ใช้ กิโลกรัมต่อลกบาศก์เมตร
13. ความดัน     หน่วยมาตรฐานที่ใช้  นิวตันต่อตารางเมตร

ตารางที่ 1 มาตราการเทียบหน่วยในระบบ SI

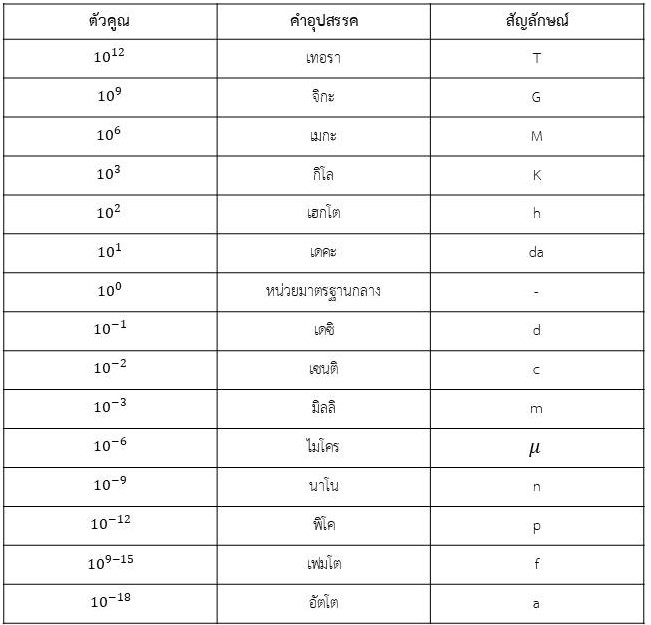
หลักการเปลี่ยนหน่วยระบบ SI

1. เปลี่ยนจากหน่วยใหญ่เป็นหน่วยเล็กคูณด้วย 10^x (10 กำลังเต็มบวก)
2. เปลี่ยนจากหน่วยเล็กเป็นหน่วยใหญ่คูณด้วย 10^-x (10 กำลังเป็นลบ)
3. x คือระยะห่างของเลขยกกำลังของหน่วยนั้น ๆ เช่น ถ้าต้องการเปลี่ยนหน่วยระหว่างหน่วย

              กิโล กับ ไมโคร x =6-(-3) = 9

(กำลังของหน่วยใหญ่ลบด้วยกำลังของหน่วยเล็ก) ดังนั้นถ้าจะเปลี่ยนหน่วยกิโลให้เป็นไมโคร (ใหญ่ไปเป็นเล็ก) คูณด้วย 10⁹ ถ้าจะเปลี่ยนหน่วยไมโครให้เป็นหน่วยกิโล (เล็กไปเป็นใหญ่) คูณด้วย 10^-9

ตัวอย่างที่ 1  จงเปลี่ยน 1.5 กิโลเมตร ให้เป็น ไมโครเมตร

         750 นาโนเมตร ให้เป็น เมกะเมตร

         25 เซนติเมตร ให้เป็น กิโลเมตร

หลักการคิด

         เปลี่ยน 1.5 กิโลเมตร ให้เป็น ไมโครเมตร เป็นการเปลี่ยนจากหน่วยใหญ่ไปหน่วยเล็ก คูณด้วย 10^x

                         X = 3 – (-6) = 9

 ดังนั้น 1.5 กิโลเมตร เท่ากับ 1.5 x 10⁹ นาโนเมตร

         เปลี่ยน 750 นาโนเมตร ให้เป็น เมกะเมตร เป็นการเปลี่ยนจากหน่วยเล็กไปหน่วยใหญ่ คูณด้วย 10^-x

                         X = 6- (-9) = 15

          (ค่าระยะห่าง x  เท่ากับกำลังหน่วยใหญ่ลบด้วยกำลังหน่วยเล็กเสมอ)

ดังนั้น 750 นาโนเมตร เท่ากับ 750 x 10^-15 เมกะเมตร

         เปลี่ยน 25 เซนติเมตร ให้เป็น กิโลเมตร เป็นการเปลี่ยนจากหน่วยเล็กไปหน่วยใหญ่ คูณด้วย 10^-x

X = 3 – (-2) = 5

ดังนั้น 25 เซนติเมตร เท่ากับ 25 x 10⁵ กิโลเมตร

ตัวอย่างที่ 2 จงเปลี่ยนความเร็วแสง 3 x 10¹¹ ไมโครเมตรต่อมิลลิวินาที ให้เป็น เมตรต่อวินาที

วิธีทำ  3 x 10¹¹ ไมโครเมตร/มิลลิวินาที  = (3 x 10¹¹ x 10^-6)/10^-3  เมตรต่อวินาที

                                                 = 3 x 10⁸ เมตรต่อวินาที

ตัวอย่างที่ 3 จงเปลี่ยน 2.5 ไมโครวัตต์ต่อตารางกิโลเมตร ให้เป็น เมกะวัตต์ต่อตารางเซนติเมตร

วิธีทำ  2.5 ไมโครวัตต์/ตารางกิโลเมตร = (2.5 x 10¹²)/(10⁵ x 10⁵) เมกะวัตต์ต่อตารางเซนติเมตร

                                               = 2.5 x 10² เมกะวัตต์ต่อตารางเซนติเมตร

ตัวอย่างที่ 4 จงเปลี่ยนค่าความหนาแน่น 500 กิโลกรัมต่อลูกบาศก์เมตร ให้เป็นกรัมต่อลูกบาศก์เซนติเมตร

วิธีทำ  500  กิโลกรัมต่อลูกบาศก์เมตร  = (500 x 10³)/(10² x 10² x 10²) กรัมต่อลูกบาศก์เซนติเมตร

                                                = 0.5 กรัมต่อลูกบาศก์เซนติเมตร

แหล่งที่มา

จรัญ  บุระตะ. (2555). ฟิสิกส์ เล่ม 1 ม. 4-6. กรุงเทพฯ:นิพนธ์.

พงษ์ศักดิ์  ชินนาบุญ. (2554). ฟิสิกส์  เล่ม 1. กรุงเทพฯ:วิทยพัฒน์.

Panuwat  songpray  . (มมป). เครื่องมือวัด . สืบค้นเมื่อ 15 สิงหาคม 2562,                             

จาก https://sites.google.com/site/measuringtoolssci/tap-rule

           ในการทดลองครั้งหนึ่งวัดมวลของวัตถุได้ 5.3 กิโลกรัม และวัดปริมาตรได้ 1.67  ลูกบาศก์เมตร  เมื่อต้องการทราบความหนาแน่นของวัตถุจะคำนวณได้ดังนี้

                   ความหนาแน่น = มวล/ปริมาตร

                                    = 5.3 กิโลกรัม /1.67 ลูกบาศก์เมตร

                                    = 3.173652695 กิโลกรัมต่อลูกบาศก์เมตร

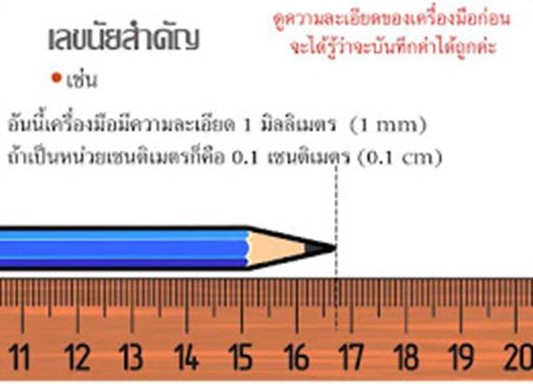
ภาพที่ 1 การอ่านค่าเลข
ที่มา: https://pixabay.com , qimono

         จะเห็นได้ว่าผลหารที่ได้จากการคำนวณด้วยเครื่องคิดเลข ค่าความคลาดเคลื่อนในจำนวนวัดของมวลและปริมาตรของวัตถุได้ถูกส่งต่อและขยายตัวผ่านการคำนวณทางคณิตศาสตร์ไปยังผลการคำนวณความหนาแน่น คำถามที่สำคัญคือ ควรบันทึกผลการคำนวณความหนาแน่นด้วยตัวเลขหรือจำนวนที่มีทศนิยมกี่ตำแหน่ง

         ความคลาดเคลื่อนของผลการคำนวณจากกระบวนการทางคณิตศาสตร์สามารถหาได้ด้วยวิธีทางสถิติ แต่วิธีที่ง่ายกว่าและใช้กันอย่างแพร่หลายในการประมาณความคลาดเคลื่อนนี้ คือ การพิจารณาจากเลขนัยสำคัญ (significant figures หรือย่อเป็น sf)  ซึ่งต่อไปนี้จะกล่าวถึงเลขนัยสำคัญก่อนแล้วจึงจะใช้เลขนัยสำคัญในการพิจารณาผลการคำนวณ

         เลขนัยสำคัญ คือ ตัวเลขที่ได้จากการวัดหรือจำนวนวัดนั่นเอง เช่น การวัดความยาวแท่งวัตถุด้วยไม้บรรทัดที่มีความละเอียดแตกต่างกัน โดยสามารถวัดได้ค่าดังนี้ 85 เซนติเมตร, 85.2  เซนติเมตร,  และ 85.23 เซนติเมตร ตามลำดับ  ซึ่งจะเห็นได้ว่ายิ่งตัวเลขในเลขนัยสำคัญมีจำนวนมากขึ้น ผลการวัดย่อมมีความถูกต้องมากยิ่งขึ้นด้วย ดังนั้น สิ่งแรกที่ต้องการทราบเมื่อพิจารณาเลขนัยสำคัญคือจำนวนตัวเลขที่มีนัยสำคัญ ในส่วนต่อไปนี้เป็นเกณฑ์ในการนับจำนวนตัวเลขที่มีนัยสำคัญ

1. เลข 1 ถึง 9 เป็นตัวเลขที่อ่านได้จากอุปกรณ์เครื่องมือวัด ดังนั้น ให้นับเป็นเลขนัยสำคัญทุกตัว เช่น 2345  มีเลขนัยสำคัญ 4 ตัว คือ เลข 2, 3, 4 และ 5

       13.3   มีเลขนัยสำคัญ 3 ตัว คือ เลข 1, 3, 3

2. เลข 0 มีเกณฑ์ในการนับเป็นเลขนัยสำคัญ คือ

              2.1 เลข 0 ที่อยู่ด้านหน้าเลขอื่น ๆ เช่น 0.00154 ไม่นับเป็นเลขที่มีนัยสำคัญ เนื่องจากเลขศูนย์เหล่านี้เป็นเพียงการกำหนดตำแหน่งของทศนิยม ไม่เกี่ยวข้องใด ๆกับความถูกต้อง

              ของ จำนวนวัด ดังนั้น 0.00154 มีเลขนัยสำคัญ 3 ตัว คือ เลข 1, 5  และ 4

              2.2 เลข 0 ที่อยู่ระหว่างตัวเลขอื่น ๆ ให้นับเป็นเลขที่มีนัยสำคัญทุกตัว เนื่องจากเป็นตัวเลขที่อ่านได้จากอุปกรณ์วัด เช่น   1044  มีเลขนัยสำคัญ 4 ตัว คือ เลข 1, 0, 4 และ 4

              2.3  เลข 0  ที่อยู่ด้านหลังเลขอื่น ๆ และอยู่หลังจุดทศนิยมให้นับเป็นเลขที่มีนัยสำคัญทุกตัว เนื่องจากเป็นตัวเลขที่อ่านได้จากอุปกรณ์วัด เช่น 0.4500  มีเลขนัยสำคัญ 4 ตัว คือ

              เลข 4,5,0 และ 0 โดยเลข 0 ตัวแรกไม่ใช่เลขนัยสำคัญ 0.000320 มีเลขนัยสำคัญ 3 ตัว คือ เลข 3, 2  และ 0 โดยเลข 0 จำนวนสามตัวที่อยู่ด้านหน้าไม่ใช่เลขนัยสำคัญ  150.0

              มีเลขนัยสำคัญ 4 ตัว คือ เลข 1, 5, 0 และ 0

3. เลข 0 ที่อยู่หลังเลขอื่น ๆ ในรูปของจำนวนเต็ม เช่น 1500  อาจจะเป็นเลขที่มีนัยสำคัญหรือไม่มีก็ได้ สาเหตุเนื่องจากในกรณีนี้เลข 0 จำนวน 2 ตัว อาจจะเป็นตัวเลขที่อ่านได้จากปกรณ์วัด หรือเป็นเพียงตัวเลขที่เติมเข้าไปเพื่อให้จำนวนวัดมีหลัก 10 กับหลักหน่วยครบเท่านั้น ดังนั้นเพื่อไม่ให้เกิดความคลุมเครือ จึงนิยมเขียนในรูปของ A x 10ⁿ โดย 1 ≤ A< 10  และ n เป็นจำนวนเต็ม เรียกรูปแบบการเขียนตัวเลขเช่นนี้ว่าสัญกรณ์วิทยาศาสตร์ (scientific notation) ยกตัวอย่างเช่น หากมีเพียงเลข 1 กับ 5  เท่านั้นที่เป็นเลขนัยสำคัญตัวเลข 1500 ควรเขียนเป็น 1.5 x 10³ ซึ่งแสดงเลขนัยสำคัญเพียง 2 ตัว หากเลข 0 ตัวแรกเป็นเลขที่มีนัยสำคัญด้วย ซึ่งหมายถึง 1500  มีเลขนัยสำคัญ 3 ตัว จะเขียนได้เป็น 1.50 x 10³ และหากเลข 0  ทั้ง 2 ตัวเป็นเลขที่มีนัยสำคัญ จะเขียนได้เป็น 1.500 x 10⁴ ซึ่งมีเลขนัยสำคัญ 4 ตัว ข้อสังเกตคือเลข 1 กับ 5 เป็นเลขที่มีนัยสำคัญอย่างแน่นอน และไม่ต้องพิจารณาเลขนัยสำคัญจากเลขฐาน 10  ใน 10ⁿ ดังนั้นเราสามารถสรุปได้ดังนี้  ตัวเลขทุกตัวยกเว้น 0 เป็นเลขนัยสำคัญอย่างแน่นอน ส่วนเลข 0 ต้องพิจารณาตามเกณฑ์ที่ผ่านมา

การคูณและการหารเลขนัยสำคัญ

        การคูณจำนวน 12.3 x 3.1416  ด้วยเครื่องคิดเลขซึ่งเป็นการคำนวณทางคณิตศาสตร์ จะได้ผลการคำนวณเท่ากับ 38.6418  หารคูณเช่นนี้มีการรวมตัวเลขที่ไม่มีนัยสำคัญไว้ในผลการคำนวณด้วย ซึ่งผลการคำนวณจากการคูณจะมีเลขนัยสำคัญ 3 ตัว เท่ากับจำนวนเลขนัยสำคัญของ 12.3 ซึ่งเป็นจำนวนเลขนัยสำคัญที่น้อยที่สุดของจำนวนที่นำมาคูณกัน ดังนั้นจึงสรุปได้ว่า

          ผลลัพธ์ที่ได้จากการคูณและการหารจะเท่ากับจำนวนเลขนัยสำคัญที่น้อยที่สุด

การบวกและการลบเลขนัยสำคัญ

      การบวกจำนวน 3.17:785 + 2.32 + 4.8  ด้วยเครื่องคิดเลขจะได้ผลการคำนวณเท่ากับ10.2985  ซึ่งเป็นการบวกที่มีการรวมตัวเลขที่ไม่มีเลขนัยสำคัญไว้ในผลการคำนวณ โดยผลการคำนวณจากการบวกจะมีเลขนัยสำคัญ 3 ตัว เท่ากับจำนวนเลขนัยสำคัญของ 10.3 ซึ่งเป็นผลการคำนวณที่มีจำนวนทศนิยม 1 ตำแหน่งเท่ากับจำนวนทศนิยมใน 4.8  ซึ่งเป็นจำนวนที่มีตำแหน่งทศนิยมน้อยที่สุดในจำนวนที่นำมาบวกกัน ดังนั้นเงื่อนไขในการพิจารณาผลการคำนวณจากการบวกและการลบจึงอยู่ที่จำนวนตำแหน่งทศนิยม ไม่ใช่จำนวนเลขนัยสำคัญ ดังนั้น จึงสรุปได้ว่า

       ผลลัพธ์ที่ได้จะมีจำนวนตัวเลขหลังจุดทศนิยมเท่ากับจำนวนตัวเลขหลังจุดทศนิยมที่น้อยที่สุดของปริมาณที่นำมาบวก ลบ กัน

แหล่งที่มา

คณาจารย์แม็ค. (2551). ฟิสิกส์ ม.4. กรุงเทพฯ:แม็ค.

พงษ์ศักดิ์  ชินนาบุญ. (2554). ฟิสิกส์  เล่ม 1. กรุงเทพฯ:วิทยพัฒน์.

มณิศา  ชื่นจิต. (2558).  เลขนัยสำคัญ.  สืบค้นเมื่อ 15 สิงหาคม 2562,จาก http://thn238299physics.blogspot.com/2015/08/16.html