เซตและการดำเนินการของเซต
เซตพื้นฐาน
เซตเป็นหัวข้อที่มีความสำคัญและแทรกอยู่ในเนื้อหาของคณิตศาสตร์แทบทุกส่วน เราใช้เซตในการรวบรวมสิ่งต่าง ๆ ไม่ว่าจะเป็น ค่าตัวเลข ตัวแปร ที่มีคุณสมบัติเหมือนกันไว้ด้วยกันเป็นประโยชน์ต่อการจำแนกประเภทของสิ่งต่าง ๆ ออกเป็นกลุ่ม
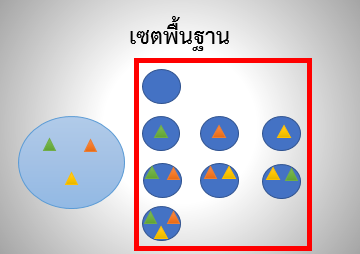
ภาพที่ 1 สับเซตทั้งหมดของเซตที่มีสมาชิก 3 ตัว
ที่มา วีระ ยุคุณธร
การกำหนดเซต
การรวบรวมสิ่งต่าง ๆเข้าด้วยกันเรียกว่าเซต สิ่งที่อยู่ในเซตเราเรียกว่าสมาชิกเช่นเซต A ประกอบด้วยสมาชิก 5 ตัวได้แก่ a, e, i, o, u กล่าวได้ว่า a เป็นสมาชิกของเซต A แต่ b ไม่เป็นสมาชิกของเซต A ประโยคภาษาข้างต้นสามารถเปลี่ยนเป็นสัญลักษณ์ทางคณิตศาสตร์ได้ดังนี้
ตารางที่ 1 แสดงการแทนข้อความการเป็นสมาชิกของเซตแบบแจงแจกสมาชิกด้วยสัญลักษณ์

การเขียนเซตในตารางที่ 1 เราเรียกว่าการกำหนดเซตแบบแจกแจงสมาชิกนิยมใช้เมื่อเราต้องการระบุสมาชิกของเซต แต่บางกรณีที่เราไม่ต้องการแจกแจงสมาชิกหรือไม่สามารถระบุสมาชิกที่แน่นอนได้ จึงมีวิธีการกำหนดเซตในลักษณะของการบอกคุณสมบัติมีหลักการดังนี้ กำหนดให้ A เป็นเซตที่มีคุณสมบัติ P นั้นคือสำหรับ x ใดๆที่เป็นสมาชิกใด ๆของ A แล้ว x จะต้องมีคุณสมบัติ P เขียนแทนด้วยสัญลักษณ์ตัวตารางต่อไปนี้
ตารางที่ 2 แสดงการแทนข้อความการเป็นสมาชิกของเซตแบบมีเงื่อนไขด้วยสัญลักษณ์

จากตัวอย่างข้างต้นเราสามารถกล่าวได้ว่า A เป็นเซตที่รวบรวมอักษรสระในภาษาอังกฤษกล่าวคือ ถ้า x เป็นสมาชิกใด ๆของเซต A แล้ว x จะต้องเป็นตัวอักษรภาษาอังกฤษ ในขณะเดียวกันหากไม่ใช่สมาชิกของเซต A ย่อมไม่ใช่ตัวอักษรในภาษาอังกฤษการใช้สัญลักษณ์ในตารางที่ 2 สื่อความหมายดังตารางต่อไปนี้
ตารางที่ 3 ตัวอย่างการแปรความหมายสัญลักษณ์การเป็นสมาชิกของเซต

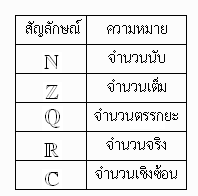
ในบางครั้งจะมีการกำหนดสัญลักษณ์ของเซตที่ถูกกล่าวถึงอยู่บ่อยครั้งเช่นในระบบจำนวนเรากำหนดสัญลักษณ์ของจำนวนดังนี้
ตารางที่ 4 สัญลักษณ์ของเซตในระบบจำนวน
ขนาดของเซต
การรวบรวมวัตถุต่าง ๆเป็นเซต ถ้าจำนวนสมาชิกที่อยู่ในเซตมีจำนวนมากย่อมส่งผลให้เซตมีขนาดใหญ่ตามไปด้วย ดังนั้นคุณสมบัติพื้นฐานในการวัดขนาดของเซตคือ เซตนั้นจะต้องเป็นเซตที่สามารถนับจำนวนสมาชิกได้เรียกว่า เซตนับได้ พิจารณาเซตต่อไปนี้ กำหนดให้ A = {x, x เป็นจำนวนเต็มที่อยู่ระหว่าง -10 และ 10} และ B = {x, x เป็นจำนวนเต็มที่มากกว่า 10} จะเห็นว่าทั้ง A และ B สามารถเขียนแจงแจงสมาชิกได้ดังนี้ A = { -10,-9,-8,…,8,9,10 } และ B = { 10, 11 ,12, …} จะเห็นว่า A และ B เป็นเซตนับได้โดยที่ A มีสมาชิก 20 ตัว แต่ B มีจำนวนสมาชิกเป็นอนันต์ สำหรับเซตที่ไม่มีสมาชิกเรียกว่า เซตว่าง กล่าวได้ว่าเซตว่างเป็นเซตที่มีจำนวนสมาชิก 0 ตัว ดังนั้นเซตนับได้ยังสามารถจำแนกได้เป็นอีกสองประเภทคือ เซตที่มีจำนวนสมาชิกเป็นจำนวนเต็มบวกหรือศูนย์เรียกว่า เซตจำกัด และเซตที่มีสมาชิกมากมายนับไม่ถ้วนเรียกว่าเซตอนันต์ ส่วนการใช้สัญลักษณ์บอกขนาดของเซตแสดงดังตารางต่อไปนี้
ตารางที่ 5 ตัวอย่างการแปรความหมายสัญลักษณ์จำนวนสมาชิกของเซต

ความสัมพันธ์ระหว่างเซตสองเซต
การพิจารณาขนาดและสมาชิกของเซต 2 เซตทำให้เราสามารถบอกความสัมพันธ์ระหว่างเซตทั้งสองเซตได้ตัวอย่างเช่นกำหนดให้ A = {x, x เป็นจำนวนเต็มบวกที่มีค่าไม่เกิน 10 และ 2หารได้ลงตัว} และ B = { x, x=2k เมื่อ k = 1,2,3,4,5 } จะเห็นว่าเซต A และ เซต B ถูกกำหนดด้วยภาษาที่แตกต่างกันแต่เมื่อพิจารณาสมาชิกแล้วจะพบว่าทั้งเซต A และ เซต B เขียนแจงแจงสมาชิกได้คือ { 2, 4, 6, 8, 10 } นั้นหมายความว่า เซต A และ เซต B เป็นเซตเดียวกันนิยามด้วยการเท่ากันของเซตดังนี้
A = B ก็ต่อเมื่อ สามาชิกทุกตัวของเซต A เป็นสมาขิกของเซต B และ สมาชิกทุกตัวของเซต B เป็นสมาชิกของเซต A
สังเกตได้ว่า A และ B จะต้องมีจำนวนสมาชิกเท่ากัน และเป็นชุดเดียวกันแต่ถ้าหาก A และ B มีจำนวนสมาชิกเท่ากันแต่มีสมาชิกในเซตแตกต่างกันแล้วจะกล่าวว่า เซต A และ เซต B เป็นเซตที่เทียบเท่ากันนิยามดังนี้
A ~ B ก็ต่อเมื่อ n(A) = n(B)
กำหนดให้ A = { x, x เป็นอักษรสระของภาษาอังกฤษ } และ B = { 1, 2, 3, 4, 5 } จะเห็นว่า n(A) = 5 = n(B) ดังนั้น A และ B เป็นเซตที่เทียบเท่ากัน สังเกตว่าเซตจำกัดที่มีสมาขิก k ตัวเทียบเท่ากับเซต {1,2,3,…,k } เสมอ
ในกรณีที่สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B แต่ n(A) น้อยกว่า n(B) เรากล่าวว่า เซต A เซตย่อยแท้ของเซต B แต่ถ้า n(A) น้อยกว่าหรือเท่ากับ n(B) จะกล่าวว่า เซต A เป็นเซตย่อยของเซต B ตัวอย่างเช่นถ้ากำหนดให้ B = { 1,2,3,4,5 } ถ้า A = { 1,4,5 } จะเห็นว่าสมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และ เซต A มีขนาดเล็กกว่า เซต B สรุปได้ว่า A เป็นเซตย่อยแท้ของเซต B แต่ถ้ากำหนดให้ A ={ 1,3,9 } จะเห็นว่ามีสมาชิกบางตัวของเซต A ไม่ใช่สมาชิกในเซต B เราสรุปได้ว่า A ไม่เป็นเซตย่อยของเซต B
เราให้นิยามความสัมพันธ์เชิงเซตย่อยของเซตสองเซตได้ดังนี้
A เป็นเซตย่อยของ B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B
A เป็นเซตย่อยแท้ของ B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และ n(A) ไม่เท่ากับ n(B)
ตัวอย่างการหาเซตย่อยของ A = { { }, { { } } ,{ { }, {{ }} } } เพื่อความสะดวกผู้เขียนจะใช้ e แทนเซตว่างจะได้
A = { e, {e}, {e,{e}} } พบว่า A ประกอบด้วยสมาชิก 3 ตัวคือ e, {e} และ {e, {e}} พิจารณาเซตย่อยคือเซตที่มีสมาขิกน้อยกว่า 3 ตัวได้แก่ เซตที่มีสมาชิก 0 ตัว 1 ตัว 2 ตัว และ 3 ตัวตามลำดับ พิจารณา
เซตที่มีสมาชิก 0 ตัว e มีจำนวน 1 เซต
เซตที่มีสมาชิก 1 ตัว { e } , { {e} }, { { e, {e} } } มีจำนวน 3 เซต
เซตที่มีสมาชิก 2 ตัว { e , {e} }, { e, {e, {e}} }, { {e}, {e, {e}} } มีจำนวน 3 เซต
เซตที่มีสมาชิก 3 ตัว { e, {e}, {e,{e}} } มีจำนวน 1 เซต
จะเห็นว่าเซตย่อยของเซตที่มีจำนวนสมาชิกเท่ากับ 3 มี 8 เซต แต่หากพิจารณาเซตย่อยแท้จะมีเพียงเซต 7 เซต (นับเฉพาะเซตที่มีสมาชิกน้อยกว่า 3} นอกจากนี้สังเกตได้ว่าเมื่อพิจารณาถึงเซตย่อยย่อมมีเซตย่อยที่แจ่มชัดอยู่ 2 เซตย่อยเสมอคือเซตว่างและเซตนั้นนั่นเอง หากเรารวมรวมเซตย่อยทั้ง 8 เซตเข้าด้วยกันเป็นเซตใหม่เราเรียกว่า เพาเวอร์เซต นั้นคือ เพาเวอร์เซตของเซตของเซต A คือ เซตของเซตย่อยของเซต A
P(A) = { e, { e } , { {e} }, { { e, {e} } }, { e , {e} }, { e, {e, {e}} }, { {e}, {e, {e}} }, { e, {e}, {e,{e}} } }
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา
การดำเนินการของเซต
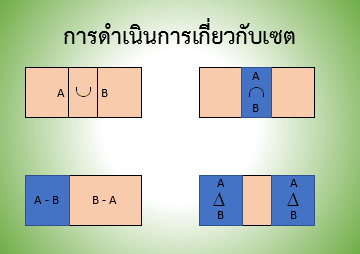
ภาพผังเวนน์ออยเลอร์แสดงผลการดำเนินการระหว่างเซต A และ B
ที่มา วีระ ยุคุณธร
เมื่อเราทำการจำแนกสิ่งต่าง ๆออกเป็นกลุ่ม หากเราพิจารณากลุ่ม 2 กลุ่มแล้วนำมารวมกันจะได้กลุ่มใหม่ที่มีสมาชิกจากทั้งสองกลุ่ม ในขณะเดียวกันหากเรามองหาส่วนที่ซ้ำกันระหว่างกลุ่มสองกลุ่มเราจะได้กลุ่มใหม่ที่มีขนาดเล็กกว่ากลุ่มเดิมและสมาชิกในกลุ่มใหม่เป็นสมาชิกของกลุ่มเดิมทั้งสองกลุ่ม การดำเนินการทั้งสองแบบนี้เป็นพื้นฐานของการดำเนินการเรื่องเซตเราเรียกการรวมเซตสองเซตเข้าด้วยกันว่าผลผนวก และเรียกการเลือกส่วนที่ซ้ำกันระหว่างเซตสองเซตว่าผลตัด
ผลผนวก
กำหนดให้ A = { 1, 3, 5 } และ B = { 2, 4, 6 } หากนำสมาชิกของเซต A และ เซต B มารวมกันจะได้เซตใหม่ซึ่งเป็นผลผนวกของ เซต A และ เซต B เขียนแทนด้วย A U B = { 1, 2, 3, 4, 5, 6 } ถ้ากำหนดให้ C = {2,3,5} พิจารณา A U C = {1, 3, 5, 2, 3, 5} = { 1, 2, 3, 5 } จากทั้งสองกรณีจะเห็นว่าสมาชิกของผลผนวกจะต้องเป็นสมาชิกของเซตใดเซตหนึ่ง หรือ อาจจะเป็นสมาชิกของเซตทั้งสองเซตก็ได้ นิยามของผลผนวกจึงกำหนดได้ดังนี้
A U B = { x, x เป็นสมาชิกของเซต A หรือ x เป็นสมาชิกของเซต B }
คุณสมบัติของผลผนวก
-
A U A = A การนำเซตเดียวกับมารวมกันย่อมได้เซตเดิม
-
A U ( B U C ) = ( A U B) U C การนำเซต B รวมกับเซต C จากนั้นนำไปรวมกันเซต A จะได้เซตเดียวกันกับการรวมเซต A และ เซต B แล้วไปรวมกับเซต C
-
A U B = B U A การนำเซต A ไปรวมกับเซต B เป็นเซตเดียวกันกับ การนำเซต B ไปรวมกันเซต A
ผลตัด
จากการกำหนดให้ A = { 1, 3, 5 } B = { 2, 4, 6 } และ C = {2,3,5} เมื่อนำสมาชิกที่ซ้ำกันทั้งหมดระหว่างเซต A และ เซต C มาสร้างเป็นเซตใหม่เรียกเซตนี้ว่าผลตัดของ เซต A และ เซต C เขียนแทนด้วย A ∩ C = { 3, 5 } ขณะเดียวกัน A ∩ B = { } เนื่องจากไม่มีสมาชิกร่วมกันเลย ในกรณีแรกจะเห็นว่าสมาชิกของผลตัดจะต้องเป็นสมาชิกของเซตทั้งสองเซตดังนิยามต่อไปนี้
A ∩ B = { x, x เป็นสมาชิกของเซต A และ x เป็นสมาชิกของเซต B }
คุณสมบัติของผลผนวก
-
A ∩ A = A การเลือกส่วนที่ซ้ำกันของเซตเดียวกันย่อมได้เซตเดิม
-
A ∩ ( B ∩ C ) = ( A ∩ B) ∩ C การเลือกส่วนที่ซ้ำกันระหว่างเซต B กับเซต C จากนั้นนำไปเลือกส่วนที่ซ้ำกันกับเซต A จะได้เซตเดียวกันกับการเลือกส่วนที่ซ้ำกันระหว่างเซต A และ เซต B แล้วเลือกส่วนที่ซ้ำกันกับเซต C
-
A ∩ B = B ∩ A การเลือกส่วนที่ซ้ำกันระหว่างเซต A กับเซต B เป็นเซตเดียวกันกับ การเลือกส่วนที่ซ้ำกันของเซต B กับเซต A
พิจารณาการดำเนินการที่มีทั้งการรวมและการเลือก
- A U ( B ∩ C ) = ( A U B ) ∩ ( A U C )
ตัวอย่างเช่นกำหนดให้ A = { 1, 3, 5 } B = { 2, 4, 6 } และ C = {2,3,5}
( A U B ) ∩ ( A U C ) = { 1,2,3,4,5,6 } ∩ { 1,2,3,5 } = {1,2,3,5}
A U ( B ∩ C ) = { 1, 3, 5 } U { 2,3 } = {1,2,3,5}
- A ∩ ( B U C ) = ( A ∩ B ) U ( A ∩ C )
ตัวอย่างเช่นกำหนดให้ A = { 1, 3, 5 } B = { 2, 5, 6 } และ C = {2,3,5}
( A ∩ B ) U ( A ∩ C )= { 1,5 } ∩ { 5 } = { 5}
A U ( B ∩ C ) = { 1, 3, 5 } U { 5 } = { 5 }
ผลต่าง
เมื่อเซต A และ เซต B มีสมาชิกบางส่วนที่ซ้ำกันและเราต้องการนำสมาชิกของเซต A ที่ซ้ำกับเซต B ออกจะเห็นว่าเซตนั้นจะต้องเป็นเซตที่มีสมาชิกของเซต A และ ต้องไม่เป็นสมาชิกในเซต B เราเรียกเซตนี้ว่า ผลต่างของ A และ B นิยามได้ดังนี้
A – B = { x, x เป็นสมาชิกของเซต A แต่ x ไม่เป็นสมาชิกของเซต B }
นิยามข้างต้นเรากล่าวถึง x ไม่เป็นสมาชิกของเซต B เราสามารถรวบรวมสมาชิกทั้งหมดที่ไม่ใช้สมาชิกของเซตฺBและเรียกเซตนี้ว่าส่วนเติมเต็มของ B เขียนแทนด้วย BC นั้นคือ ถ้า x ไม่ใช่สมาชิกของเซต B แล้ว x จะต้องเป็นสมาชิกของ BC ดังนั้นนิยามของผลต่างสามารถเขียนในรูปของผลตัดได้ดังนี้
A – B = { x, x เป็นสมาชิกของเซต A แต่ x ไม่เป็นสมาชิกของเซต B }
A – B = { x, x เป็นสมาชิกของเซต A และ x เป็นสมาชิกของเซต BC }
A – B = A ∩ BC
ผลต่างสมมาตร
ผลตัดเป็นการดำเนินการโดยเลือกส่วนที่ซ้ำกันของเซตสองเซตแต่หากเราสนใจส่วนที่ไม่ซ้ำกันสามารถอธิบายได้ด้วยผลต่างสมมาตรของเซตสองเซตนั้นคือ
A Δ B = (A – B) U (B – A)
ตัวอย่างเช่นให้ A = { 1, 3, 5 } B = { 2, 5, 6 }
A Δ B = (A – B) U (B – A)
A Δ B = { 1,3 } U { 2,6 }
A Δ B = { 1,2,3,6 }
จะเห็นว่า 1, 2, 3 และ 6 เป็นสมาชิกที่อยู่ในเซต A หรือ เซต B เซตใดเซตหนึ่ง
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา
ผลคูณและผลแบ่งกั้นของเซต
ตัวดำเนินการพื้นฐานของเซตประกอบด้วยการรวมและการเลือก นำมาซึ่งผลการดำเนินการมากมายเช่นผลผนวก ผลตัด ผลต่าง ผลต่างสมมาตร ในหัวข้อนี้จะกล่าวถึงผลคูณของเซตที่ซึ่งเป็นการจับคู่ระหว่างเซตสองเซตอย่างมีลำดับ และเป็นบทนำไปสู่การศึกษาเรื่องความสัมพันธ์กับฟังก์ชัน และหัวข้อสุดท้ายของเรื่องเซตจะเป็นการศึกษาเกี่ยวกับผลแบ่งกั้นที่ถูกประยุกต์ใช้มากในการจัดการข้อมูลและระบบ
ภาพที่ 1 โครงสร้างระบบจำนวนจริง
ที่มา วีระ ยุคุณธร
ผลคูณของเซต
กำหนดให้ A = { a,b,c } และ B = { 1,2,3,4 } สังเกตว่าเซตสองเซตเป็นปริมาณสองชนิดที่แตกต่างกัน หากเราต้องการจับคู่สมาชิกระหว่างเซตสองเซตนี้และเขียนในรูปของคู่อันดับ (a,b) เมื่อ a และ b เป็นสมาชิกของเซต A และ B ตามลำดับจะได้
(a,1) (a,2) (a,3) (a,4)
(b,1) (b,2) (b,3) (b,4)
(c,1) (c,2) (c,3) (c,4)
เมื่อเรารวบรวมการจับคู่เหล่านี้เข้าเป็นเซตเราเรียกเซตใหม่ที่ได้นี้ว่าผลคูณคาร์ทีเซียนของ A และ B แทนด้วยA x B = { (a,1), (a,2),(a,3), (a,4), (b,1), (b,2), (b,3), (b,4), (c,1), (c,2), (c,3), (c,4) }
นิยามโดยทั่วไปได้ว่า A x B = { (a,b) , a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B }
แต่ถ้าหากเราพิจารณา B x A จะได้
(1,a) (2,a) (3,a) (4,a)
(1,b) (2,b) (3,b) (4,b)
(1,c) (2,c) (3,c) (4,c)
B x A = { (1,a), (2,a),(3,a), (4,a), (1,b), (2,b), (3,b), (4,b), (1,c), (2,c), (3,c), (4,c) }
จะว่า A x B ไม่เท่ากับ B x A แต่ n(A x B) เท่ากับ n(B x A) นิยามคำว่าคูณที่สมนัยกับการคูณของจำนวนจริงจึงหมายถึงการคูณของจำนวนสมาชิกตามกฏต่อไปนี้
n(A x B) = n(A) x n(B)
หากเราพิจารณาผลคูณของเซตมากกว่าหนึ่งเซต สมมติให้ A1, A2, A3, ...., Ak เป็นเซตใด ๆแล้ว
A1 x A2 x A3 x .... Ak = { (a1,a2,…,ak), an เป็นสมาชิกของ An สำหรับ n =1,2,3,…k }
เราเรียกสมาชิกในผลคูณว่าว่าเวกเตอร์เช่นตัวอย่าง กำหนดให้ B = { 0, 1 } จะได้ว่า B3 = B x B x B = { (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1) } ในทางคอมพิวเตอร์เราเรียกตัวอย่างข้างต้นว่าสายบิตนิยมเขียนเป็น 000 001 010 011 100 101 110 111 เมื่อแปลงจากเลขฐานสองเป็นเลขฐาน 10 จะได้ 0,1,2,…,7 ตามลำดับ
ผลแบ่งกั้น
ก่อนจะกล่าวถึงผลแบ่งกั้น ผู้เขียนจะยกตัวอย่างการแบ่งกั้นพื้นที่ทั่วไปก่อนเพื่อเป็นแนวทางในการนิยามผลแบ่งกันในเซต พิจารณารูปที่ 2
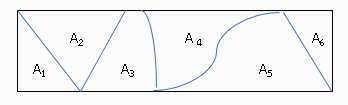
ภาพการแบ่งกั้นพื้นที่สี่เหลี่ยม A
จะเห็นว่ารูปสี่เหลี่ยม A ถูกแบ่งออกเป็น 6 ส่วนโดยที่แต่ละส่วนไม่มีส่วนที่ซ้ำกันเลยถ้าเรารวบรวม A1, A2, … , A6 เป็นเซตเราจะเรียกเซตนี้ว่าผลแบ่งกันของ A เรานิยามผลแบ่งกั้นของเซตจากข้อสังเกต 1. คือผลผนวกของสมาชิกในผลแบ่งกั้นจะต้องเป็นเซต A และ สมาชิกแต่ละคู่ของผลแบ่งกั้นจะต้องไม่มีส่วนที่ซ้ำกัน กำหนดด้วยนิยามในเชิงคณิตศาสตร์ได้ดังนี้
เราจะกล่าวว่า S = { A1, A2, … , An } เป็นผลแบ่งกั้นของเซต A ก็ต่อเมื่อ
- A1 U A2 U … U An = A
- A i ∩ A j = { } สำหรับ i ≠ j
ผลแบ่งกั้นถูกนำมาใช้เพื่อจำแนกประเภทของสิ่งต่าง ๆ หรือการจัดข้อมูลเป็นระดับชั้น ตัวอย่างเช่นหากเราพิจารณาประเภทของจำนวนเต็มเราสามารถแบ่งเซตของจำนวนเต็ม Z ออกได้เป็นหลายประเภทเช่น
- จำนวนเต็มบวก (Z+) จำนวนเต็มลบ (Z-) จำนวนเต็มศูนย์ (Z0) เนื่องจาก Z = Z+ U Z- U Z0 และ Z+ ∩ Z- = Z- ∩ Z0 = Z0 ∩ Z+ = { } นั้นคือ { Z+, Z-, Z0 } เป็นผลแบ่งกั้นของจำนวนเต็ม
- จำนวนคู่ ( E ) และจำนวนคี่ ( O ) เนื่องจาก Z = E U O และ E ∩ O = { } ดังนั้น { E , O } เป็นผลแบ่งกั้นของจำนวนเต็ม
- เศษเหลือ เช่นแบ่งตามเศษเหลือของ 5 จะได้ดังนี้
[0] = { …, -10, -5, 0, 5, 10, … }
[1] = { …, -9, -4, 1, 6, 11, … }
[2] = { …, -8, -3, 2, 7, 12, … }
[3] = { …, -7, -2, 3, 9, 13, … }
[4] = { …, -6, -1, 4, 9, 14, … }
จะเห็นได้โดยง่ายว่า { [0], [1], [2], [3], [4] } เป็นผลแบ่งกั้นของจำนวนเต็ม
ชุดข้อมูล (Data set) เป็นการเก็บข้อมูลเชิงตัวเลขหลายผลแบ่งกั้นเช่น
กำหนดให้เลข 2 หลักแรกหมายถึง ลำดับของผู้ถูกสำรวจ { 01, 02,…, 99}
กำหนดให้เลขหลักที่ 3 และ 4 แทนเพศ { 01 = ชาย, 02 = หญิง }
กำหนดให้เลข 2 หลักสุดท้ายหมายถึง คณะที่ศึกษา { 01=คณะวิทยาศาสตร์, 02 = คณะครุศาสตร์, 03 = คณะมนุษยศาสตร์, 04 = คณะวิทยาการจัดการ, 05 = คณะเทคโนโลยีอุตสาหกรรม}
หากเราต้องการเก็บข้อมูลของผู้ถูกสำรวจไว้เป็นความลับวิธีการหนึ่งคือเก็บข้อมูลในเชิงตัวเลขซึ่งจะมีเพียงผู้ที่รวบรวมข้อมูลเพื่อวิเคราะห์เท่านั้นที่สามารถอ่านข้อมูลได้ตัวอย่างเช่นปรากฏข้อมูลเชิงตัวเลข
120105 แปลได้ว่า ผู้ถูกสำรวจลำดับที่ 12 เป็นเพศชายศึกษาในคณะเทคโนโลยีอุตสาหกรรม
980201 แปลได้ว่า ผู้ถูกสำรวจลำดับที่ 98 เป็นเพศหญิงศึกษาในคณะวิทยาศาสตร์
ซึ่งการเก็บช้อมูลเชิงตัวเลขจะมีประโยชน์สำหรับการดึงข้อมูลผ่านฟังก์ชันทางคณิตศาสตร์เช่นหากเราต้องการดึงข้อมูลผู้ถูกสำรวจคณะวิทยาศาสตร์สามารถทำการ print ด้วยการคำนวณ x mod 100 == 3 เป็นต้น
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา



