กราฟของฟังก์ชัน

           ความสัมพันธ์ของอินพุตและเอาท์พุตสามารถเขียนแทนได้ด้วยคู่อันดับสามารถนำมาเขียนเป็นกราฟในระนาบ 2 มิติได้ โดยให้ x เป็นอินพุตและแกน y เป็นเอาท์พุต ตัวอย่างในตารางที่ 1 เขียนแทนกราฟได้ดังนี้

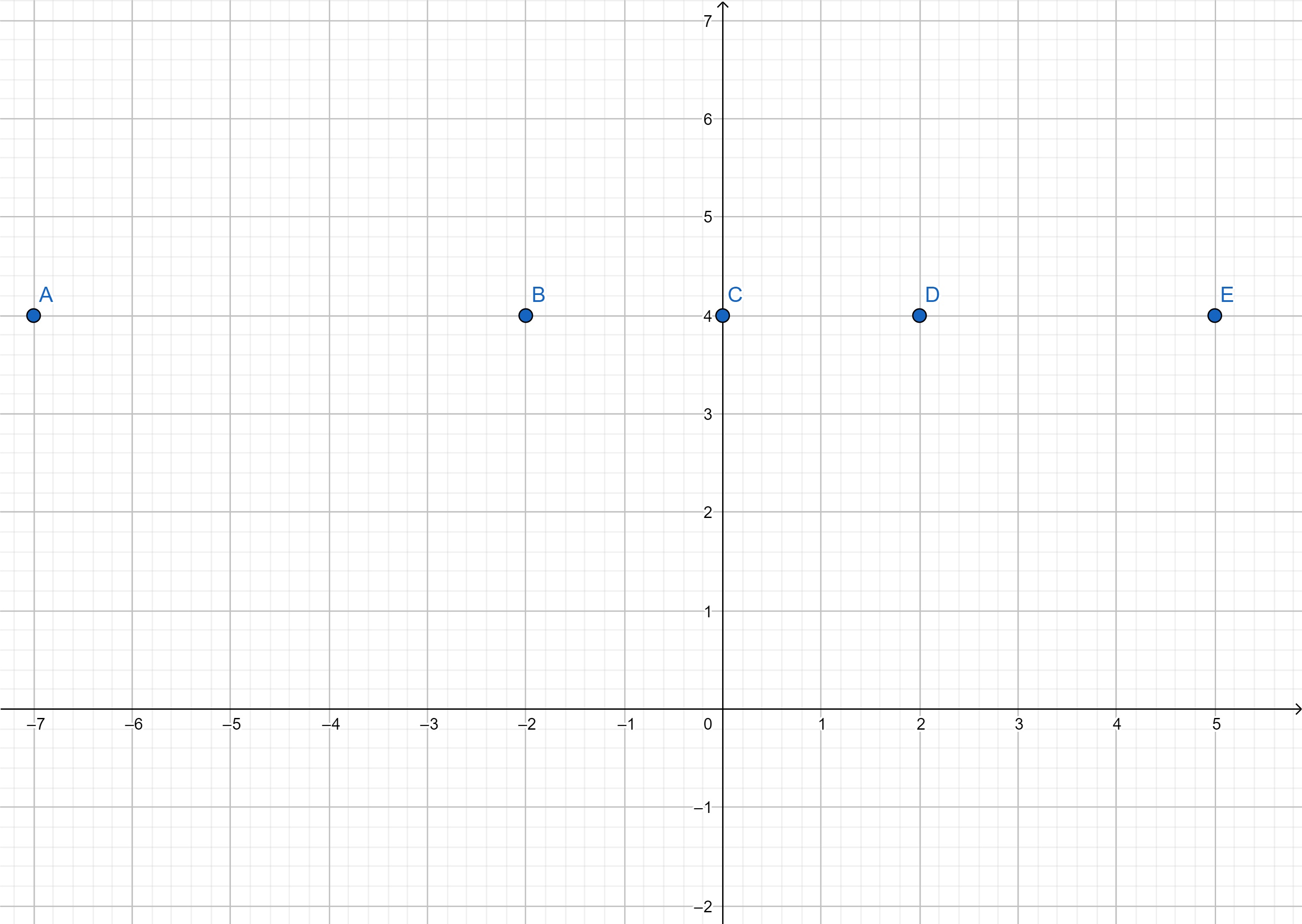
ภาพที่ 2 การสร้างกราฟในตารางที่ 1
เห็นได้ชัดว่ากราฟนี้ลักษณะคงที่ หากเราเขียนภาพตลอดโดนเมนจำนวนจริงของฟังก์ชัน f(x) = 4 จะได้กราฟดังรูป

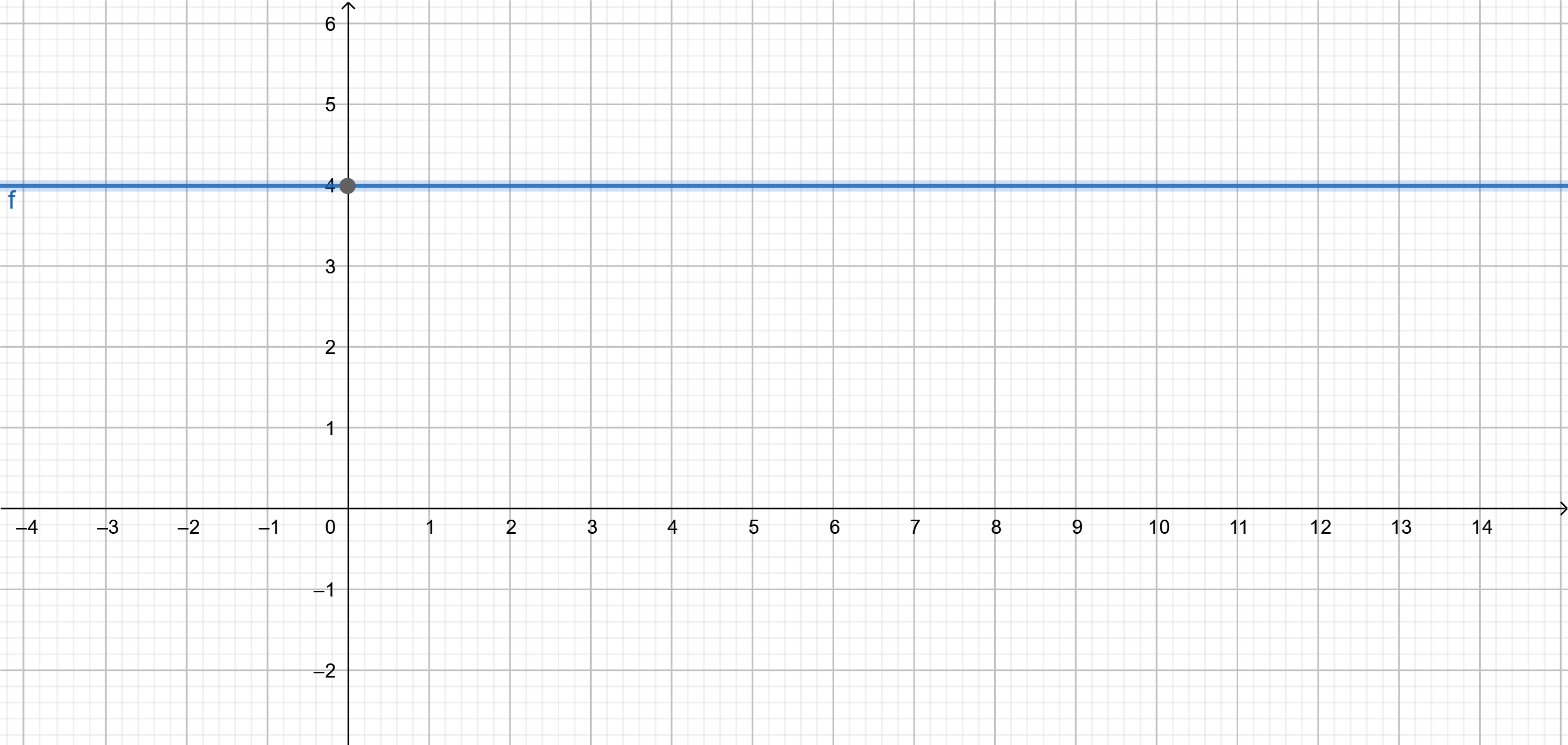
ภาพที่ 3 กราฟ f(x) = 4

สำหรับตารางที่ 2 จะได้กราฟ

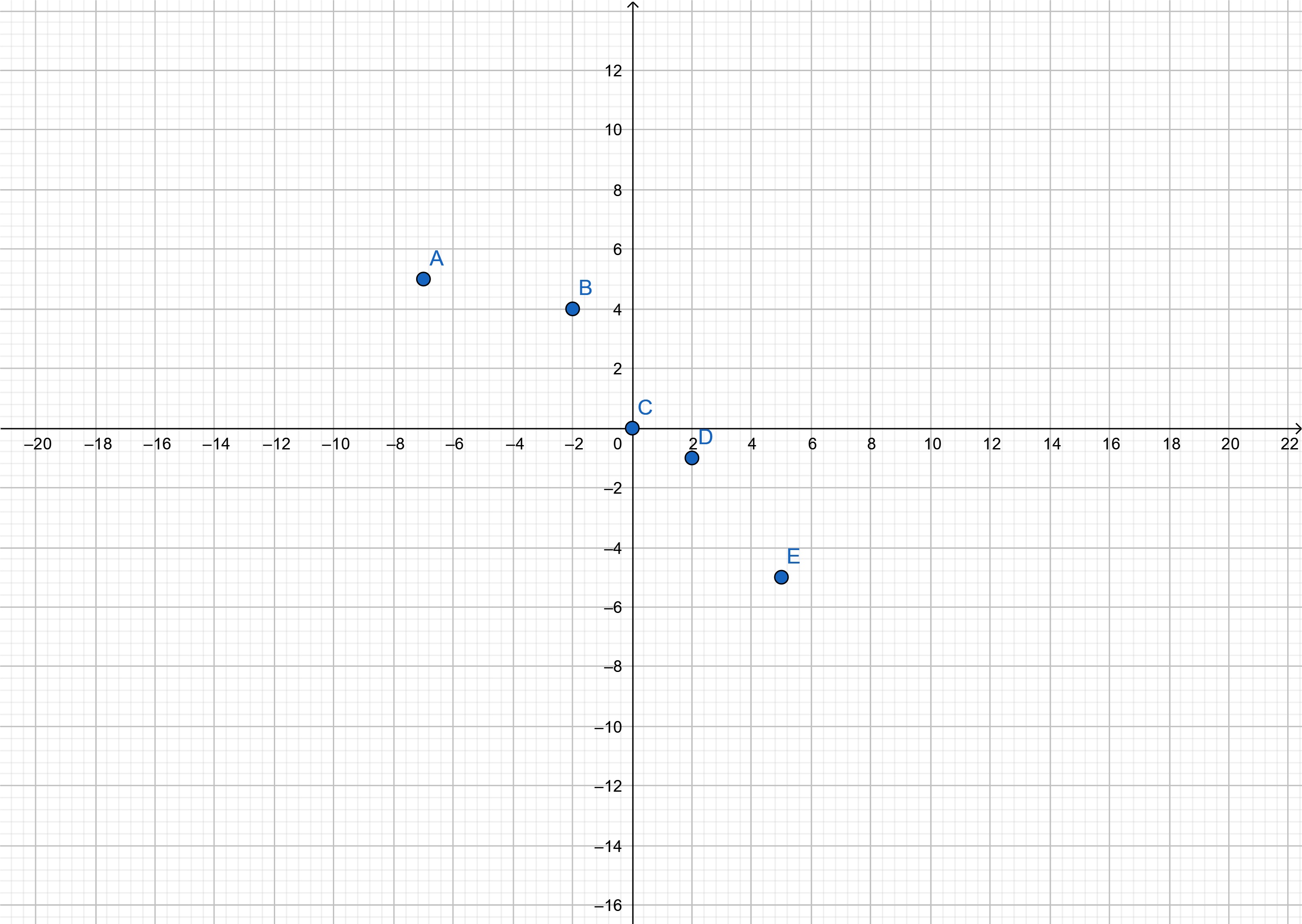
ภาพที่ 4 คู่อันดับ (x,w) ในตารางที่ 2

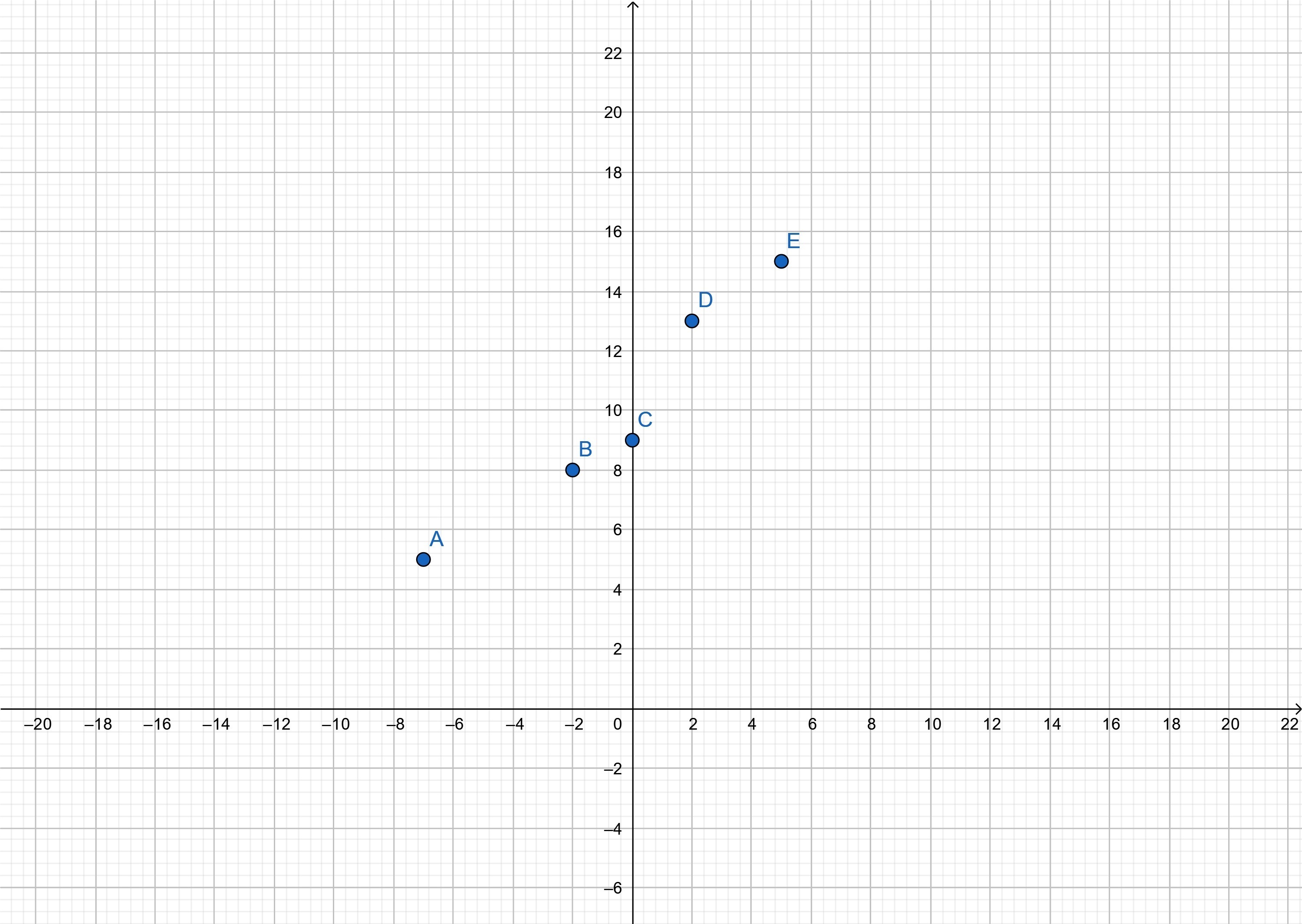
ภาพที่ 5 คู่อันดับ (x,z) ในตารางที่ 2

         จากภาพที่ 4 และภาพที่ 5 พบว่าฟังก์ชันมีแนวโน้มลดและเพิ่มขึ้นตามลำดับ จะเห็นว่าการเขียนกราฟในทำให้เราสามารถมองพฤติกรรมของฟังก์ชันได้ชัดเจนเป็นรูปธรรมมากกว่า

• การเขียนกราฟ

ในทางกลับกันหากเรามีฟังก์ชันที่กำหนดไว้แล้วสามารถนำมาเขียนเป็นกราฟได้ เมื่อนำฟังก์ชันตัวอย่างในตัวอย่างที่ 1 ตัวอย่างที่ 2 และตัวอย่างที่ 3 จะเห็นได้โดยง่ายในภาพที่ 6 จะเห็นว่าแนวโน้มฟังก์ชันเพิ่มเมื่อพิจารณา x ในช่วง [0,5]  และมีแนวโน้มลดลงในช่วง [-5,0]ดังภาพที่ 7 สำหรับภาพที่ 8 จะสังเกตได้ว่าช่วงสำหรับค่า x ในช่วง [-5,5] ไม่สามารถสรุปได้ว่าเพิ่มหรือลดในช่วงดังกล่าว ลักษณะกราฟที่ได้ต่างสอดคล้องกับตัวอย่างในหัวข้อ 1.1

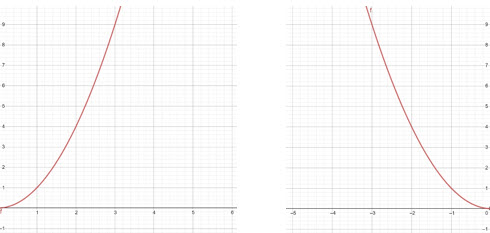
          ภาพที่ 6 กราฟฟังก์ชันตัวอย่างที่ 1                   ภาพที่ 7 กราฟฟังก์ชันตัวอย่างที่ 2

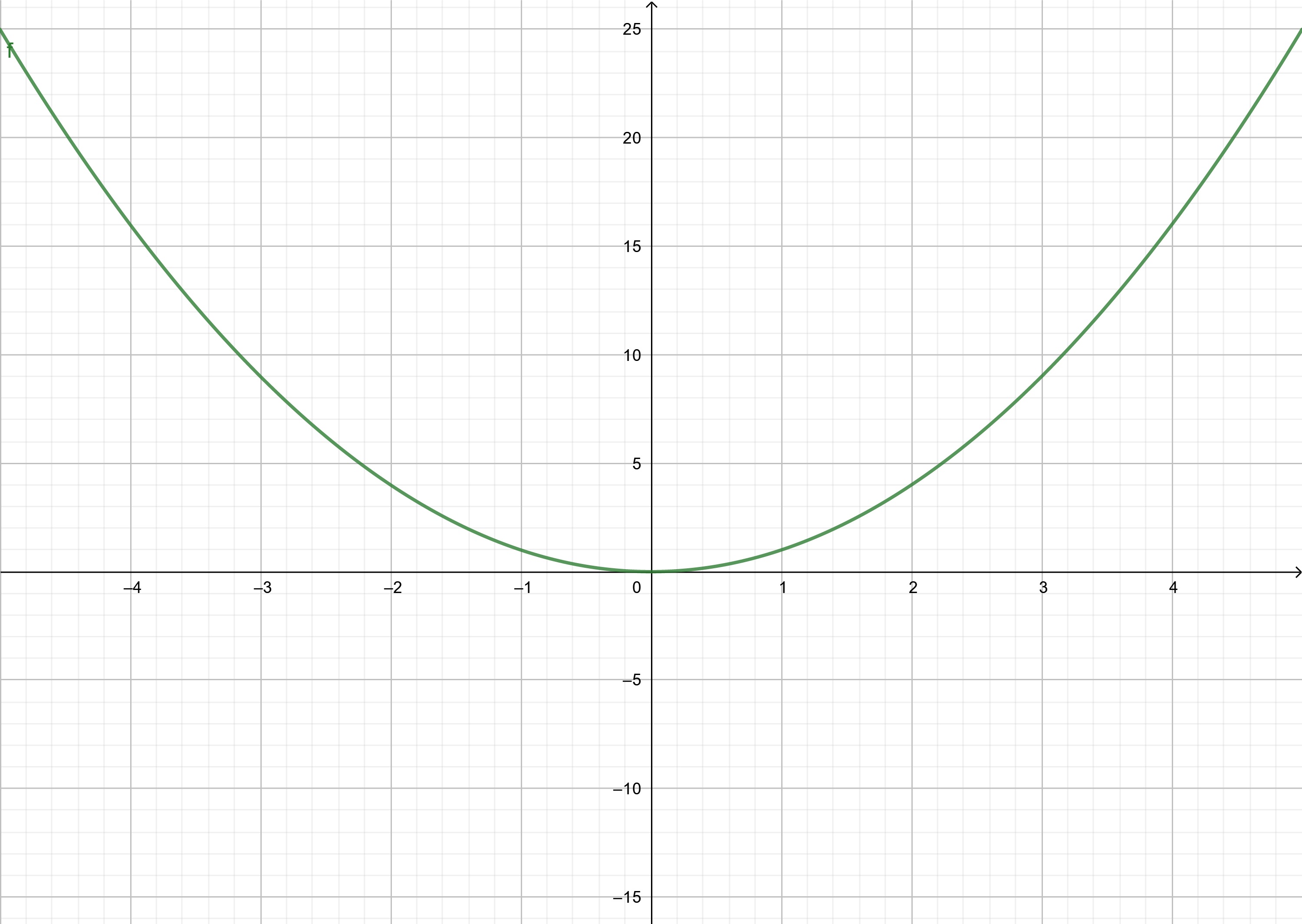
ภาพที่ 8 กราฟฟังก์ชันตัวอย่างที่ 3

          ฟังก์ชันที่มีอินพุตตัวแปรเดียวสามารถแทนได้ด้วยรูปเรขาคณิตในระนาบในส่วนถัดไปเราจะทำศึกษากราฟการดำเนินการบนกราฟและนิพจน์ฟังก์ชันที่เปลี่ยนไป ในหัวข้อ 1.2 ได้ทำการศึกษาการวิเคราะห์ฟังก์ชันสมมาตรเมื่อพิจารณารูปภาพของตารางที่ 2 ดังภาพ 9 และ 10

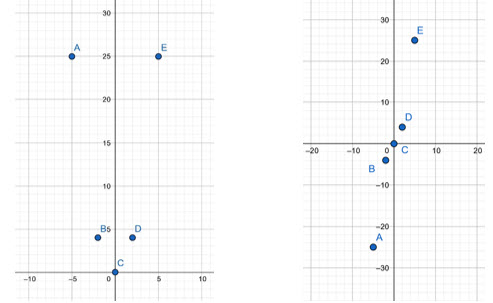
ภาพที่ 9 คู่อันดับ (x,w) ในตารางที่ 3                              ภาพที่ 10 คู่อัน (x,z) ในตารางที่ 3

• การแปลงเรขาคณิตกับกราฟของฟังก์ชัน

          จากภาพที่ 9 พบว่าเป็นเส้นตรง x = 0 ทำหน้าที่เป็นเส้นสะท้อนระหว่างระนาบซ้ายและราบขวา ในขณะที่ภาพที่ 10 เป็นการสะท้อนแบบปฏิสมมาตร ตามที่กล่าวมาเป็นการแปลงเรขาคณิตแบบสะท้อน ก่อนอื่นเราจะศึกษาสมบัติการแปลงที่สำคัญข้อหนึ่งคือการเลื่อนขนาน ในที่นี้ผู้เขียนจะไม่กล่าวถึงสมบัติการหมุนเนื่องจากต้องใช้พีชคณิตเชิงเส้นขั้นสูงในการอธิบาย

          พิจารณากราฟของฟังก์ชัน f(x) = 2x, g(x) = 2(x+2) และ h(x) =2(x-2) ดังภาพที่ 11

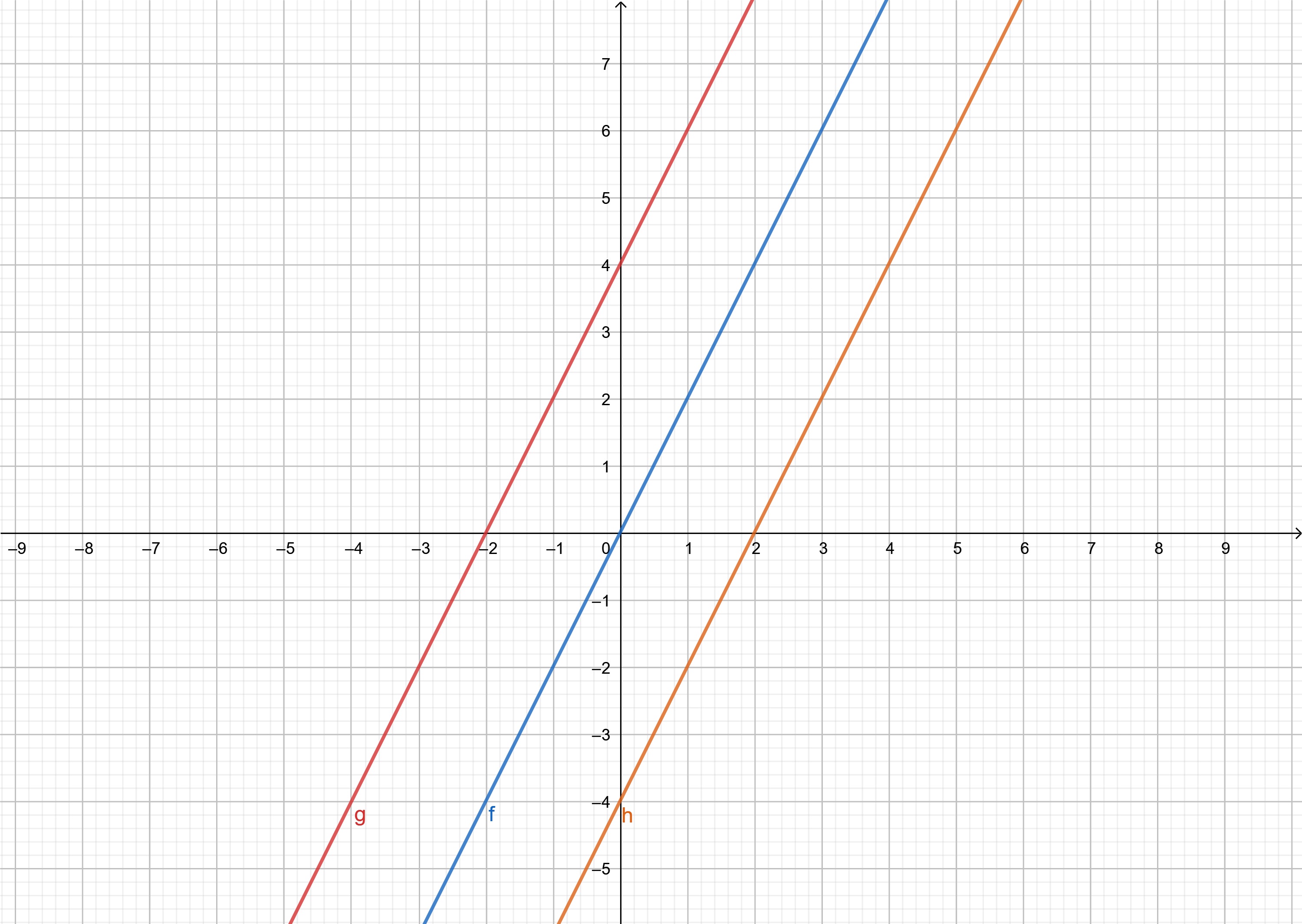
ภาพที่ 11 กราฟฟังก์ชัน f, g   และ h

          จะเห็นว่ากราฟ f, g และ h ขนานกันอธิบายได้ด้วยการเลื่อนขนานทางเรขาคณิตดังนี้

          เขียนฟังก์ชัน g ในรูปของฟังก์ชัน f จะได้ว่า g(x) = 2(x+2) = f(x+2) พบว่ากราฟ g เลื่อนขนานไปในแนวแกน x ทางลบ 2 หน่วย ในทำนองเดียวกันหากเขียน g(x) = 2x + 4 = f(x) + 4 สามารถมองได้อีกแบบหนึ่งว่ากราฟ g คือกราฟ f ที่มีการเลื่อนขนานในแนวแกน y ทางบวก 4 หน่วย สำหรับกราฟ h ถ้าเราเขียน h(x) = f(x-2) กราฟ h คือกราฟ f ที่มีการเลื่อนขนานแกน x ทางบวก 2 หน่วยในขณะที่ h(x) = f(x) – 4 กราฟ h คือกราฟ f ที่มีการเลื่อนขนานแกน y ทางลบจำนวน 4 หน่วยสรุปเป็นหลักการได้ดังนี้

ให้ f เป็นฟังก์ชันใดสมมติให้ h>0 เป็นส่วนเพิ่ม

f(x + h) คือกราฟ f ที่มีการเลื่อนขนานในแนวแกน x ทางลบ h หน่วย

f(x - h) คือกราฟ f ที่มีการเลื่อนขนานในแนวแกน x ทางบวก h หน่วย

f(x) + h คือกราฟ f ที่มีการเลื่อนขนานในแนวแกน y ทางบวก h หน่วย

f(x) – h คือกราฟ f ที่มีการเลื่อนขนานในแนวแกน y ทางลบ h หน่วย

สำหรับคุณสมบัติการสะท้อนนั้นได้ถูกนิยามผ่านฟังก์ชันคู่และฟังก์ชันคี่กล่าวคือ

          ถ้า f(x) = f(-x) กราฟสมมาตรตามแนวแกน x

        ถ้า f(x) = -f(x) กราฟจะปฏิสมมาตรแนวแกน x

ดังภาพที่ 12 และ ภาพที่ 13 ซึ่งเป็นตัวอย่างของฟังก์ชันในตัวอย่างที่ 4 และ 5 ซึ่งเป็นฟังชันก์คู่และฟังก์ชันคี่มีลักษณะสมมาตรและปฏิสมมาตรตามลำดับ

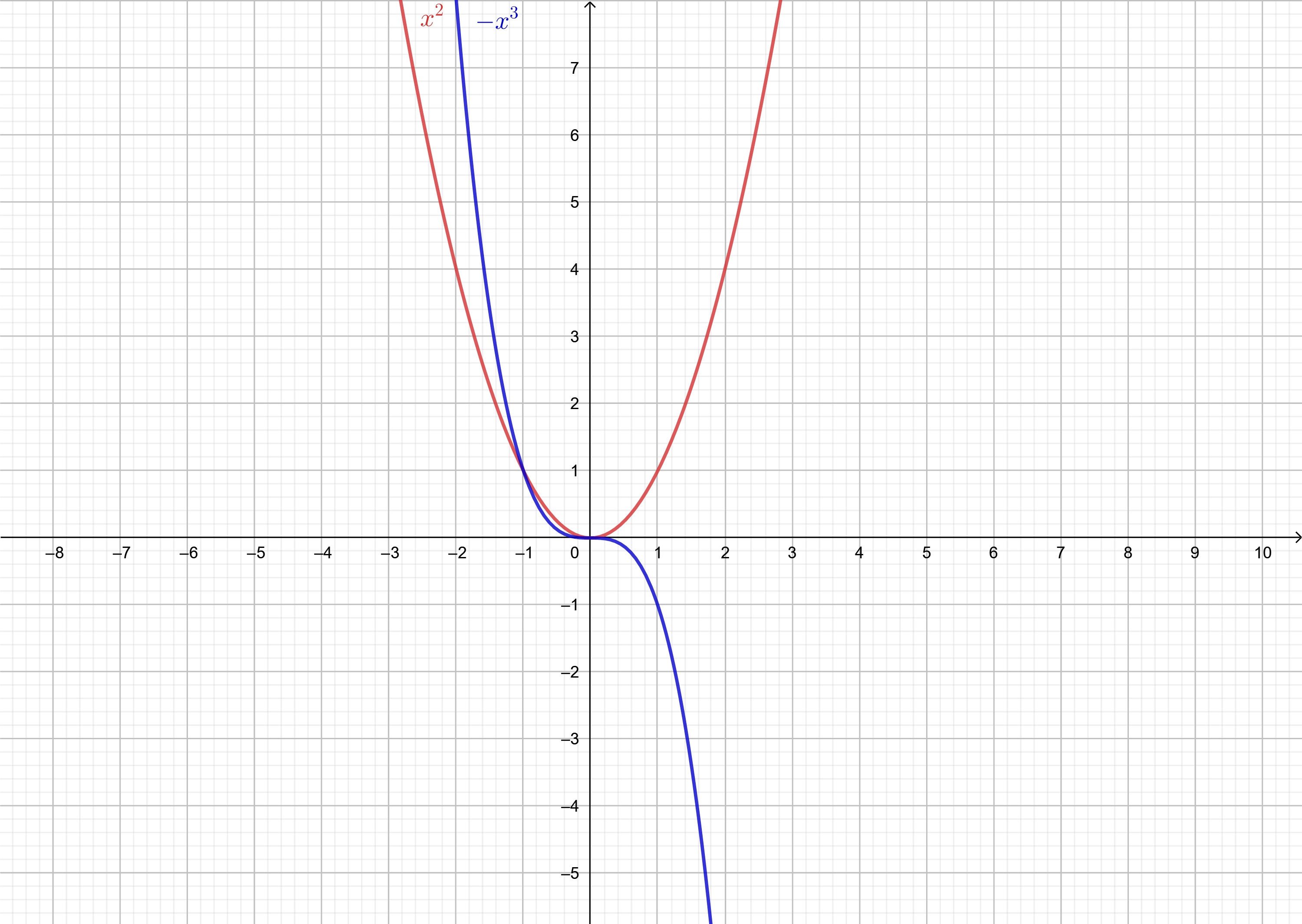
ภาพที่ 12 กราฟสมมาตรกับแกน x (สีแดง) และ กราฟปฏิสมมาตร (สีน้ำเงิน)

ฟังก์ชันเชิงเส้น

           ความสัมพันธ์ของคู่อันดับ (x,y) บนผลคูณคาร์ทีเซียนของจำนวนจริงที่เขียนได้ในรูปของ y = ax + b เป็นความสัมพันธ์เชิงเส้น นิยามเป็นฟังก์ชันได้คือ f(x) = ax + b เป็นฟังก์ชันเชิงเส้นและสามารถอธิบายรูปร่างทางเรขาคณิตได้ด้วยเส้นตรงด้วยเซต L = { (x,y), y = ax + b}

• ฟังก์ชันเชิงเส้น

          การอธิบายการเปลี่ยนแปลงในธรรมชาติอย่างง่ายที่สุดคือการอธิบายด้วยฟังก์ชันเชิงเส้น สมมติให้อินพุตมีการเปลี่ยนแปลงจาก x เป็น x + h โดยที่ h > 0 ส่งผลให้ เอาท์พุตเปลี่ยนจาก f(x) เป็น f(x + h) ถ้าอัตราการเปลี่ยนแปลงนี้มีค่าคงที่แล้วฟังก์ชันนี้เรียกว่าฟังก์ชันเชิงเส้น

          [ f(x+h) – f(x)] / [x + h - x] = [f(x+h) – f(x)] / h= m

         จะได้ว่า f(x+h) = f(x) + mh ถ้าให้ x = 0 จะได้ว่า f(h) = f(0) +mh ซึ่ง f(0) คือจุดตัดแกน y และเรียกว่า m ความชัน นิยามฟังก์ชันเชิงเส้นได้ดังนี้

           เรียก f ว่าเป็นฟังก์ชันเชิงเส้นถ้าสามารถเขียน f ได้ในรูปของ f(x) = mx + b เมื่อ m และ b เป็นจำนวนจริงใด

            พิจารณาค่า m

            กรณีที่ m = 0 จะได้ f(x) = b สรุปได้ว่า f เป็นฟังก์ชันคงที่

            กรณีที่ m > 0 เนื่องจาก h > 0 ดังนั้น [f(x+h) - f(x)] > 0 ทำให้ f(x+h) > f(x) สรุปได้ว่า f เป็นฟังก์ชันเพิ่ม

            กรณีที่ m < 0 เนื่องจาก h > 0 ดังนั้น [f(x+h) - f(x)] < 0 ทำให้ f(x+h) < f(x) สรุปได้ว่า f เป็นฟังก์ชันลด

            สอดคล้องกันกับฟังก์ชัน f(x) = 4 (สีน้ำเงิน), g(x) = 3x -2 (สีเขียว) และ h(x) = -2x + 3 (สีแดง) ซึ่งมีความเป็นศูนย์ มากกว่าศูนย์ และน้อยกว่าศูนย์ตามลำดับ

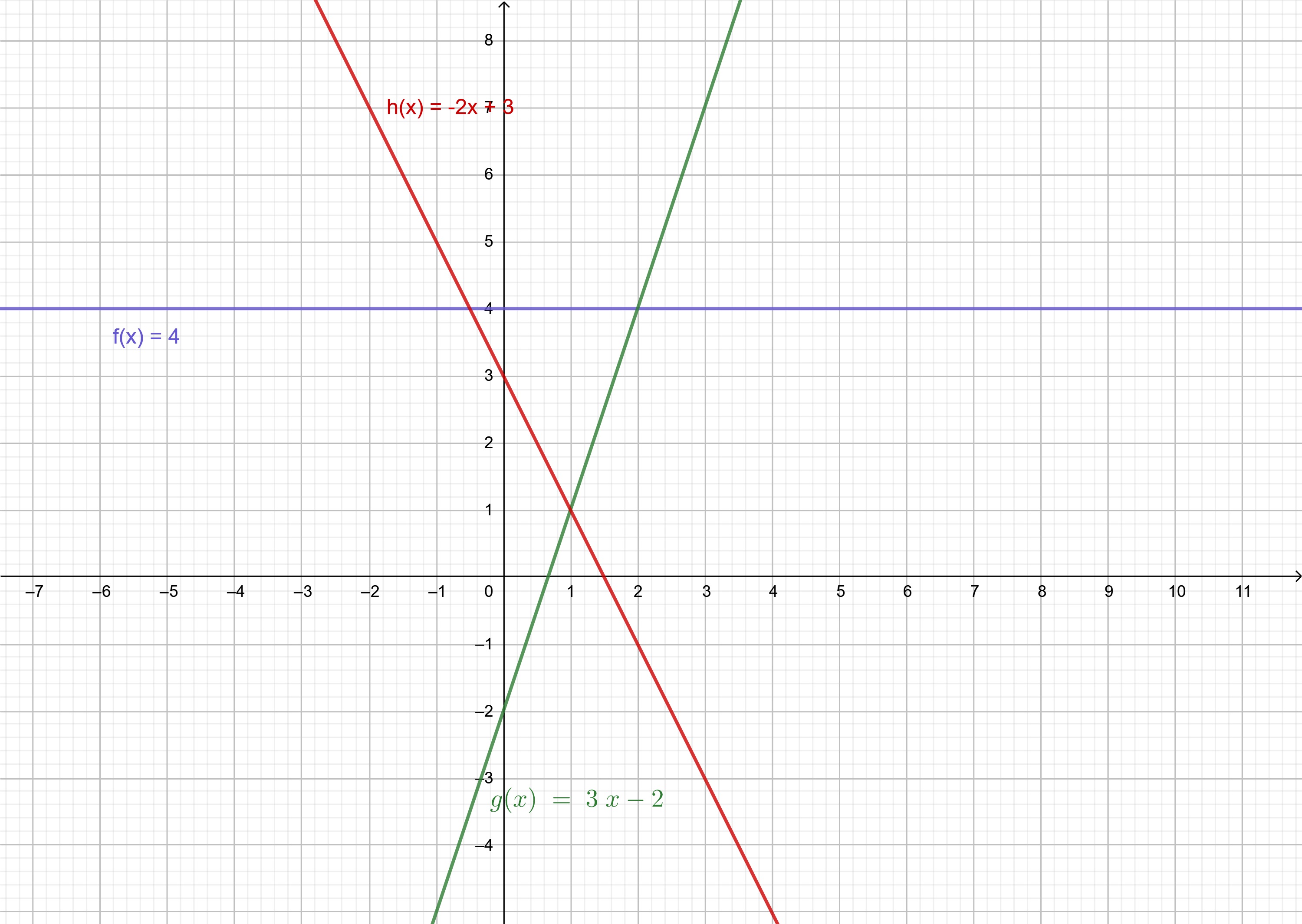
ภาพที่ 13 การแปลผลความชันของเส้นตรงกับพฤติกรรมของฟังก์ชันเชิงเส้น

• พฤติกรรมเชิงเส้น

           ในความเป็นจริงข้อมูลที่ได้มักจะไม่มีลักษณะเป็นเชิงเส้นอย่างชัดเจน อย่างไรก็ตามหากพฤติกรรมมีแนวโน้มเป็นเส้นตรงแล้วเราสามารถประมาณหรือทำนายพฤติกรรมได้ด้วยสมการเชิงเส้น สมมติให้ข้อมูลที่เก็บได้มีจำนวน n ข้อมูลซึ่งเซตของข้อมูลกำหนดโดย { (x1,y1), (x2,y2), … , (xn,yn) } เมื่อนำไปวางจุดแล้วพบว่ามีแนวโน้มเป็นเส้นตรงดังนั้นเราจะหาฟังก์ชันเชิงเส้นในรูป f(x) = ax + b เพื่ออธิบายพฤติกรรมนี้ดังนั้น เอาท์พุต y1 จะถูกประมาณด้วย a(x1) + b โดยมีความคลาดเคลื่อน e1 = y1 – [ a(x1) + b] ซึ่งมีความคลาดเคลื่อนทั้งสิ้น n ค่า ( e1, e2, …, en ) แต่การคำนวณความคลาดเคลื่อนหาก e1 = 1 และ e2 = -1 เมื่อรวมกันแล้วจะได้ e1 + e2 = 0 ตีความได้ว่าไม่มีความคลาดเคลื่อนไม่สมเหตุสมผล ดังนั้นเราจะต้องทำให้เป็นบวกเสมอด้วยการยกกำลังสองจะได้  ei² = (yi – [a(xi) + b])² ด้วยเทคนิคการหาค่าต่ำสุดเราจะได้ระบบสมการ **หมายเหตุสัญลักษณ์ Sigma ในที่นี้หมายถึงผลบวกพจน์ที่ 1 ถึงพจน์ที่ n

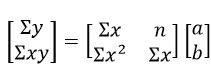
              โดยกฎของเครเมอร์จะได้

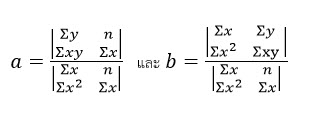
            โดยที่

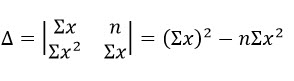
             ในกรณีที่มีการเก็บช้อมูลในรูปของเวกเตอร์ n tuple สมมติให้

              X = (x1,x2,x3,…,xn) และ Y = (y1,y2,y3,…,yn) เราสามารถหาค่าเฉลี่ยของ X และ Y  ขณะเดียวกันพิจารณา

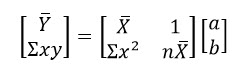
              โดยกฎของเครเมอร์จะได้

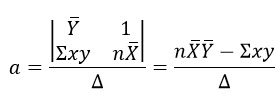
              โดยที่

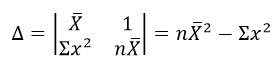
พิจารณา covariance

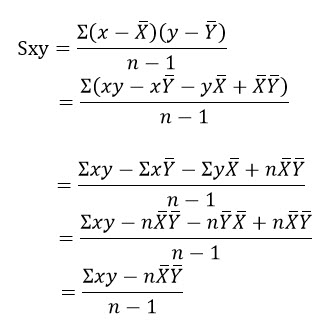
                ในทำนองเดียวกันจะได้

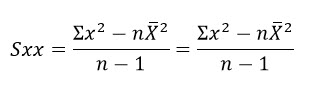
                จึงได้ว่า

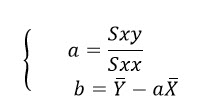
ตัวอย่างที่ 6 ผลการเก็บค่าที่วัดได้จากระบบแสดงดังตาราง

ทำการวิเคราะห์พารามิเตอร์จะได้ว่า

ค่าเฉลี่ย input = 5.7714  , ค่าเฉลี่ย output = 31.5857, Sxx = 62.6743 และ Sxy = 369.0671 ซึ่งแทนสูตรข้างต้นจะได้ a = 5.89 และ b = -2.41 เราจะได้สมการที่ใช้ประมาณคือ y = 5.89 – 2.41

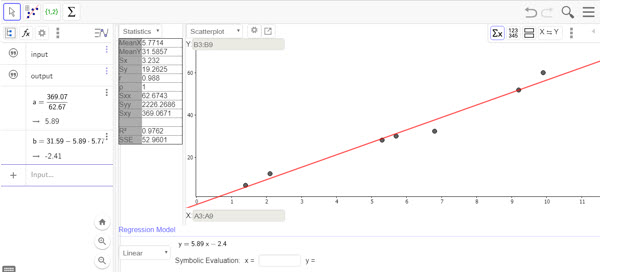
ภาพที่ 14 การประมาณเชิงเส้นด้วยโปรแกรม Geogebra

 ฟังก์ชันกำลังสอง

           ฟังก์ชันพีชคณิตที่มีตัวแปรต้นกำลังศูนย์หรือหนึ่งนั้นเป็นฟังก์ชันเชิงเส้น นอกเหนือจากนี้จะให้กราฟที่มีลักษณะเป็นเส้นโค้งในที่นี้เราจะศึกษาฟังก์ชันที่อยู่ในรูปของพหุนามกำลังสอง

4.1 กราฟฟังก์ชันกำลังสอง

         พหุนามกำลังสองอยู่ในรูปของ ax² + bx + c เมื่อ a, b และ c เป็นจำนวนจริงใด ๆ เรานิยามเป็นฟังก์ชัน

 P(x) = ax² + bx + c

        = a[(x + b/(2a))² -  b²/(4a²) + c/a]

       = a[(x + b/(2a))²  - (b² - 4ac)/(4a²)]

ถ้ากำหนดให้  h = - b/2a และ k = - (b² - 4ac)/(4a) ฟังก์ชันที่อยู่รูป

P(x) = a(x - h)² + k

มีกราฟเป็นรูปพาราโบลา

กรณีที่ a > 0 จะเป็นกราฟพาราโบลาหงายและมีต่ำสุดอยู่ที่จุด (h,k)

กรณีที่ a < 0 จะเป็นกราฟพาราโบลาคว่ำมีจุดสูงสุดอยู่ที่จุด (h,k)

ตัวอย่างที่ 7 ให้ f(x) = 3x² + 18x + 28 จะได้ว่า a =3, b= 18 และ c = 28 พิจารณา h = - b/2a = -3 และ k = - (b² - 4ac)/(4a)  = - (18² – 4x3x28)/(4x3²) = 1 นั้นคือ f(x) = 3(x + 3)² + 1 เนื่องจาก a > 0 กราฟเป็นรูปพาราโบลาหงายมีจุดยอดเป็นจุดต่ำสุดที่ (-3,1) ดังภาพที่ 15

ตัวอย่างที่ 8 ให้ f(x) = -3x² + 18x + 28 จะได้ว่า a =-3, b= 18 และ c = 28 พิจารณา h = - b/2a = 3 และ k = - (b² - 4ac)/(4a)  = 7 นั้นคือ f(x) = 3(x - 3)² + 7 เนื่องจาก a < 0 กราฟเป็นรูปพาราโบลาคว่ำมีจุดยอดเป็นจุดสูงสุดที่ (3,7) ดังภาพที่ 16

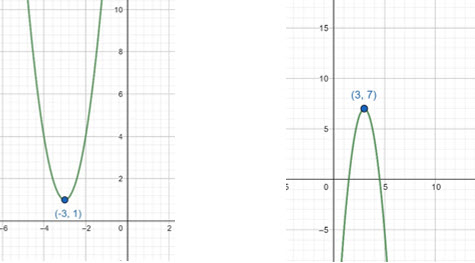
ภาพที่ 15  กราฟพาราโบลาของตัวอย่างที่ 7     ภาพที่ 16  กราฟพาราโบลาของตัวอย่างที่ 8

4.2 ฟังก์ชันกำลังกับคำตอบของสมการพหุนามกำลังสอง

          ที่กล่าวมาข้างต้นเป็นการศึกษาฟังก์ชันกำลังสองบนแนวคิดของภาคตัดกรวยที่มีรูปร่างเป็นพาราโบลาต่อไปเราจะศึกษาฟังก์ชันกำลังสองบนแนวคิดของพีชคณิต ย้อนกลับไปที่สมการพหุนามกำลัง 2 ในระบบจำนวนจริงจะพบว่าสมการที่อยู่ในรูป ax² + bx + c = 0 จะมีคำตอบได้สามกรณีขึ้นค่า discriminant D = b² – 4ac

กรณีที่ D < 0 สมการไม่มีคำตอบที่เป็นจำนวนจริง

กรณีที่ D = 0 สมการมีคำตอบเพียงคำตอบเดียว

กรณีที่ D > 0 สมการมีคำตอบเป็นจำนวนจริง 2 คำตอบ

          จากสมการดังกล่าว ถ้าให้ f(x) = ax² + bx + c และให้ r เป็นคำตอบของสมการแล้ว เมื่อนำไปแทนค่าในสมการจะได้ ar² + br + c = 0 สรุปได้ว่า ถ้า r เป็นคำตอบของสมการพหุนามกำลังสองแล้ว f(r) = 0 เขียนได้ในรูปคู่อันดับ (r,0) ที่ซึ่งเป็นจุดบนแกน x พิจารณาตัวอย่างของสมการพหุนามต่อไปนี้ต่อไปนี้

ตัวอย่างที่ 9 พิจารสมการ 6x² + 23x - 18 = 0

          พิจารณา D = 23² – 4x6x(-18) > 0 สมการนี้มีคำตอบเป็นจำนวนจริงสองคำตอบ หาจำนวนสองจำนวนที่ซึ่งผลคูณเท่ากับ 6x(-18) = - 108 แต่มีผลบวกเท่ากับ 23 จะได้ว่าจำนวนสองจำนวนนั้นคือ 27 และ – 4 ดังนั้น 6x² + 23x – 18 = 6x² – 4x + 27x – 18 = 2x(3x – 2) + 9(3x – 2) = (3x – 2)(2x + 9) = 0 ดังนั้นคำตอบสมการคือ {2/3, -9/2} เมื่อพิจารณากราฟคำตอบจะพบว่าเส้นกราฟตัดแกน x ที่จุด (2/3,0) และ (-9/2,0) ดังภาพที่ 17

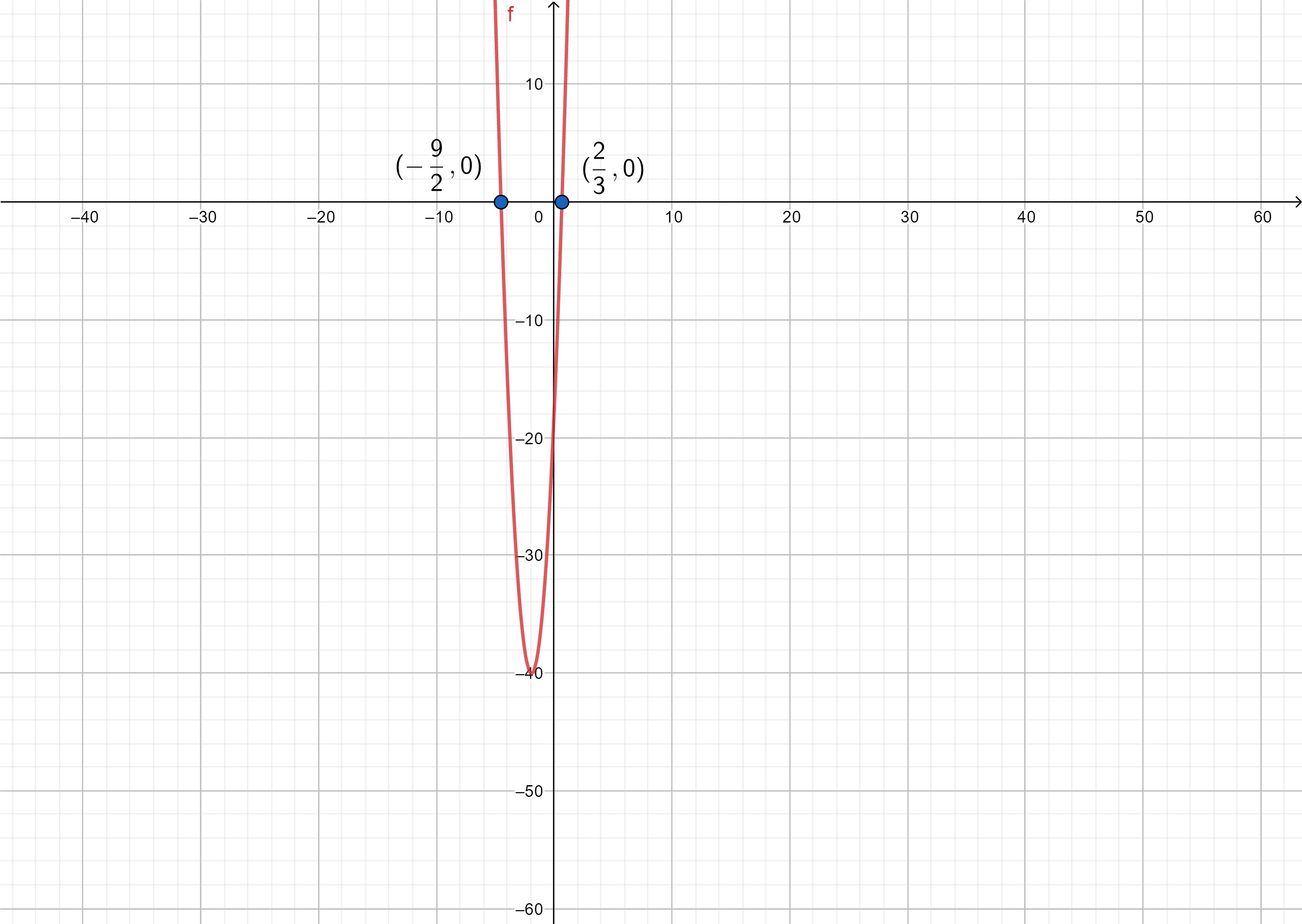
ภาพที่ 17 กราฟของฟังก์ชัน f(x) = 6x² + 23x - 18

ตัวอย่างที่ 10 พิจารณาสมการ 4x² + 20x +25 = 0

พิจารณา D = 20² – 4x4x25 = 0 สมการนี้มีคำตอบเป็นจำนวนจริงเพียงคำตอบเดียวดังนั้น

4x² + 20x + 25 = (2x)² + 2(2x)(5) + 5² = (2x+5)² = 0

ดังนั้นคำตอบสมการคือ {-5/2} เมื่อพิจารณากราฟคำตอบจะพบว่าเส้นกราฟตัดแกน x ที่จุด (-5/2,0) เพียงจุดเดียวดังภาพที่ 18

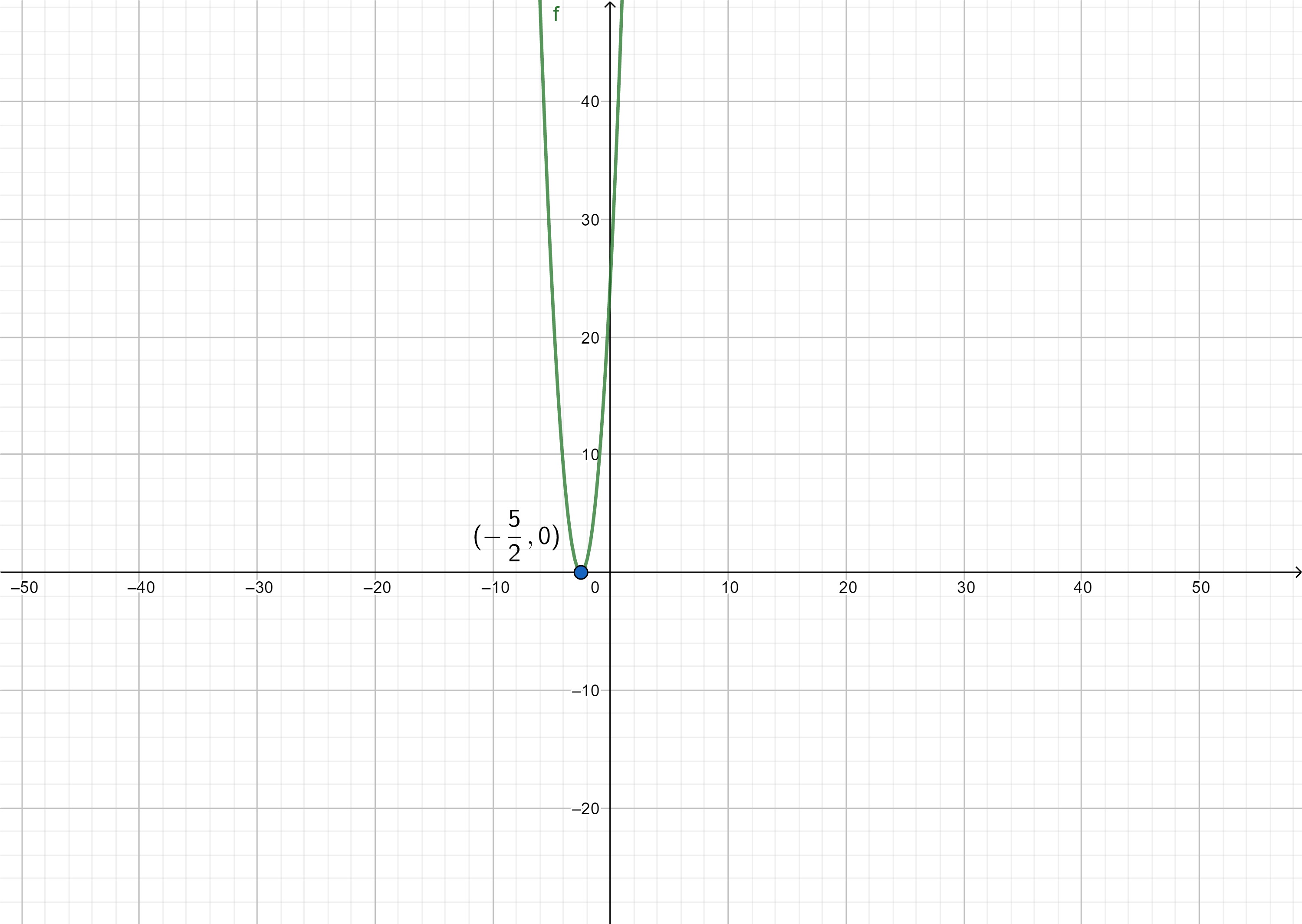
ภาพที่ 18 กราฟของฟังก์ชัน f(x) = 4x² + 20x + 15

ตัวอย่างที่ 11 พิจารณาสมการ 2x² + 2x + 5 = 0

พิจารณา D = 2² – 4x2x5 < 0 สมการนี้ไม่มีคำตอบที่เป็นจำนวนจริง เนื่องจาก

2x² + 2x + 5 = 2(x² + x) + 5 = 2(x + 0.5)² - 0.25 + 5 = 2(x + 0.5)² + 4.75 >= 4.75

พหุนามมีค่ามากกว่าหรือเท่ากับ 4.75 เสมอ ดังนั้นไม่มีจำนวนจริง x ที่ทำให้ 2x² + 2x + 5 = 0 ในภาพที่ 19 เส้นกราฟของฟังก์ชันจึงไม่ตัดแกน x

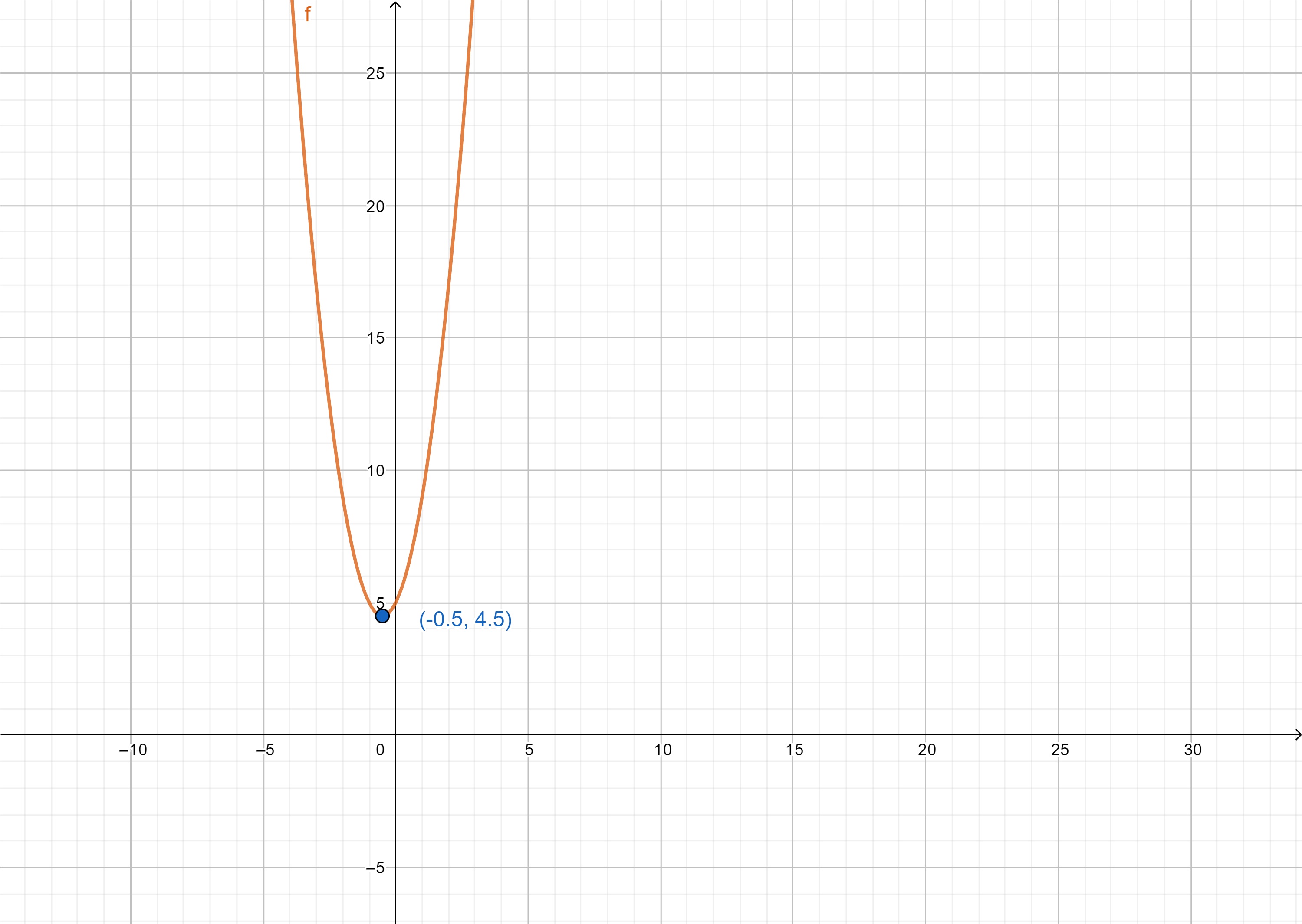
ภาพที่ 19 กราฟของฟังก์ชัน f(x) = 2x² + 2x + 5

 ฟังก์ชันพหุนาม

          ให้ P(x) ฟังก์ชันพหุนามดีกรี n เขียนได้ในรูป

          P(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ

          เรียก a_i สำหรับ i = 1,2,3,…, n ว่าสัมประสิทธิ์ กรณีที่สัมประสิทธิ์นำ a_n = 1 เรียกพหุนามนี้ว่าพหุนามโมนิค ในหัวข้อนี้เราจะศึกษาเกี่ยวกับพหุนามโมนิค จากทฤษฎีมูลฐานของพีชคณิตเราจะพบว่า พหุนามดีกรี n นั้นจะประกอบด้วยรากจำนวน n รากในที่นี้แทนด้วย k1, k2, …, kn นั้นคือ

          P(x) = (x – k1)(x – k2)…(x – kn)

          ในกรณีที่รากเป็นจำนวนจริงเราจะได้ว่ากราฟพหุนามจะตัดแกน x จำนวน n ครั้งในกรณีที่ k1, k2,…, kn แตกต่างกันทั้งหมด แต่ในกรณีที่มีรากซ้ำเส้นกราฟจะตัดแกน x ที่ค่ารากเพียงครั้งเดียวซึ่งผู้เขียนจะยกตัวอย่างพหุนามกำลังสามประกอบตัวเพื่อความสะดวกจะพิจารณาพหุนามโมนิคที่มีค่ารากเป็นจำนวนเต็มซึ่งในกรณีที่รากเป็นจำนวนจำนวนจริงใด ๆ แนวคิดในการวิเคราะห์เป็นไปในทำนองเดียวกัน สมมติให้มีราก 3 รากประกอบด้วย k1, k2 และ k3 เราจะวิเคราะห์ประเภทกราฟจากการซ้ำของรากพหุนาม 3 กรณีคือ กรณีไม่มีรากซ้ำ {k1, k2, k3} , กรณีมีรากซ้ำ 1 ค่า { 2(k1), k2} , กรณีที่มีรากซ้ำกัน 3 ค่า {3(k1)}

ตัวอย่างที่ 12  พิจารณากราฟพหุนาม P(x) = (x-1)(x+2)(x+5) ในภาพที่ 20 จะพบว่าพหุนามมีรากแตกต่างกัน 3 ค่าคือ { -5, -2, 1 } กราฟฟังก์ชันจึงตัดแกน x ที่จุด (-5,0), (-2,0) และ (1,0)

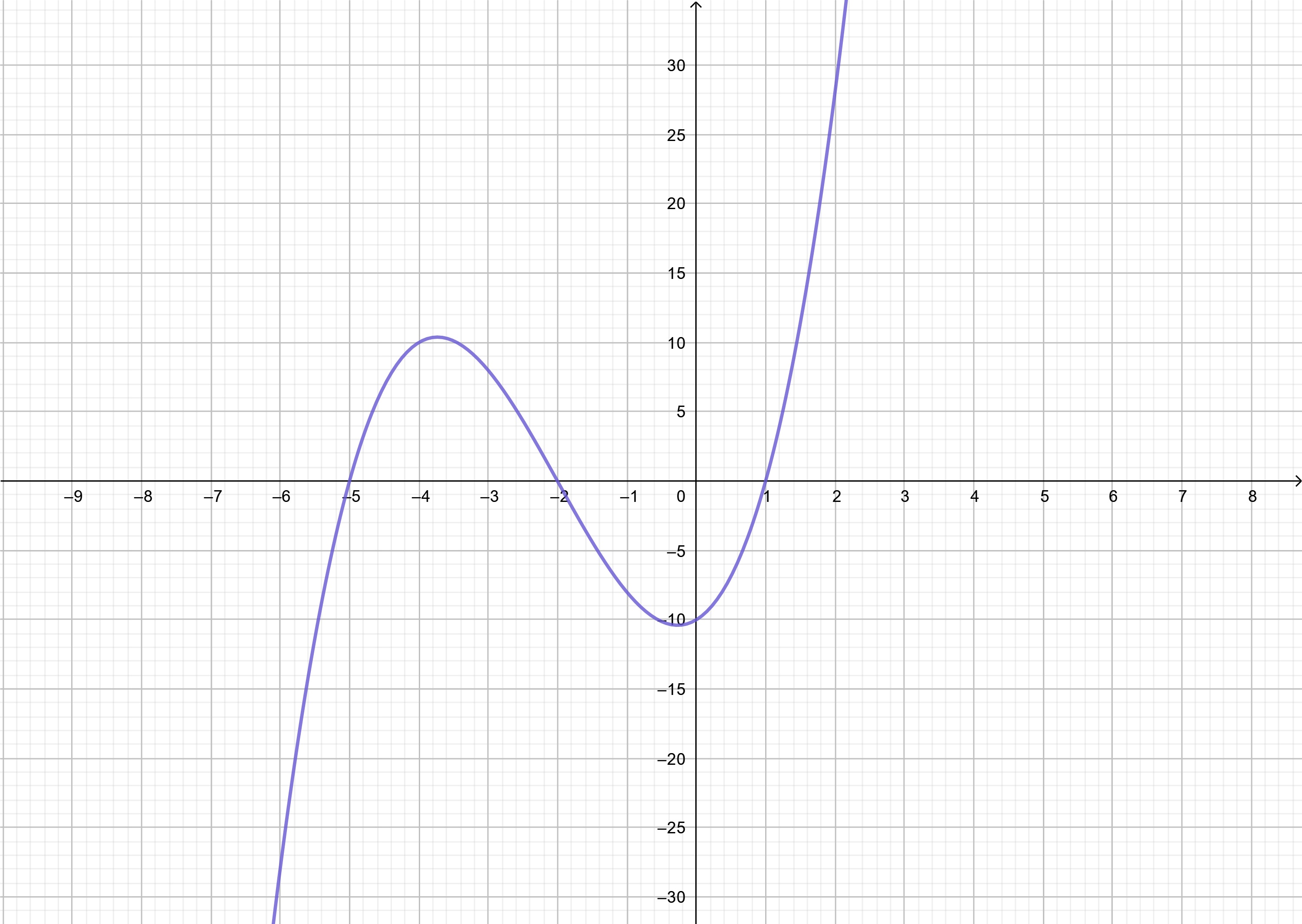
ภาพที่ 20 กราฟฟังก์ชัน P(x) = (x-1)(x+2)(x+5)

          หากเราทำการวิเคราะห์ค่าของฟังก์ชันตามโดเมนของฟังก์ชันจะพบว่าโดเมนถูกแบ่งออกเป็น 4 ส่วนคือ

          P1 = (-infinity,-5), P2 = (-5,-2), P3 = (-2,1), P4 = (1,infinity) พบว่า

          ค่า x ที่อยู่ในช่วงของ P1 จะทำให้ค่าฟังก์ชันเป็นลบ

          ค่า x ที่อยู่ในช่วงของ P2 จะทำให้ค่าฟังก์ชันเป็นบวก

          ค่า x ที่อยู่ในช่วงของ P3 จะทำให้ค่าฟังก์ชันเป็นลบ

          ค่า x ที่อยู่ในช่วงของ P4 จะทำให้ค่าฟังก์ชันเป็นบวก

          จากการสังเกตตำแหน่งค่าราก x = -5, x = -2 และ x = 1 พบว่าค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายที่แตกต่างกัน

ตัวอย่างที่ 13 พิจารณากราฟพหุนาม P(x) = (x-1)(x-1)(x+2) ในภาพที่ 21 พบว่าพหุนามมีรากแตกต่างกัน 2 ค่าและมีรากซ้ำ 1 ค่าคือ { -2, 2(1) } กราฟฟังก์ชันจึงตัดแกน x ที่จุด (-2,0) และ (1,0)

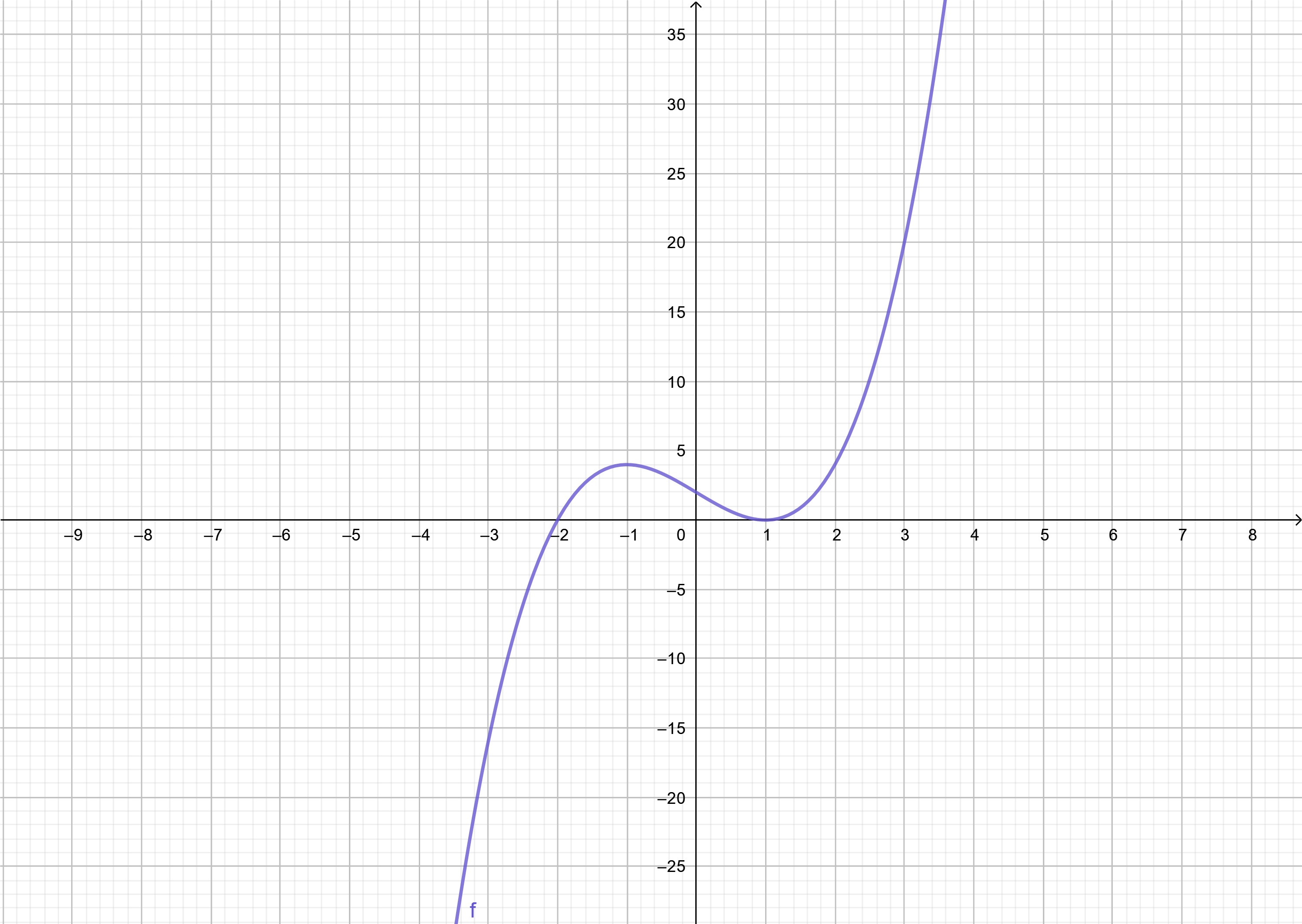
ภาพที่ 21 กราฟฟังก์ชัน P(x) = (x-1)(x-1)(x+2)

          วิเคราะห์ค่าของฟังก์ชันตามโดเมนของฟังก์ชันจะพบว่าโดเมนถูกแบ่งออกเป็น 3 ส่วนคือ

          P1 = (-infinity,-2), P2 = (-2,1), P3 = (1,infinity) พบว่า

          ค่า x ที่อยู่ในช่วงของ P1 จะทำให้ค่าฟังก์ชันเป็นลบ

          ค่า x ที่อยู่ในช่วงของ P2 จะทำให้ค่าฟังก์ชันเป็นบวก

          ค่า x ที่อยู่ในช่วงของ P3 จะทำให้ค่าฟังก์ชันเป็นบวก

          จากการสังเกตตำแหน่งค่าราก x = -2 พบว่าค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายที่แตกต่างกันแต่ ณ ตำแหน่งของ x = 1 ซึ่งเป็นรากซ้ำกลับพบว่าค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายเหมือนกัน

ตัวอย่างที่ 14 พิจารณากราฟพหุนาม P(x) = (x-1)(x-1)(x-1) ในภาพที่ 22 พบว่าพหุนามมีรากซ้ำ 3 ค่าคือ { 3(1) } กราฟฟังก์ชันจึงตัดแกน x เพียงจุดเดียวคือจุด (1,0)

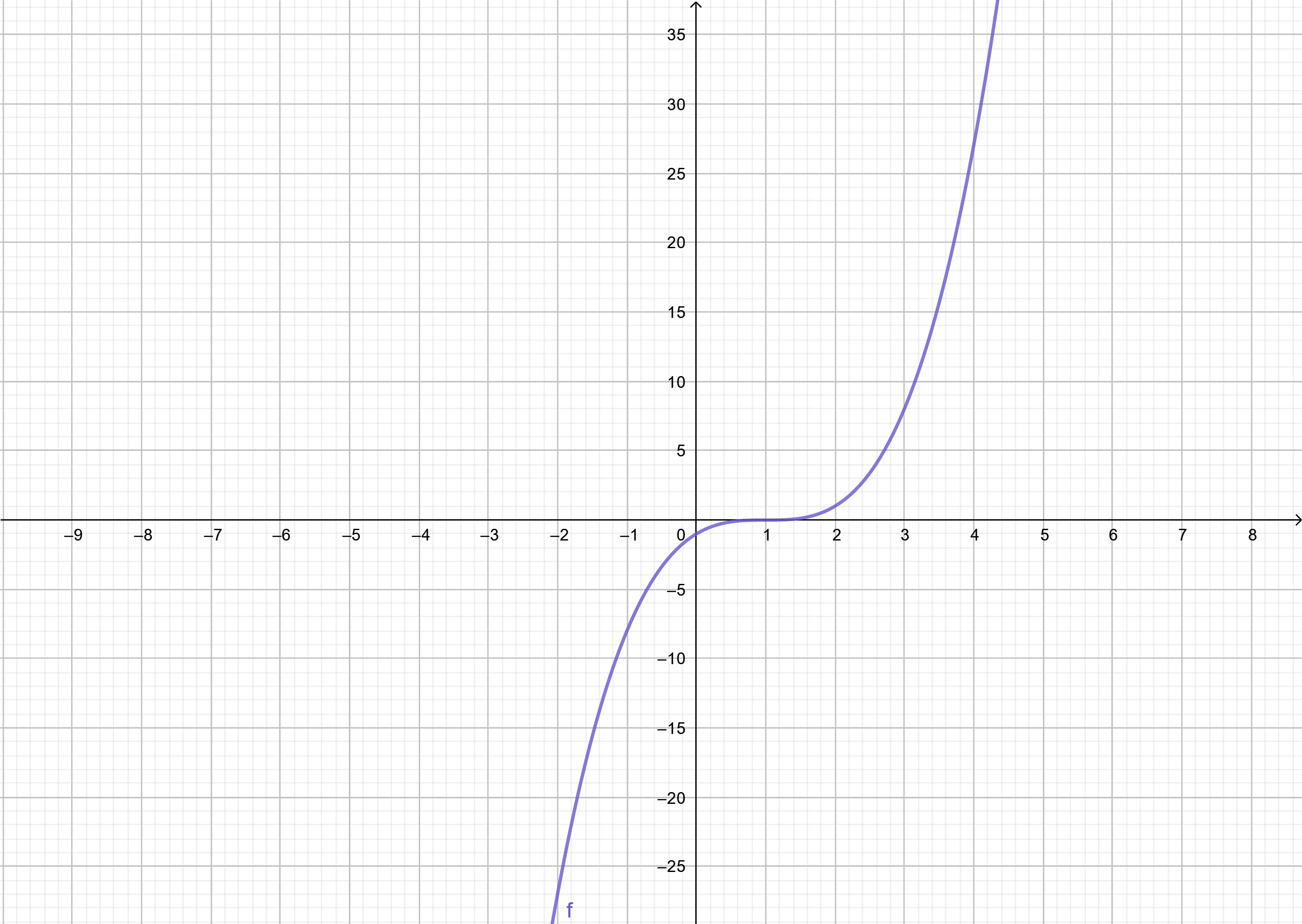
ภาพที่ 22 กราฟฟังก์ชัน P(x) = (x-1)(x-1)(x-1)

          ในกรณีนี้โดเมนของฟังก์ชันถูกแบ่งออกเป็น 2 ส่วนคือ

          P1 = (-infinity,1) และ P2 = (1,infinity) พบว่า

          ค่า x ที่อยู่ในช่วงของ P1 จะทำให้ค่าฟังก์ชันเป็นลบ

          ค่า x ที่อยู่ในช่วงของ P2 จะทำให้ค่าฟังก์ชันเป็นบวก

          พบว่าที่ตำแหน่งค่าราก x = 1 ค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายที่แตกต่างกัน

 ฟังก์ชันเชิงสัดส่วน 

          ฟังก์ชันเชิงสัดส่วนคือฟังก์ชันที่เขียนอยู่ในรูปของเศษส่วน เงื่อนไขสำคัญที่จะต้องพิจารณาเสมอสำหรับการเขียนในรูปเศษส่วนคือตัวเศษจะต้องไปเป็นศูนย์ ในหัวข้อนี้เราจะพิจารณากราฟของฟังก์ชันเชิงสัดส่วนที่มีตัวเศษและตัวส่วนเป็นพหุนาม และจะกล่าวถึงเทคนิคสำคัญสำหรับการแก้ปัญหาฟังก์ชันเชิงสัดส่วนคือการแยกเศษส่วนย่อย

• ฟังก์ชันเชิงสัดส่วน

กำหนดให้ A(x) และ B(x) เป็นพหุนามถ้า Q(x) = A(x) / B(x) โดยที่ B(x) ไม่เท่ากับศูนย์ เราจะทำการวิเคราะห์ฟังก์ชันเชิงสัดส่วนด้วยการเขียนกราฟจากตัวอย่างต่อไปนี้

ตัวอย่างที่ 15 พิจารณากราฟ f(x) = 1 / (x -1 ) จะพบว่าที่ x = 1 ไม่นิยามทำให้ฟังก์ชัน f(1) หาค่าไม่ได้

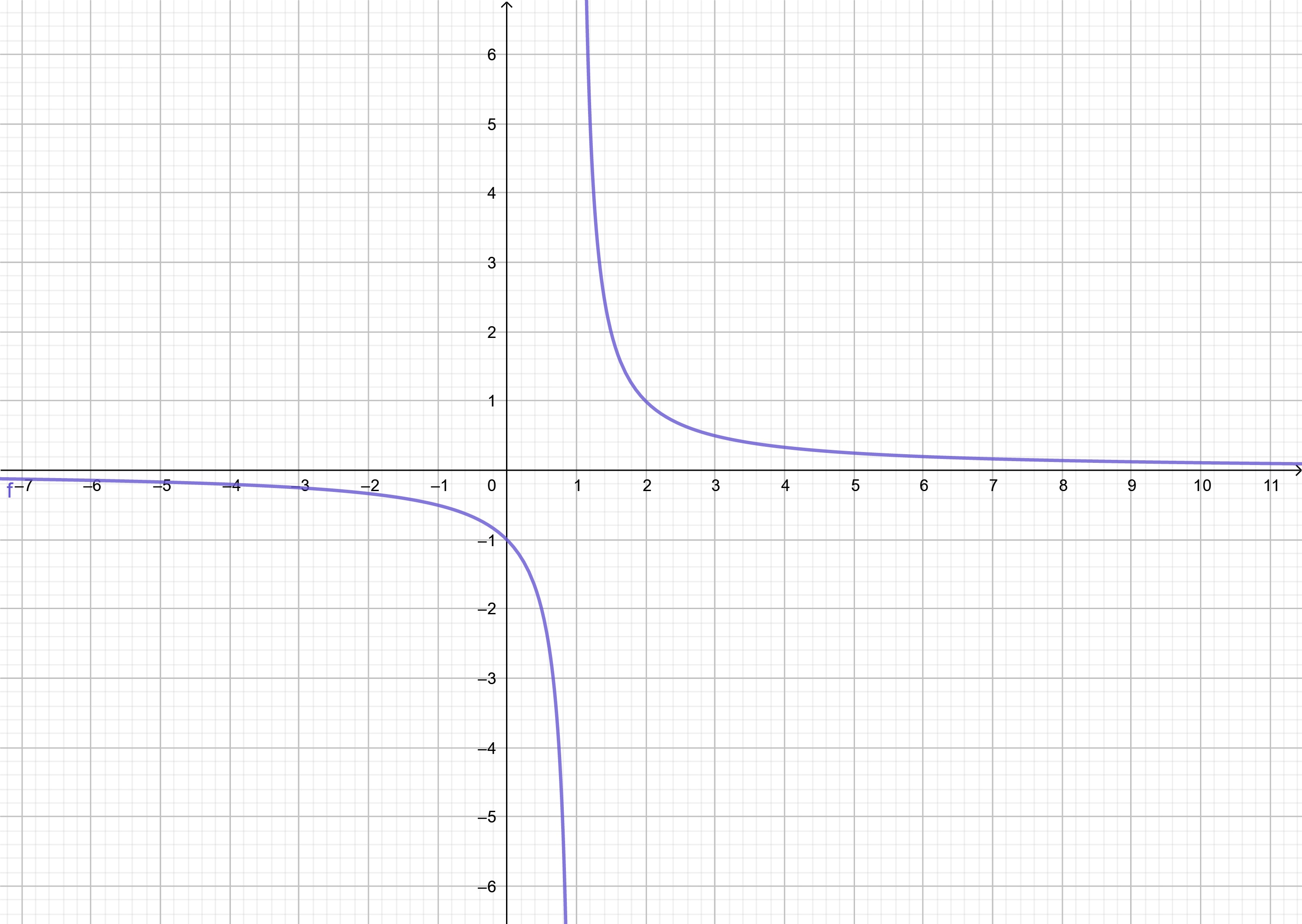
ภาพที่ 23 กราฟฟังก์ชัน 1 / (x -1 )

ตัวอย่างที่ 16 จากกราฟของฟังก์ชัน f(x) = (x² - 1) / (x + 1) จะพบว่า f(-1) ไม่นิยาม แต่สำหรับกรณีที่ x ไม่เท่ากับ 1 เมื่อพิจารณานิพจน์ (x² – 1) / (x + 1) = (x - 1) นั้นคือบริเวณโดเมนที่ไม่ใช่ 1 ฟังก์ชันนี้จะมีพฤติกรรมแบบเดียวกับฟังก์ชัน x - 1

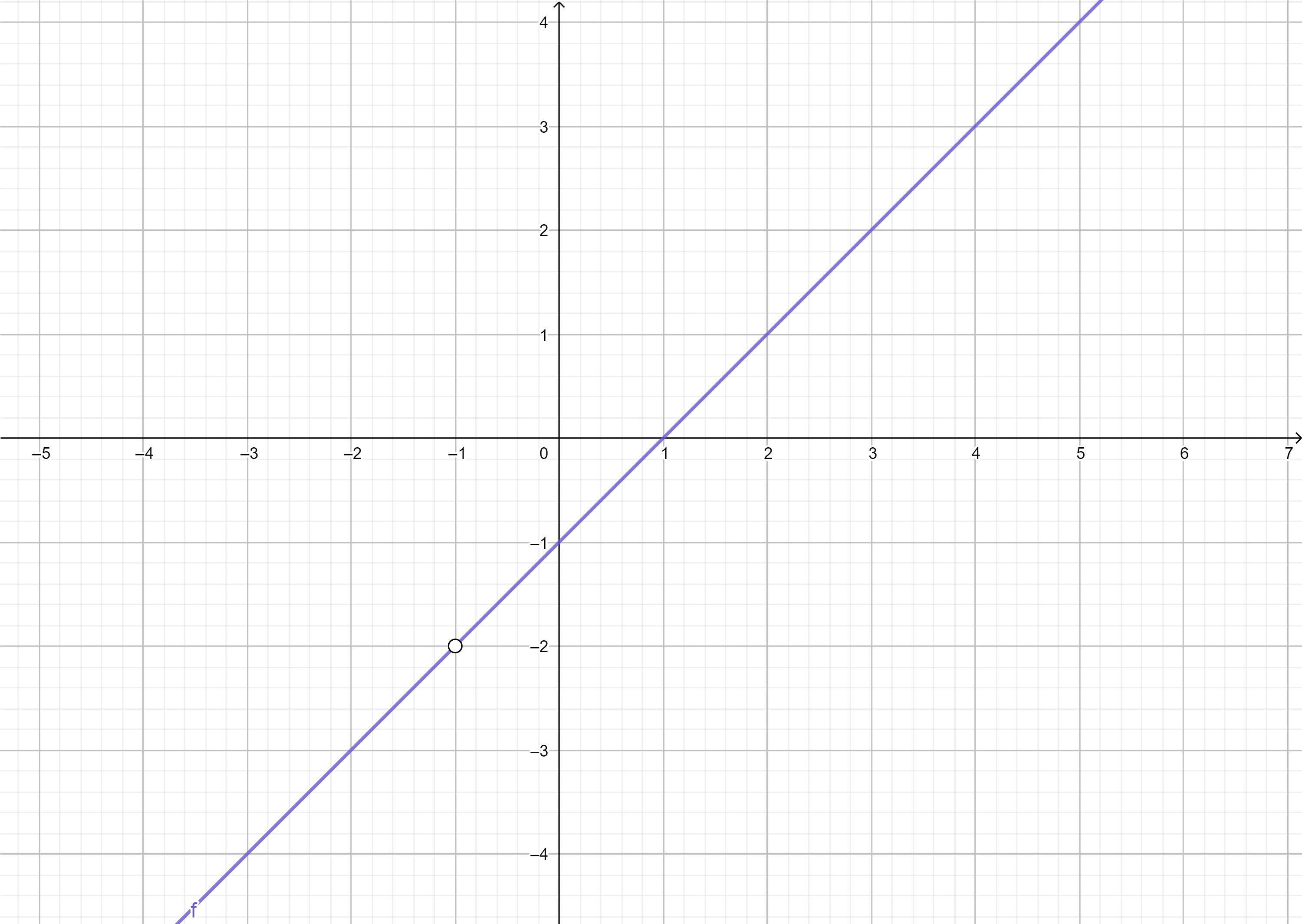
ภาพที่ 23 กราฟฟังก์ชัน (x² - 1) / (x + 1)

ตัวอย่างที่ 17 กราฟของฟังก์ชัน [(x + 1)(x + 2)] / [(x – 2)(x + 3)] ณ จุดที่ไม่นิยามได้แก่ x = 2 และ x = -3 จะพบว่าฟังก์ชันหาค่าไม่ได้และมีแนวโน้มการลู่ออกไปในทิศทางที่ต่างกัน

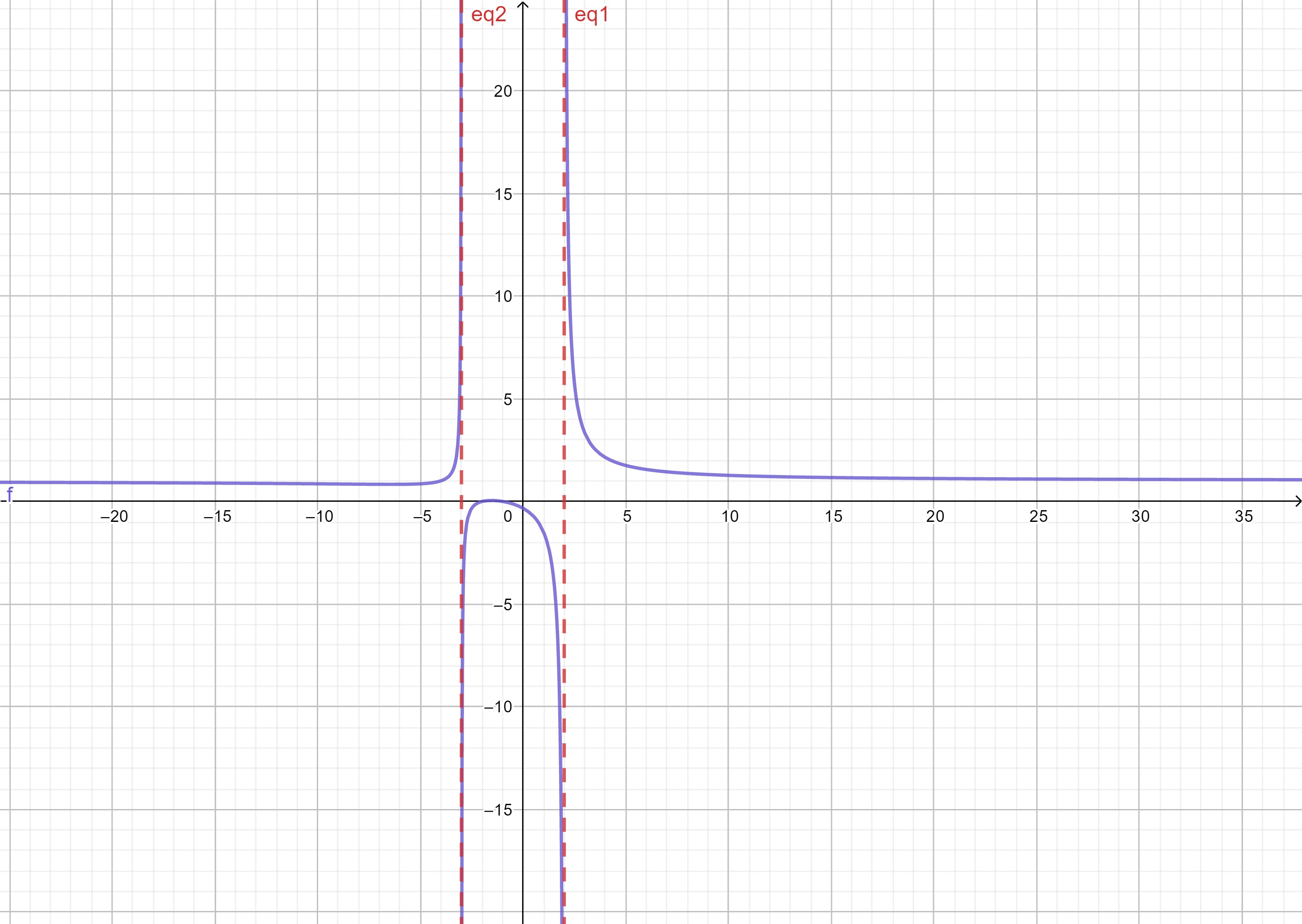
ภาพที่ 23 กราฟฟังก์ชัน [(x + 1)(x + 2)] / [(x – 2)(x + 3)]

          ข้อสังเกตที่พบจากตัวอย่างทั้งสามคือ ในกรณีที่ฟังก์ชันเชิงสัดส่วนสามารถลดรูปเป็นนิพจน์พีชคณิตทั่วไปดังตัวอย่างที่ 16 พฤติกรรมของฟังก์ชันจะมีพฤติกรรมแบบเดียวกันฟังก์ชันที่ลดรูปแล้วแต่ไม่สามารถหาค่าได้ ณ ตำแหน่งที่ไม่นิยาม แต่สำหรับตัวอย่างที่ 15 และ 17 เราพบว่าฟังก์ชันมีแนวโน้มลู่ออกแต่อาจเป็นไปในทิศทางเดียวกันหรือต่างทิศทางกันก็ได้เช่นกราฟ 1 / (x-1)² เป็น

• การแยกเศษส่วนย่อย

          พิจารณาการบวกกันของฟังก์ชันพหุนามเชิงสัดส่วน

         A / (x – r) + B / (x – s) = [(A+B)x + (As+Br)] / [(x-r)(x-s)]

        นั้นคือฟังก์ชันเชิงสัดส่วนในรูป (ax + b) / (x-r)(x-s) สามารถแยกได้เป็นผลบวกของ A / (x – r) + B / (x – s)

        สมมติให้  (ax + b) / (x – r)(x – s)  =  A / (x – r) + B / (x – s)

       นำ (x – r)(x – s) คูณตลอดจะได้

            (ax + b) = A(x – s) + B(x – r)

                 แทนค่า x = s จะได้

           as + b = B(s-r)

      พบว่า B = (as + b) / (s – r) จากนั้นแทนค่า x = r จะได้

           ar + b = A(r-s)

      พบว่า A = (ar + b) / (r-s)

ฟังก์ชันเชิงสัดส่วนที่ตัวส่วนสามารถแยกตัวประกอบได้อาจสามารถเขียนใหม่ได้ในรูปผลบวก เราเรียกวิธีการนี้ว่าการแยกเศษส่วนย่อย

ตัวอย่างที่ 18 จงแยกเศษส่วนย่อยของ (5x – 19) / (x² – 5x + 6)

          (5x – 19) / (x² – 5x + 6) = (5x – 19) / (x – 2)(x – 3)

          ในที่นี้ a = 5, b = -19, r = 2 และ s = 3 จะได้

          A = (5x2 – 19) / (2 – 3) = 9 และ B = (5x3 – 19) / (3 – 2) = -4

ดังนั้น  (5x – 19) / (x² – 5x + 6) = 9 / (x – 2) – 4 / (x – 3)

แหล่งที่มา

Donald L.H. and James F.H. (1998). Data, Statistics and decision models with excel. Anabella Breakey.

John B. (2007). Engineering mathematics. Elsevier Ltd.