สถานการณ์

          สปริงตั้งอยู่ในแนวดิ่ง มีค่านิจสปริงเป็น k N/m ปล่อยก้อนมวล M จากระยะสูง / วัดจากปลายด้านบนของสปริงก้อนมวล M ตกลงที่ปลายสปริงและอัดสปริงลงไป อยากทราบระยะยุบสูงสุดของสปริง

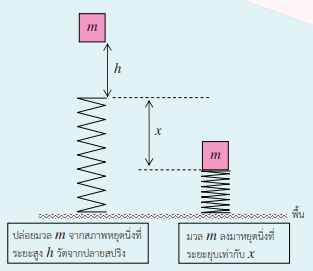
เนื้อความ

          หากถามคำถามนี้กับนิสิต นักศึกษา หรือนักเรียนมัธยมปลายจำนวนมาก (หรือแม้แต่คุณครู ก็จะได้คำตอบที่ว่า ระยะ x ดังกล่าวสามารถหาได้จากความสัมพันธ์   ซึ่งเป็นคำตอบที่ผิด เพราะ?

ก่อนที่ท่านจะอ่านบรรทัดถัดไป อยากให้ละสายตาจากบทความนี้และลองคิดหาคำตอบ

          เราอาจโต้แย้งว่าคำตอบนี้ผิดได้ด้วยเหตุผลง่าย ๆ ที่ว่าทำไมระยะ x จึงไม่ขึ้นกับตำแหน่งที่ปล่อยวัตถุ (ไม่มีค่า / ในคำตอบ) เพราะเราทุกคนมีประสบการณ์ตรงกันว่า ยิ่งปล่อยสูงเท่าใด สปริงก็ต้องยุบเยอะขึ้นเท่านั้น (ถ้า h มาก ค่า x ต้องมากตามไปด้วย)

          แต่ความสัมพันธ์  kx = mg ก็ไม่น่าจะผิดเพราะเมื่อแรงสมดุล วัตถุก็ควรหยุดนิ่ง....ไม่ใช่หรือ ?

          ผิดครับ เมื่อแรงสมดุล วัตถุจะมีความเร่งเท่ากับศูนย์ซึ่งแปลความหมายได้เพียงว่า ก่อนหน้าที่วัตถุจะเข้าสู่สมดุลแรงเป็นอย่างไร เมื่อเกิดสมดุลแรง วัตถุก็เพียงรักษาสภาพการเคลื่อนที่เดิมไว้ชั่วครู่ จนกว่าจะไม่เกิดสมดุลแรง ในสถานการณ์นี้ ขณะที่ก้อนมวลกำลังเคลื่อนที่ลงมา ปริมาณ kx ก็กำลังเพิ่มขึ้นเข้าใกล้ค่า ทg เข้าไปทุกขณะ แต่แรงลัพธ์ก็ยังมีทิศลงอยู่ เมื่อเกิดเงื่อนไข kx = mg ขึ้น ก้อนมวลดังกล่าว "กำลังเคลื่อนที่" อยู่ ดังนั้นก้อนมวลนี้จะไม่หยุด แต่จะยังคงเคลื่อนที่ต่อไป (รักษาสภาพเฉื่อย) ดังนั้นระยะยุบสูงสุดของสปริงจึงไม่ใช่ปริมาณ mg/k แต่มีค่ามากกว่านี้

แล้วเราจะหาคำตอบของสถานการณ์นี้อย่างไร ?

          ใช่แล้วครับ โดยสมมติว่ามีการอนุรักษ์พลังงาน โดยให้ตำแหน่งต่ำสุดของก้อนมวลเป็นตำแหน่งอ้างอิงสำหรับคำนวณพลังงานศักย์โน้มถ่วง และให้สมมติว่าเกิดการเปลี่ยนรูปพลังงานศักย์โน้มถ่วงเป็นพลังงานศักย์ยืดหยุ่นในสปริงอย่างสมบูรณ์ (ไม่เกิดพลังงานในรูปอื่นขึ้น) ซึ่งเขียนเป็นความสัมพันธ์ได้ว่า

เพื่อสะดวกต่อการพิจารณาในลำดับถัดไป

          จากสมการ (3) จะเห็นว่าคำตอบที่ได้มีความสมมาตรรอบตำแหน่ง    ซึ่งเป็นตำแหน่งของสมดุลแรง และเคลื่อนที่ลงมาจากตำแหน่งดังกล่าวอีกเป็นระยะ    (ข้อมูลเพิ่มเติม สังเกตว่าค่า R จากสมการ (4) จะมีค่าเป็นบวกเสมอดังนั้น  จึงมีค่าเป็นบวกเสมอ ซึ่งทำให้การพิจารณาง่ายขึ้นในกรณีที่ R น้อยกว่าศูนย์ รากที่สองของ R จะกลายเป็นจำนวนเชิงซ้อน ซึ่งการพิจารณาจะยุ่งยากมากกว่านี้)

เรามาลองพิจารณาในกรณีต่อไปนี้

กรณีที่ 1 ถ้า h = 0

กรณีที่ 2 ถ้า h > 0

          การหาคำตอบของ 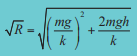  ในรูปของตัวแปรกระทำได้ค่อนข้างยาก แต่ถึงกระนั้นจากรูปคำตอบเราอาจเขียนได้ว่า  อย่างแน่นอน  (คือ  จะไม่น้อยไปกว่าค่า mg/k แน่ ๆ ) ซึ่งทำให้เราบรรยายสภาพการเคลื่อนที่ได้ว่า ถ้าปล่อยมวลสูง h จากตำแหน่งปลายของสปริง และถ้าสมมติว่าก้อนมวลนั้นติดแน่นกับปลายสปริงตลอดเวลา สภาพการเคลื่อนที่จะเป็นการสั่นรอบตำแหน่งสมดุลแรง  เช่นเดิม แต่แอมพลิจูดการสั่นจะเปลี่ยนเป็น   นั่นคือสั่นแรงขึ้นด้วยระยะ   ดังนั้นตำแหน่งต่ำสุดที่ก้อนมวลลงไปได้คือ   (แต่ถ้าก้อนมวลไม่ติดกับปลายสปริง ก้อนมวลก็จะเคลื่อนที่กลับมาที่ตำแหน่งที่ปล่อย)

สรุป

          สปริงตั้งอยู่ในแนวดิ่ง มีค่านิจสปริงเป็น k N/m ปล่อยก้อนมวล M จากระยะสูง h วัดจากปลายด้านบนของสปริง ก้อนมวล m ตกลงที่ปลายสปริงและอัดสปริงลงไป สปริงจะหดสั้นมากที่สุดเป็นระยะเท่ากับ   ถ้ามวลติดไปกับปลายสปริงหลังสัมผัส และเราอาจเขียน  เราจะได้ว่าก้อนมวลสั่นอยู่ในช่วง 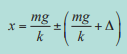  นั่นคือเป็นการสั่นรอบ ๆ ตำแหน่ง  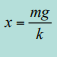ด้วยแอมพลิจูด  

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/