เรขาคณิตหลายมิติ
ทรงกลมในหลายมิติ
เมื่อกล่าวถึงทรงกลม หลายคนจะคุ้นเคยกับก้อนวัตถุโค้งเรียบ เช่นลูกบอล หรือลูกโลก เป็นต้น ทรงกลมในความหมายนี้
เป็นวัตถุที่อยู่ในอวกาศสามมิติ ในทางคณิตศาสตร์ ทรงกลมเป็นพื้นผิวสองมิติที่ฝังตัวอยู่ในอวกาศสามมิติ โดยมีนิยามเป็น
เซตของจุดที่อยู่ห่างจากจุดคงที่ (จุดศูนย์กลาง) เป็นระยะทางเท่ากัน ตามความสัมพันธ์ในระบบพิกัดฉาก สำหรับทรงกลม
ที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด
x2+ y2+ z2= R2
โดยที่ R เป็นรัศมีของทรงกลม โดยทั่วไป นิยมเขียนแทน ทรงกลมสองมิติ ด้วย S2
ในรูปแบบเดียวกัน วงกลมจัดเป็นทรงกลม หนึ่งมิติ S' ที่ฝั่งตัวอยู่ในอวกาศสองมิติ โดยมีจุดศูนย์กลางอยู่ที่จุดกำเนิด จะมีสมการเป็น
x2+ y2= R2
ทั้งสองแบบนี้เป็นรูปทรงเรขาคณิตที่คุ้นเคยกันดี แต่นิยามของทรงกลมดังกล่าวนี้สามารถขยายผลไปยัง ทรงกลมมิติใด ๆ ได้เช่นเดียวกัน
ทรงกลมศูนย์มิติ
ทรงกลมศูนย์มิติ S0คือ เซตของจุดในอวกาศหนึ่งมิติ ที่อยู่ห่างจากจุดศูนย์กลางเป็นระยะเท่ากัน ตามสมการ
(x - x0)2= R2
หรือ |x - x0| = R
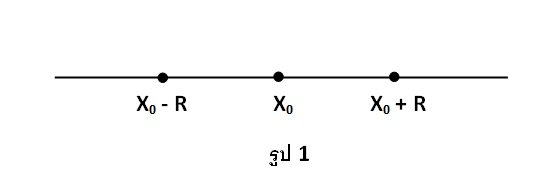
นั่นคือ ทรงกลมศูนย์มิติ ประกอบด้วย 2 จุดคือ x = x0+ R และ x = x0- R ดังรูป 1
ทรงกลมสามมิติ
ทรงกลมสามมิติ S3คือพื้นผิวสามมิติที่ฝังตัวอยู่ในอวกาศสี่มิติ ซึ่งประกอบด้วยจุดที่อยู่ห่างจากจุดศูนย์กลาง (w0, x0, y0, z0) เท่ากัน ตามสมการ
(w - w0)2+ (x - x0)2+ (y - y0)2+ (z - z0)2= R2
จุดในอวกาศสี่มิติ R4ระบุได้ด้วยพิกัดสี่ค่าคือ (w, x, y, z)
มีข้อสังเกตคือ ทรงกลมสามมิติ หมายถึง ทรงกลมที่มีพื้นผิดสามมิติ แต่ตัวทรงกลมเองเป็นก้อนอยู่ในอวกาศสี่มิติ ในทาง
เรขาคณิตตัวทรงกลมหมายถึงจุดที่อยู่บนผิวเท่านั้น สำหรับทรงกลมสองมิติ เช่น ลูกบอล ที่ว่างภายในลูกบอล ไม่ได้นับรวมว่า
เป็นส่วนหนึ่งของทรงกลมเฉพาะจุดที่อยู่ห่างจากจุดศูนย์กลางเท่ากับรัศมีของทรงกลมเท่านั้น ที่นับว่าอยู่ภายในทรงกลม
โดยวิธีการเดียวกันสามารถเขียนสมการที่แสดงทรงกลม n มิติ Snได้เป็นพื้นผิวในอวกาศ n + 1 มิติ Rn+1ที่อยู่ห่างจาก
จุดศูนย์กลาง (y1, ... , yn+1) เป็นระยะเท่ากัน
(x1- y1)2+ ... + (xn+1- yn+1)2= R2
จุดใน Rn+1ระบุได้ด้วยพิกัด (x1, ... , Xn+1)
กลับไปที่เนื้อหา
ระบบพิกัดทรงกลมในสามมิติ
ในอวกาศสามมิติ R3สามารถระบุตำแหน่งของจุดต่าง ๆ ได้ด้วยค่าพักัดสามค่า เช่น (x, y, z) ในระบบพิกัดฉาก นอกจากนี้
ยังสามารถระบุตำแหน่งของจุดใน R3ในระบบพิกัดอื่น ๆ ได้อีกด้วย เช่น ระบบพิกัดทรงกลม และระบบพิกัดทรงกระบอก เป็นต้น
ระบบพิกัดทรงกลมในสามมิติ
พิจารณาจุดใน R3ที่มีพิกัดเป็น (x,y,z) ดังรูป 1 จุด (x,y,z) สามารถ
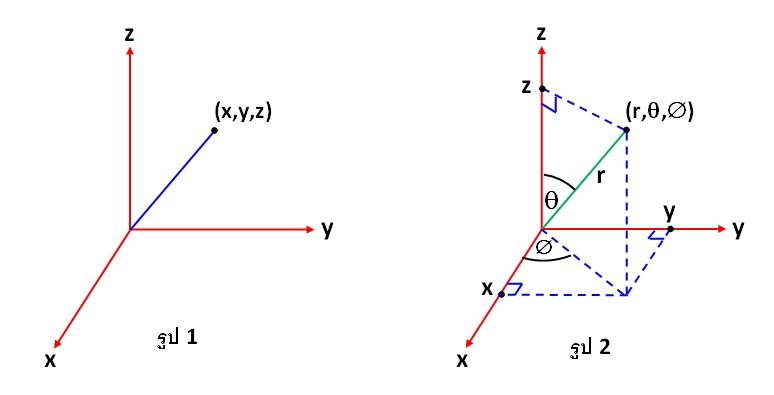
กำหนดให้มีค่าพิกัดในระบบพิกัดทรงกลมได้เป็น (r, θ,Ø) ดังรูป 2 ในที่นี้ r เป็นระยะทางจากจุดกำเนิด (0,0,0)θ เป็นมุมที่วัด
จากแกน z และØ เป็นมุมที่วัดจากแกน x มายังโปรเจกชันของ r บนระนาบ xy
จากรูป 2 จะได้ความสัมพันธ์ระหว่าง พิกัด (x,y,z) และ (r,θ,Ø) เป็น
z = r cosθ -----(1)
x = r sinθ cosØ -----(2)
y = r sinθ sinØ -----(3)
ซึ่งสามารถหาอินเวอร์สได้เป็น
พิสัยของค่าพิกัด (x,y,z) คือ
-∞ < x <∞ , -∞ < y <∞ , -∞ < z <∞
ส่วนค่าพิสัยของพิกัด (r,θ,Ø) หาได้ดังนี้
เนื่องจากจึงได้ r≥ 0
สำหรับØ จะพบว่า 0≤Ø≤ 2Π เนื่องจาก y/x ให้ค่า tanØ ได้ทุกค่าในช่วง (-∞,∞) สำหรับθ จะได้ว่า 0≤θ≤Π
เนื่องจาก cos-1มีค่าอยู่ในช่วง [0,Π] จึงสรุปได้ว่า ในพิกัดทรงกลม
r≥ 0 , 0≤θ≤Π, 0≤Ø≤ 2Π
การใช้พิกัดทรงกลมทำให้เขียนสมการบางอย่างได้ง่ายขึ้น เช่น วงกลมรัศมี R และมีจุดศูนย์กลางอยู่ที่จุดกำเนิดมีสการใน
ระบบพิกัดฉากเป็น
x2+ y2+ z2= R2
เมื่อใช้ความสัมพันธ์ (1), (2) และ (3) จะได้สมการในรูปแบบง่าย ๆ คือ
r = R
กลับไปที่เนื้อหา
ระบบพิกัดทรงกลมใน n มิติ
พิจารณาอวกาศ Rnที่ระบุตำแหน่งของจุดใด ๆ ด้วยพิกัด n ค่า (x1, ... , xn) ในที่นี้ จะแสดงวิธีการระบุตำแหน่งของจุดใ Rnด้วย
พิกัดทรงกลม ให้จุด P(x1, ... , xn) อยู่ห่างจากจุดกำเนิดเป็นระยะ r จะได้ว่า
r2= x12+ x22+ ... + xn2-----(1)
ในระบบพิกัดทรงกลม จะใช้ค่า r ร่วมกับมุมอีก n-1 ค่าในการระบุตำแหน่งของจุด P พิกัดเชิงมุม θi, i = 1, ... , n-1 คือพิกัดบน
ทรงกลม n-1 มิติที่มีรัศมี r ดังแสดงในสมการ (1) การเขียนพิกัด (x1, ... , xn) ในรูปของ (r, θ1, ... , θn-1) ทำได้โดยแก้สมการ (1)
ดังนี้ ให้ xn= r cos θ1
จากสมการ (1) จะได้ x12+ ... + (xn-1)2= r2sin2θ1-----(2)
จากนั้นให้ xn-1= r sin θ1cos θ2
จากสมการ (2) จะได้ x12+ ... + (xn-2)2= r2sin2θ1sin2θ2-----(3)
จากนั้นให้ xn-2= r sin θ1sin θ2cos θ3
แทนลงใน (3) จะได้
x12+ ... + (xn-3)2= r2sin2θ1sin2θ2sin2θ3
โดยการทำเช่นเดียวกัน ซ้ำไปเรื่อย ๆ จนถึง x1จะได้ความสัมพันธ์
xn= r cos θ1
xn-1= r sin θ1cos θ2
xn-2= r sin θ1sin θ2cos θ3
•
•
•
x2= r sin θ1... sin θn-2cos θn-1
x1= r sin θ1... sin θn-2sin θn-1
ในลักษณะเดียวกับพิกัดทรงกลมในสามมิติ (r, θ, Ø) สามารถ พิจารณาได้ว่า พิสัยของพิกัด (r, θ1, ... , θn-1) มีค่าเป็น
r ≥ 0 , 0 ≤ θ1≤ Π , 0 ≤ θi≤ Π , i = 2, ... , n-1
เพื่อให้เห็นภาพชัดเจนขึ้น พิจารณาตัวอย่างของพิกัดทรงกลมใน 4 มิติ ดังต่อไปนี้
พิกัดทรงกลมใน 4 มิติ
พิกัดของจุดใน R4ระบุได้ด้วย (w,x,y,z) ในระบบพิกัดฉาก ในระบบพิกัดทรงกลม (r, θ, Ø, φ) จะได้ว่า
r2= w2+ x2+ y2+ z2
สมการนี้จะเป็นจริงเมื่อให้
z = r cos θ
y = r sin θ cos Ø
x = r sin θ sin Ø cos φ
w = r sin θ sin Ø sin φ
จากความสัมพันธ์ที่ได้ จะพบว่าที่ θ = 0 จะได้ (w, x, y, z) = (0, 0, 0, r) ซึ่งเป็นจุดที่อยู่บนแกน z โดยห่างจากจุดกำเนิดเป็นระยะ
r มุม θ จึงกวาดจาก แกน +z ไปยังง -z เนื่องจาก 0 ≤ θ ≤ Π มุมที่เหลือ คือ Ø และ φ จะกวาดไปบนอวกาศ สามมิติ ที่เขียนใน
ระบบพิกัดทรงกลม (r sin θ, Ø, φ) ให้สังเกตว่า พิกัดรัศมี มีค่า เป็น r sin θ จึงอาจกล่าวได้ว่า พิกัดทรงกลมใน R4 เกิดจากการ
รวมกัน ของพิกัดทรงกลมในสามมิติ ที่ทุกค่าของ sin θ ที่ 0 ≤ θ ≤ Π
กลับไปที่เนื้อหา
ลูกบาศก์ในหลายมิติ
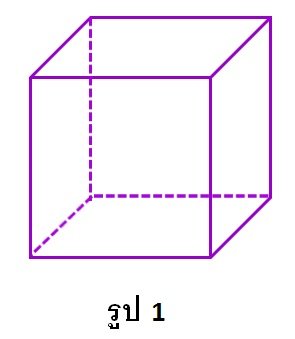
รูปทรงเรขาคณิตที่สำคัญอีกรูปหนึ่งคือ ลูกบาศก์ในสามมิติ ลูกบาศ์กเป็นรูปทรงที่มีความยาวด้านทั้งหมดเท่ากัน โดยมีพื้นผิวทั้ง
หกหน้าเป็นรูปสี่เหลี่ยมจัตุรัส ดังรูป 1
ในบทความนี้ จะกล่างถึงลูกบาศก์ในที่มีมิติมากกว่า 3 โดยจะเริ่มต้นจากจุดศูนย์มิติในรูป 2 จุดศูนย์มิตินี้ อาจพิจารณาได้เป็น
ลูกบาศ์กศูนย์มิติ (ความจริงแล้ว จุดศูนย์มิติ สามารถมองเป็นรูปทรงศูนย์มิติอะไรก็ได้)

หากเลื่อนจุดในรูป 2 ไปทางขวา เป็นระยะหนึ่งหน่วย จะได้เส้นตรงยาวหนึ่งหน่วย ดังรูป 3 ในอีกแง่หนึ่ง สามารถมองว่า
เส้นตรงนี้เป็นลูกบาศก์ในหนึ่งมิติได้ โดยมีหน้าศูนย์มิติสองหน้า (จุดปลายทั้งสองข้าง)
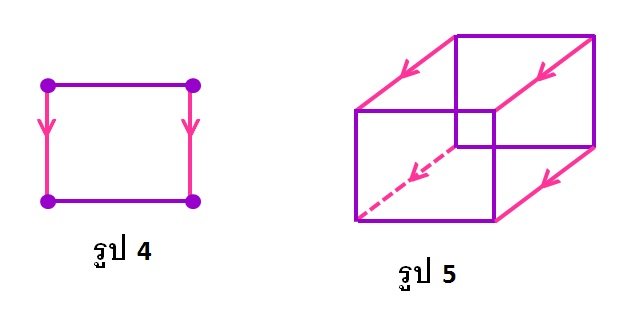
หากเลื่อนเส้นตรงในรูป 3 ในทิศที่ตั้งฉากกับเส้นตรงนี้ เป็นระยะทางหนึ่งหน่วย จะได้รูปสี่เหลี่ยมจตุรัส ดังรูป 4 ในทำนอง
เดียวกัน สามารถมองว่ารูปสี่เหลี่ยมนี้เป็นลูกบาศ์กในสองมิติได้ โดยมีหน้าหนึ่งมิติ ทั้งหมดสี่หน้า (ด้านทั้งสี่ของรูป)
เมื่อเลื่อนสี่เหลี่ยมจตุรัสในรูป 4 ออกไปในทิศทางที่ตั้งฉากกับระนาบของรูปเป็นระยะหนึ่งหน่วย จะได้ลูกบาศก์ในสามมิติ
ดังรูป 5 ลูกบาศก์นี้มีหน้าเป็นพื้นผิวสองมิติทั้งหมดหกหน้า
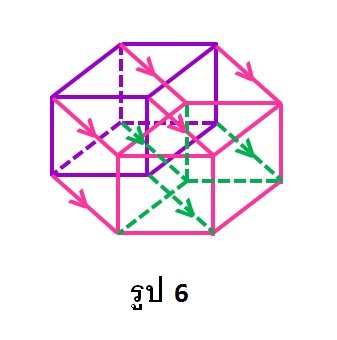
โดยวิธีการเดียวกับที่กล่าวถึงมาทั้งหมดนี้ สามารถนึกภาพของลูกบาศก์ในสี่มิติได้ โดยการเลื่อนลูกบาศก์สามมิติในทิศทางที่
ตั้งฉากกับทิศทางที่ลากสี่เหลี่ยมจตุรัสให้เป็นลูกบาศก์สามมิติ ดังรูป 6 ผลลัพธ์ที่ได้คือ ลูกบาศ์กสี่มิติ ในความเป็นจริง
ลูกบาศก์สี่มิติจะมีหน้าเป็นลูกบาศก์สามมิติ เช่นเดียวกับลูกบาศก์สามมิติ มีหน้าเป็นพื้นผิวสองมิติ โดยจะมีทั้งหมดแปดหน้า
แนวคิดนี้สามารถขยายไปยังลูกบาศก์ n มิติ ใด ๆ ได้ โดยลูกบาศ์ก n มิติ จะมีหน้าเป็นลูกบาศก์ n-1 มิติ ทั้งหมด 2n หน้า
แต่การวาดรูปของลูกบาศก์ที่มีมิติมากกว่าสี่ กระทำได้ยากกว่า
กลับไปที่เนื้อหา



