ฟังก์ชันตรีโกณมิติ

โดย :

ปริญญา การดำริห์

เมื่อ :

วันอาทิตย์, 18 มิถุนายน 2560

Hits

102,290

กราฟของฟังก์ชันตรีโกณมิติ

กราฟของฟังก์ชันตรีโกณมิตินับว่ามีความสำคัญต่อการประยุกต์ใช้งานทางด้านวิทยาศาสตร์เป็นอย่างมาก เนื่องจาก ปริมาณต่าง ๆ ในทางวิทยาศาสตร์ ที่มีการเปลี่ยนแปลงอยู่ในรูปของฟังก์ชันตรีโกณมิติ สามารถทำความเข้าใจได้ง่ายขึ้น เมื่อพิจารณาจากกราฟของฟังก์ชัน

ในบทความนี้ จะพิจารณากราฟของฟังก์ชัน sine และ cosine การนิยามฟังก์ชัน sine และ cosine สามารถทำได้โดยพิจารณาวงกลมรัศมี 1 หน่วย ดังรูป 1

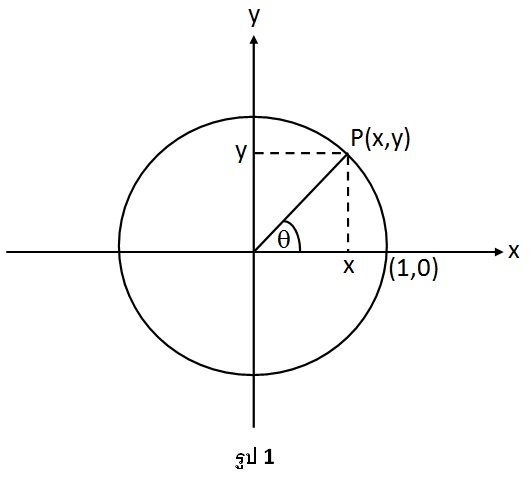
กราฟของฟังก์ชัน sine และ cosine การนิยามฟังก์ชัน sine และ cosine สามารถทำได้โดยพิจารณาวงกลมรัศมี 1 หน่วย

ภาพที่ 1 จะพิจารณากราฟของฟังก์ชัน sine และ cosine การนิยามฟังก์ชัน sine และ cosine สามารถทำได้โดยพิจารณาวงกลมรัศมี 1 หน่วย

มุมθ ภายในวงกลมรัศมี 1 หน่วย จะมีค่าเท่ากับความยาวส่วนโค้งที่รองรับมุมนั้น เนื่องจาก

เมื่อ a แทนความยาวส่วนโค้งที่รองรับมุมθ ในกรณีที่ r = 1 จะได้θ = a

ค่าของมุมθ จะวัดจาก จุด (1,0) ไปยังจุดปลายของส่วนโค้งของวงกลม ในรูป 1 จุด P(x,y) แทนจุดปลายส่วนโค้งที่รองรับมุมθ ฟังก์ชัน sinθ และ cosθ นิยามเป็นค่าพิกัด y และ x ของจุด P ตามลำดับ นั่นคือ

x = cosθ

y = sinθ

ในการเขียนกราฟของฟังก์ชัน sinθ สามารถทำได้โดย นำค่าความยาวส่วนโค้ง (θ) มาใส่บนแกนนอน และ นำค่า พิกัด y ซึ่งให้ค่า sinθ มาใส่บนแกนตั้ง ดังรูป 2

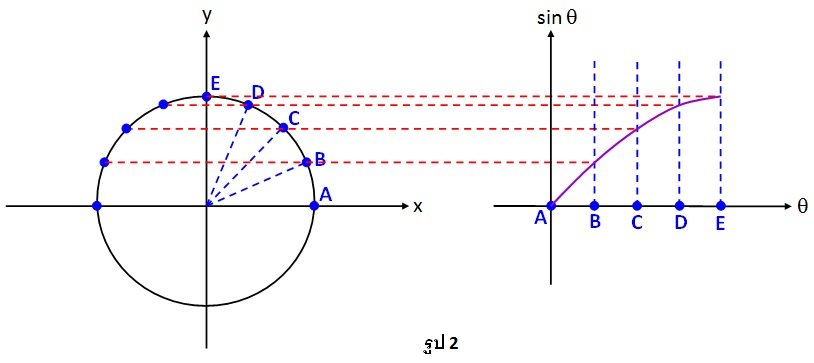
กราฟของฟังก์ชัน sinθ สามารถทำได้โดย นำค่าความยาวส่วนโค้ง (θ) มาใส่บนแกนนอน และ นำค่า พิกัด y ซึ่งให้ค่า sinθ มาใส่บนแกนตั้ง

ภาพที่ 2 กราฟของฟังก์ชัน sinθ สามารถทำได้โดย นำค่าความยาวส่วนโค้ง (θ) มาใส่บนแกนนอน และ นำค่า พิกัด y ซึ่งให้ค่า sinθ มาใส่บนแกนตั้ง

ในรูป 2 แสดงการเขียนกราฟของ sinθ กับθ สำหรับ 0≤θ≤∏/2 โดยการทำเช่นเดียวกันนี้ กับค่าθ อื่น ๆ

จะได้กราฟของ sinθ เป็นดังรูป 3

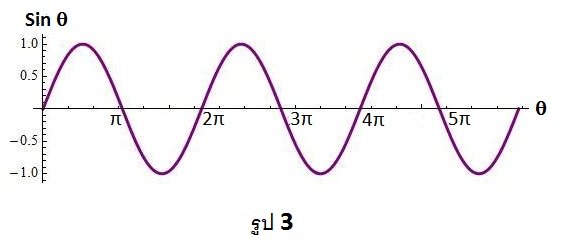
การเขียนกราฟของ sinθ กับθ สำหรับ 0≤θ≤∏/2 โดยการทำเช่นเดียวกันนี้ กับค่าθ อื่น ๆจะได้กราฟของ sinθ

ภาพที่ 3 การเขียนกราฟของ sinθ กับθ สำหรับ 0≤θ≤∏/2 โดยการทำเช่นเดียวกันนี้ กับค่าθ อื่น ๆจะได้กราฟของ sinθ

การเขียนกราฟของฟังก์ชันของ cosθ ก็ทำได้ในแบบเดียวกัน แต่เปลี่ยนจากการนำค่า y มาใส่บนแกนตั้ง เป็นการนำค่า x มาใส่บนแกนตั้ง แทนดังรูป 4 สำหรับ cosθ เมื่อ 0≤θ≤∏/2

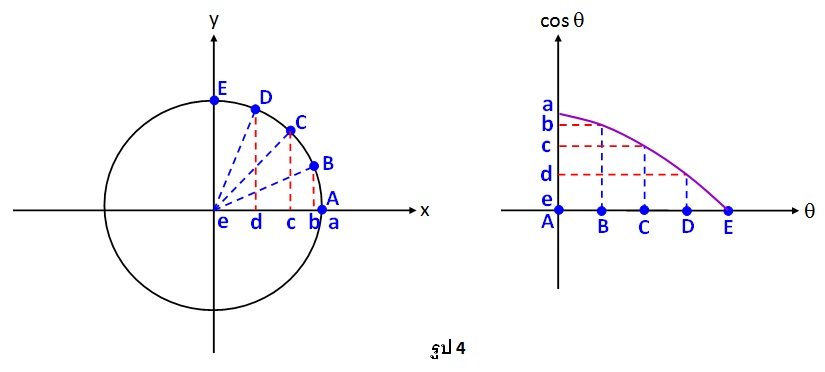
การเขียนกราฟของฟังก์ชันของ cosθ ก็ทำได้ในแบบเดียวกัน แต่เปลี่ยนจากการนำค่า y มาใส่บนแกนตั้ง เป็นการนำค่า x มาใส่บนแกนตั้ง

ภาพที่ 4 การเขียนกราฟของฟังก์ชันของ cosθ ก็ทำได้ในแบบเดียวกัน แต่เปลี่ยนจากการนำค่า y มาใส่บนแกนตั้ง เป็นการนำค่า x มาใส่บนแกนตั้ง

เมื่อเขียนค่าθ อื่น ๆ เพิ่มเข้าไปจะได้กราฟของ cosθ ดังรูป 5

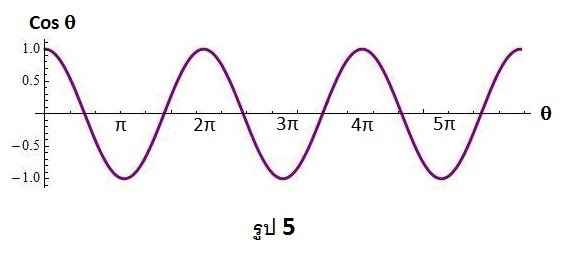
การเขียนกราฟของฟังก์ชันของ cosθ ก็ทำได้ในแบบเดียวกัน แต่เปลี่ยนจากการนำค่า y มาใส่บนแกนตั้ง เป็นการนำค่า x มาใส่บนแกนตั้ง มื่อเขียนค่าθ อื่น ๆ เพิ่มเข้าไปจะได้กราฟของ cosθ

ภาพที่ 5 ต่อจากภาพที่ 4 เมื่อเขียนค่าθ อื่น ๆ เพิ่มเข้าไปจะได้กราฟของ cosθ

กลับไปที่เนื้อหา

สมบัติของกราฟฟังก์ชัน sine และ cosine

ฟังก์ชัน sine และ cosine จัดเป็นฟังก์ชันที่เป็นคาบ กล่าวคือ

sin(x + 2Π) = sin x

และ cos(x + 2Π) = cos x

ในกรณีนี้ จะกล่าวว่า sin x และ cos x เป็นฟังก์ชันที่มีคาบเท่ากับ 2Π ในแง่ของกราฟ ลักษณะของกราฟของ sin x และ cos x

จะซ้ำรูปแบบเดิมเป็นช่วงกว้าง 2Π ดังรูป 1

ในกรณี sin x และ cos x เป็นฟังก์ชันที่มีคาบเท่ากับ 2Π ในแง่ของกราฟ ลักษณะของกราฟของ sin x และ cos x จะซ้ำรูปแบบเดิมเป็นช่วงกว้าง 2Π ดังรูป 1

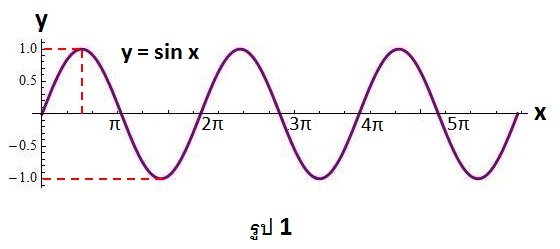
ภาพที่ 6 ในกรณี sin x และ cos x เป็นฟังก์ชันที่มีคาบเท่ากับ 2Π ในแง่ของกราฟ ลักษณะของกราฟของ sin x และ cos x จะซ้ำรูปแบบเดิมเป็นช่วงกว้าง 2Π ดังรูป 1

จากรูป 1 กราฟในช่วง [0,2Π] จะมีลักษณะเหมือนกับกราฟในช่วง [2Π,4Π] เนื่องจากค่าของ -1 ≤sin x ≤1 และ

-1 ≤cos x ≤1จะพบว่ากราฟของ sin x และ cos x มีค่าสูงสุดเป็น 1 และ ค่าต่ำสุดเป็น -1 ขนาดของค่าสูงสุด

รียกว่า แอมพลิจูดของกราฟ

ค่าแอมพลิจูดของกราฟ สามารถเปลี่ยนแปลงได้ โดยคูณฟังก์ชัน sin x หรือ cos x ด้วยค่าคงที่ ตัวอย่างเช่น กราฟ y = 5 sin x

จะมีค่า -5 ≤y ≤5 นั่นคือ มีแอมพลิจูดเท่ากับ 5 เป็นต้น

คาบของฟังก์ชัน อาจมีค่าต่างจาก 2Π ก็ได้ หากมีค่าคงที่คูณอยู่กับ x เช่น กราฟ y = sin 2x จะมีคาบเป็นΠ เนื่องจาก

y(x +Π) = sin 2(x + Π) = sin (2x + 2Π) = sin 2x = y(x)

จากการพิจารณาที่ผ่านมา สามารถสรุปลักษณะกราฟ ของฟังก์ชัน sine ในรูปแบบทั่วไป ได้ดังนี้ พิจารณากราฟของฟังก์ชัน

y = A sin Bx ----(1)

โดยที่ A และ B เป็นจำนวนจริง

กราฟของสมการ (1) มีแอมพลิจูด เท่ากับ |A| เนื่องจาก -|A|≤ y≤ |A| และมีคาบเป็น 2Π/B เนื่องจาก

ในรูปแบบเดียวกัน จะได้ว่ากราฟของฟังก์ชัน

y = A cos BX

มีแอมพลิจูดเป็น (A) และ มีคาบเป็น 2Π/B กราฟของฟังก์ชัน sine และ cosine

แสดงในรูป 2

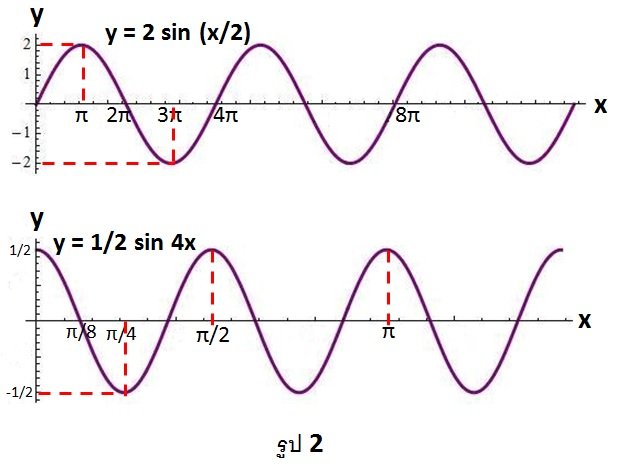
ภาพ ลักษณะของกราฟของ sin x และ cos x ที่มี แอมพลิจูดเป็น (A) และ มีคาบเป็น 2Π/B กราฟของฟังก์ชัน sine และ cosine

ภาพที่ 7 ลักษณะของกราฟของ sin x และ cos x ที่มี แอมพลิจูดเป็น (A) และ มีคาบเป็น 2Π/B กราฟของฟังก์ชัน sine และ cosine

กลับไปที่เนื้อหา

การเขียนกราฟของฟังก์ชัน sine และ cosine

โดยใช้แนวคิดของการเลื่อนกราฟ สามารถเขียนกราฟของฟังก์ชันที่อยู่ในรูป

y = A sin (Bx -C) + k ----(1)

ได้ดังนี้ ให้ h = C/B สามารถเขียนสมการ (1) ได้เป็น

y-k = A sin (B(x-h))

ซึ่งเป็นสมการ y' = A sin Bx' ที่เกิดจาก การเลื่อนจุดกำเนิดจาก (0,0) ไปยัง (h,k) ดังรูป 2

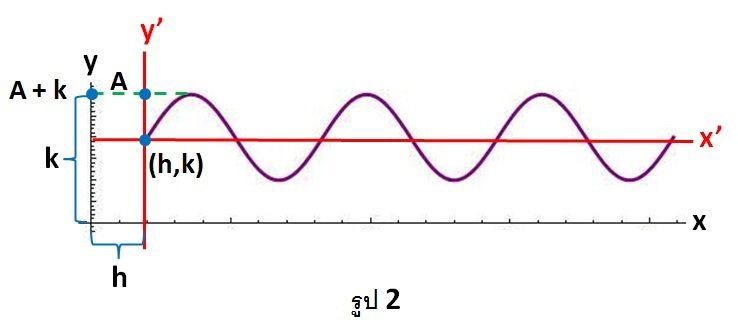
สมการ y' = A sin Bx' ที่เกิดจาก การเลื่อนจุดกำเนิดจาก (0,0) ไปยัง (h,k)

ภาพที่ 8 ภาพสมการ y' = A sin Bx' ที่เกิดจาก การเลื่อนจุดกำเนิดจาก (0,0) ไปยัง (h,k)

มีข้อควรสังเกต คือ กราฟของสมการ (1) ยังคงมีคาบเท่ากับ 2Π/B

สำหรับกราฟของ ฟังก์ชัน cosine สามารถเขียนได้ โดยใช้สมบัติ

cosθ = sin (θ + Π/2)

จึงได้ว่ากราฟของ y = A cos Bx = A sin (Bx + Π/2) เกิดจากการเลื่อนกราฟของ y = A sin Bx ไปทางซ้ายเป็นระยะ Π/2 เนื่องจากในกรณีนี้ h = -Π/2 ดังแสดงในรูป 3

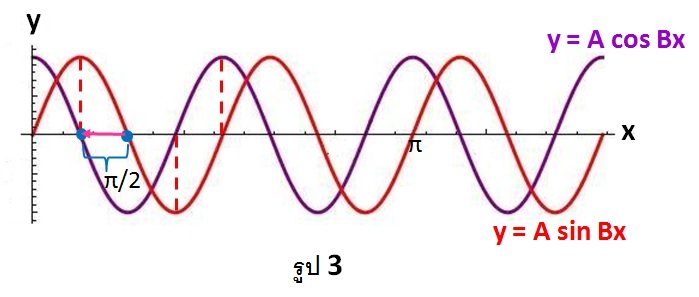
ภาพกราฟของ y = A cos Bx = A sin (Bx + Π/2) เกิดจากการเลื่อนกราฟของ y = A sin Bx ไปทางซ้ายเป็นระยะ Π/2 เนื่องจากในกรณีนี้ h = -Π/2