ช่วงและการแก้อสมการ ช่วงและการแก้อสมการ
1. ช่วง
ถ้าเราลากเส้นตรงเส้นหนึ่งแล้วเลือกจุดใดจุดหนี่งบนเส้นตรงนั้นเป็นเป็นจุดแทนจำนวนศูนย์ (0) หลังจากนั้นเลือกหน่วยความยาว แล้วระบุจุดบนเส้นตรงนี้ที่ระยะห่าง 1, 2, 3, … หน่วยทางขวามือของศูนย์เป็นจำนวน 1, 2, 3, … ตามลำดับ และในทำนองดียวกัน ระบุจุดบนเส้นตรงนี้ที่ระยะห่าง 1, 2, 3, … หน่วยทางซ้ายมือของศูนย์เป็นจำนวน -1, -2, -3, … ตามลำดับ
นักคณิตศาสตร์ ถือว่า จำนวนจริงทุกจำนวนจะสามารถเขียนแทนด้วยจุดบนเส้นจำนวนนี้ และในทางตรงกันข้าม ทุกจุดบนเส้นจำนวนนี้สามารถเขียนแทนด้วยจำนวนจริงได้ เรียกเส้นตรงแบบนี้ว่า “เส้นจำนวน”
ช่วงแต่ละช่วง หมายถึง เซตของจำนวนจริงใดๆที่เป็นสับเซตของจำนวนจริงทั้งหมด R ทุกสมาชิกในช่วงช่วงนี้จะสามารถเขียนแทนด้วยจุดบนเส้นจำนวนได้ โดยเราสามารถแบ่งช่วงออกเป็น 4 แบบดังนี้

กลับไปที่เนื้อหา
การแก้อสมการ คือ การหาเซตคำตอบของอสมการ ซึ่ง ในที่นี้จำเป็นต้องใช้คุณสมบัติการไม่เท่ากันของจำนวนจริงและ ความรู้พื้นฐานเกี่ยวกับช่วง ในที่นี้จะแบ่งการแก้อสมการออกเป็นหลายๆรูปแบบดังนี้
รูปแบบที่1การแก้อสมการกำลังหนึ่งอย่างง่าย p(x) < q(x)
การแก้อสมการประเภทนี้สามารถทำได้คล้ายๆกันกับการแก้สมการ โดยข้อแตกต่างจะมาจากการที่คำตอบของอสมการนั้นจะเป็นช่วงของจำนวนจริงแทน ยกตัวอย่างเช่น
จงแก้อสมการต่อไปนี้ 3x – 2 < 2x + 5
วิธีทำ xxxxxx3x – 2 < 2x + 5
xxxxxxxxxx 3x – 2x < 5 + 2
xxxxxxxxxxxxxxxxx x < 7
ดังนั้นเซตคำตอบคือ (–∞, 7)
ข้อสังเกตจะเห็นได้ว่า ขั้นตอนการแก้อสมการนี้เหมือนกันการแก้สมการ ข้อแตกต่างเพียงแค่เปลี่ยน x = 7 ไปเป็น x < 7
รูปแบบที่2การแก้อสมการกำลังหนึ่งโดยทั่วไป p(x) < q(x) < r(x)
การแก้อสมการรูปแบบนี้ให้ทำการแปลงสมการให้เป็นรูปแบบใหม่ก่อนคือ p(x) < q(x) และ q(x) < r(x) เพื่อให้เห็นภาพชัดเจนลองพิจารณาตัวอย่างต่อไปนี้
จงแก้อสมการต่อไปนี้ 3x – 2 ≤ 2x + 5 < 5x – 6
วิธีทำจะได้ nnnnnnnnnn3x – 2 ≤ 2x + 5 และ 2x + 5 < 5x – 7
3x – 2x ≤ 5 + 2 และ 5 + 7 < 5x – 2x
x ≤ 7 และ 4 < x
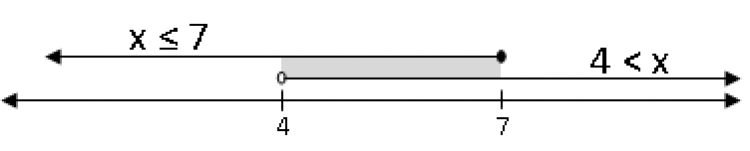
ดังนั้น เซตคำตอบของอสมการคือ (–∞, 7] ∩(4, ∞) = (4, 7]
รูปแบบที่3การแก้อสมการกำลังมากกว่าหนึ่ง
การแก้อสมการที่มีกำลังมากกว่าหนึ่ง มีขั้นตอนดังนี้
1. จัดรูปของสมการให้ข้างใดข้างหนึ่งของสมการเป็นศูนย์ และจัดอีกข้างของสมการให้อยู่ในรูปผลคูณหรือผลหารโดยการแยกตัวประกอบอย่างเช่น
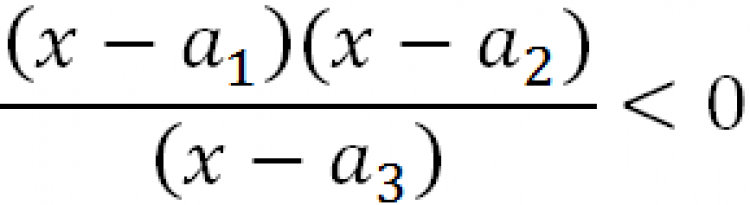
2. นำค่าวิกฤตทั้งหมดที่ได้มาไปเขียนไว้ในเส้นจำนวน ยกตัวอย่างเช่น
![]()
3. เลือกช่วงที่ค่า x ทำให้อสมการเป็นจริงโดยการเขียนช่วงที่ทำให้อสมการมีค่ามากกว่าศูนย์ (+) และ น้อยกว่าศูนย์ (-) จากขวามือไปซ้ายมือตามลำดับ เช่น
![]()
เพื่อให้เห็นภาพและเข้าใจได้ง่ายขึ้น ลองพิจารณาตัวอย่างดังต่อไปนี้
จงแก้อสมการต่อไปนี้ x3– 2x2< x – 2
วิธีทำ 1. เขียนอสมการใหม่ได้เป็น x3– 2x2– x + 2 < 0
2. แยกตัวประกอบได้ดังนี้ (x + 1)(x – 1)(x – 2) < 0
3. เขียนค่าวิกฤตบนเส้นจำนวนได้ดังนี้
![]()
ดังนั้นเซตคำตอบของอสมการคือ (–∞, -1] ∩(1, 2)
รูปแบบที่4การแก้อสมการกำลังมากกว่าหนึ่งในกรณีที่มีตัวประกอบซ้ำ
การแก้สมการรูปแบบนี้สามารถแยกเป็นสองกรณีคือ
![]()
ในกรณีที่nเป็นจำนวนเต็มบวก เราสามารถเขียนอสมการใหม่ได้เป็น(x-a1)(x-a3) ≤ 0
ในกรณีที่nเป็นจำนวนเต็มลบ เราสามารถเขียนอสมการใหม่ได้เป็น (x-a1)(x-a3) ≤ 0 และ x ≠a2
![]()
ในกรณีที่ n เป็นจำนวนเต็มบวก เราสามารถเขียนอสมการใหม่ได้เป็น(x-a1)(x-a2)(x-a3) ≤ 0
ในกรณีที่ n เป็นจำนวนเต็มลบ เราสามารถเขียนอสมการใหม่ได้เป็น (x-a1)(x-a2)(x-a3) ≤ 0และ x ≠ a2
![]()
วิธีทำจะได้
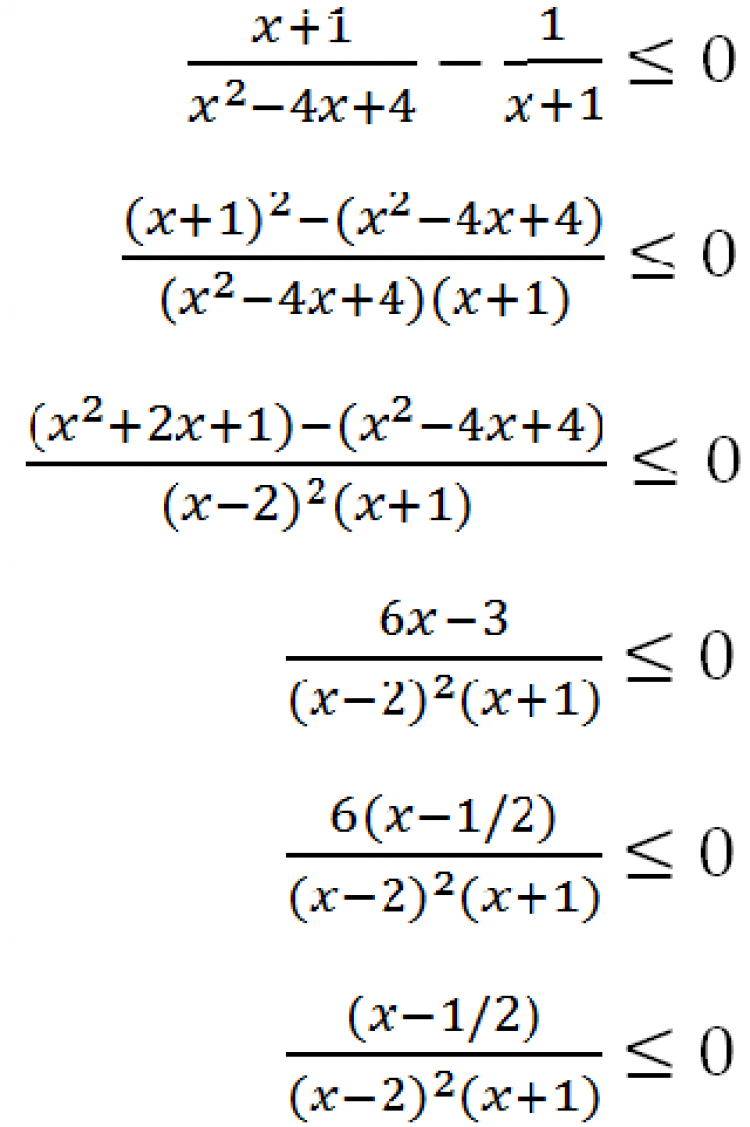
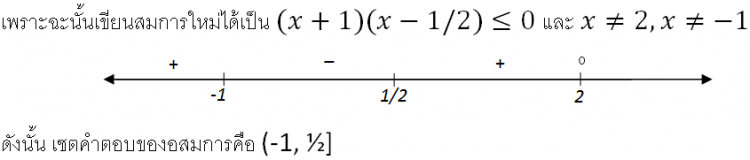
กลับไปที่เนื้อหา
การแก้อสมการที่มีค่าสัมบูรณ์สามารถแยกพิจารณาตามลักษณะของอสมการได้ดังนี้
รูปแบบที่1การใช้คุณสมบัติของจำนวนจริงที่มีค่าสัมบูรณ์ในการแปลงอสมการ
แบ่งได้เป็นสองกรณีคือ
- |y| > k สามารถแปลงได้เป็น y < -k หรือ y > k
- |y| < k สามารถแปลงได้เป็น -k < y < k
ตัวอย่างจงแก้อสมการ |2x - 3| < x + 7
วิธีทำเขียนอสมการใหม่ได้เป็น -(x + 7) < 2x - 3 < x + 7
vvvvแก้อสมการตามปกติ จะได้
-(x + 7) < 2x - 3 และ2x - 3 < x + 7
-4 < 3x และx < 10
-4/3 < x และx < 10

ดังนั้น เซตคำตอบของอสมการคือ (-4/3, 10)
__________________________________________________________________________________________________________________
รูปแบบที่2 ใช้คุณสมบัติยกกำลังสองทั้งสองข้างของอสมการได้ดังนี้
- |p(x)| < |q(x)| สามารถแปลงอสมการได้เป็น p2(x) < q2(x)
- |p(x)| > |q(x)| สามารถแปลงอสมการได้เป็น p2(x) > q2(x)
ตัวอย่าง จงแก้อสมการต่อไปนี้ |2x – 3| ≥ |x – 4|
วิธีทำ ยกกำลังสองทั้งสองข้างของอสมการจะได้
(2x – 3)2 ≥ (x – 4)2
(2x – 3)2 – (x – 4)2 ≥ 0
4x2 – 12x + 9) – (x2 – 8x + 16) ≥ 0
3x2 – 20x – 7 ≥ 0
(3x – 1) (x + 7) ≥ 0

ดังนั้น เซตคำตอบของอสมการคือ (–∞,–7] υ [1/3, ∞)
___________________________________________________________________________________________
รูปแบบที่3 การใช้คุณสมบัติของอสมการ |a + b| < |a| + |b| ก็ต่อเมื่อ ab < 0
จากคุณสมบัตินี้ เราสามารถเขียนอสมการใหม่จาก |p(x) + q(x)| < | p(x) | + | q(x) |ไปเป็น p(x) q(x) < 0
ตัวอย่าง จงแก้อสมการต่อไปนี้ |x2 – x + 1| < |2x – 1| + |x2 – 3x + 2|
วิธีทำ เขียนสมการใหม่ได้เป็น
(2x – 1)( x2 – 3x + 2) < 0
(2x – 1) (x – 1) (x – 2) < 0
![]()
ดังนั้น เซตคำตอบของอสมการคือ (–∞, 1/2] υ (1, 2)
__________________________________________________________________________________________________
รูปแบบที่4 การแยกพิจารณาเป็นช่วงๆ
ในกรณีที่อสมการไม่สามารถแก้ได้โดยการใช้รูปแบบที่กล่าวมาแล้ว
ให้แยกพิจารณาเป็นช่วงๆตามค่าวิกฤตที่หาได้จากนิพจน์ที่มีค่าสัมบูรณ์
เช่น |x – 2| ซึ่งจะได้ค่าวิกฤตเป็น 2 เป็นต้น
เพื่อให้เข้าใจยิ่งขึ้น ลองพิจารณาจตัวอย่างต่อไปนี้
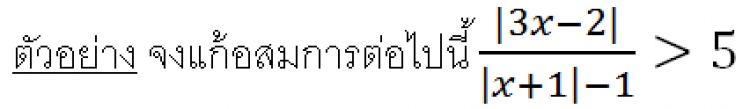
วิธีทำ จากอสมการข้างบน จะเห็นได้ว่า ค่าวิกฤตสำหรับค่าสัมบูรณ์มี 2 ค่า คือ -1 และ 2/3
นำไปเขียนช่วงการพิจารณาในเส้นจำนวนได้ดังนี้
![]()
กรณีที่1 x ≤ -1
สำหรับช่วงการพิจารณานี้ จะเห็นได้ว่า ค่าสัมบูรณ์ของทั้งสองนิพจน์มีค่าน้อยกว่าศูนย์
เพราะฉะนั้น เราจะเขียนอสมการใหม่ได้เป็น
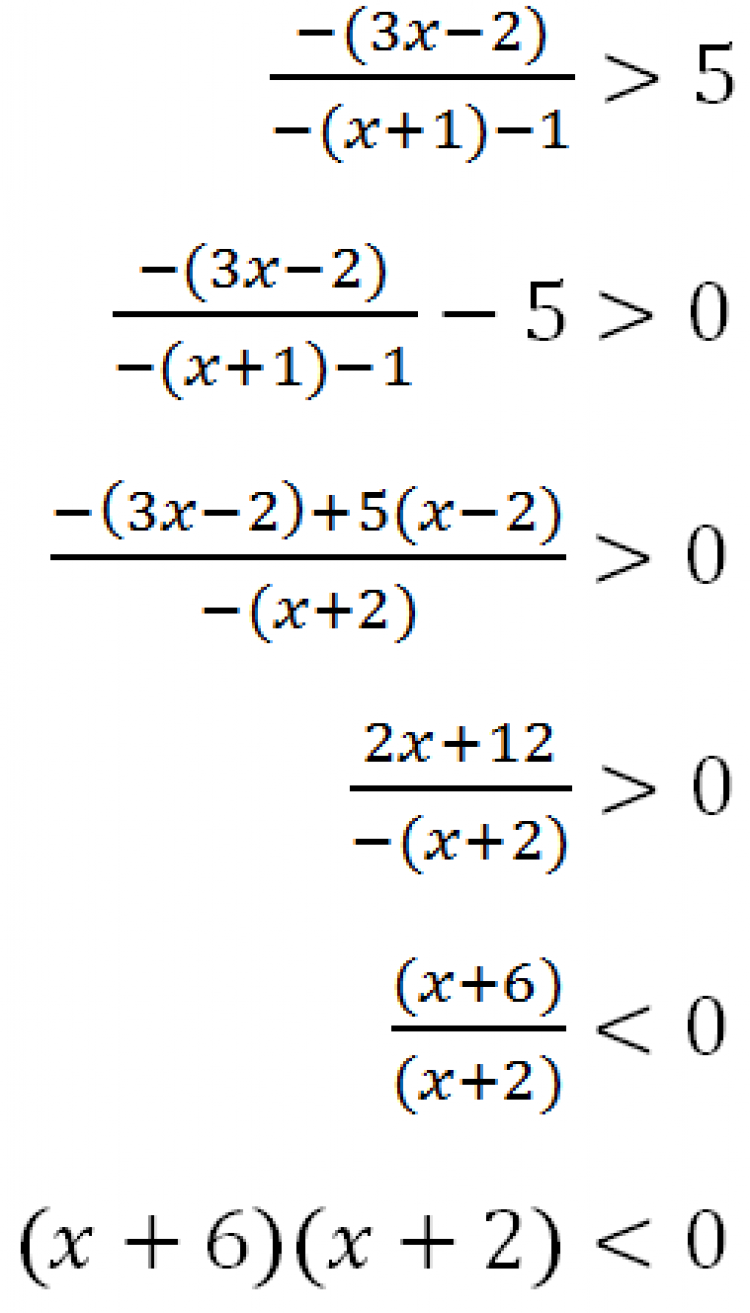
![]()
ดังนั้น เซตคำตอบของอสมการคือ (–∞, –1] ∩ (–6, –2) = (–6, –2)
กรณีที่2 -1< x < 2/3
สำหรับช่วงการพิจารณานี้ เขียนอสมการใหม่ได้เป็น
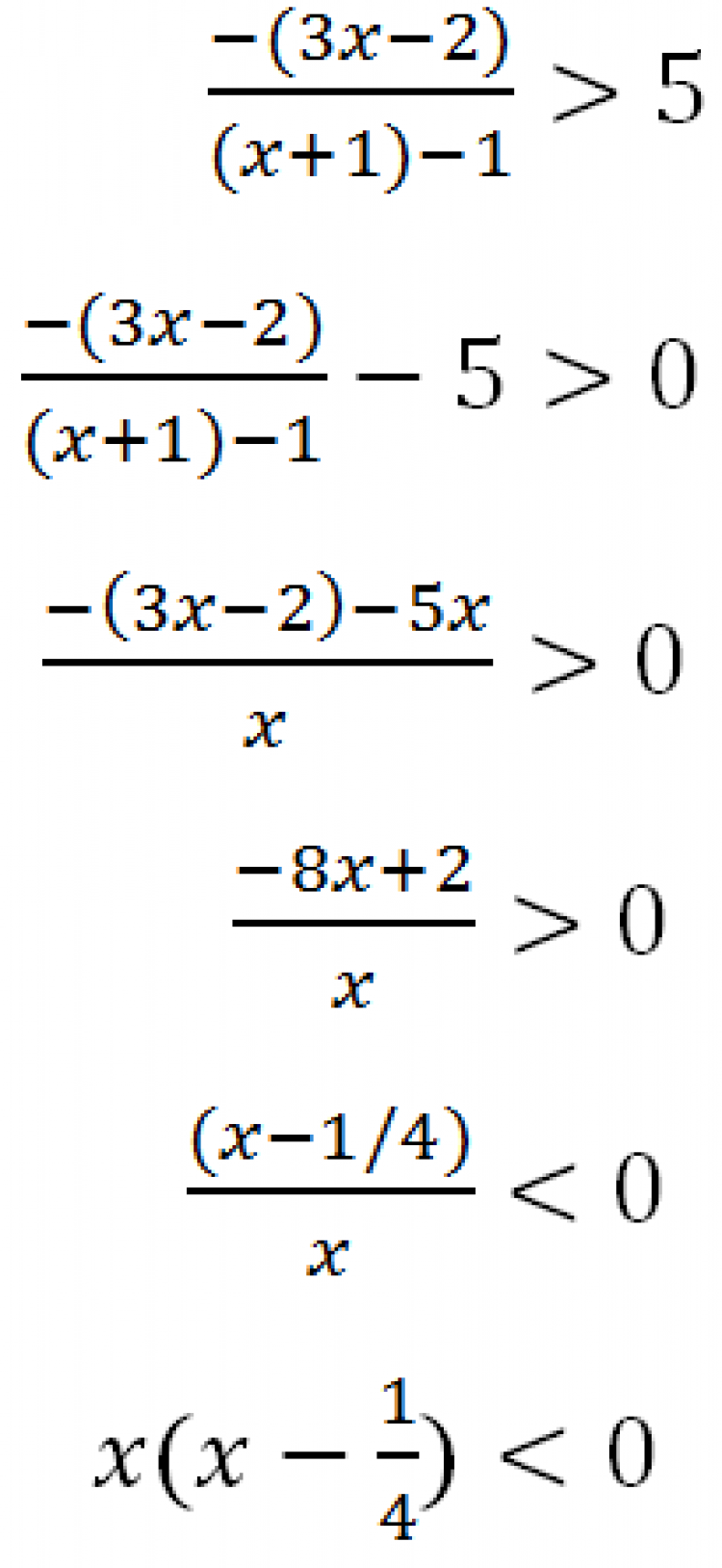
![]()
ดังนั้น เซตคำตอบของอสมการคือ (–1, 2/3) ∩ (0, 1/4) = (0, 1/4)
กรณีที่3 x ≥ 2/3
สำหรับช่วงการพิจารณานี้ เขียนอสมการใหม่ได้เป็น
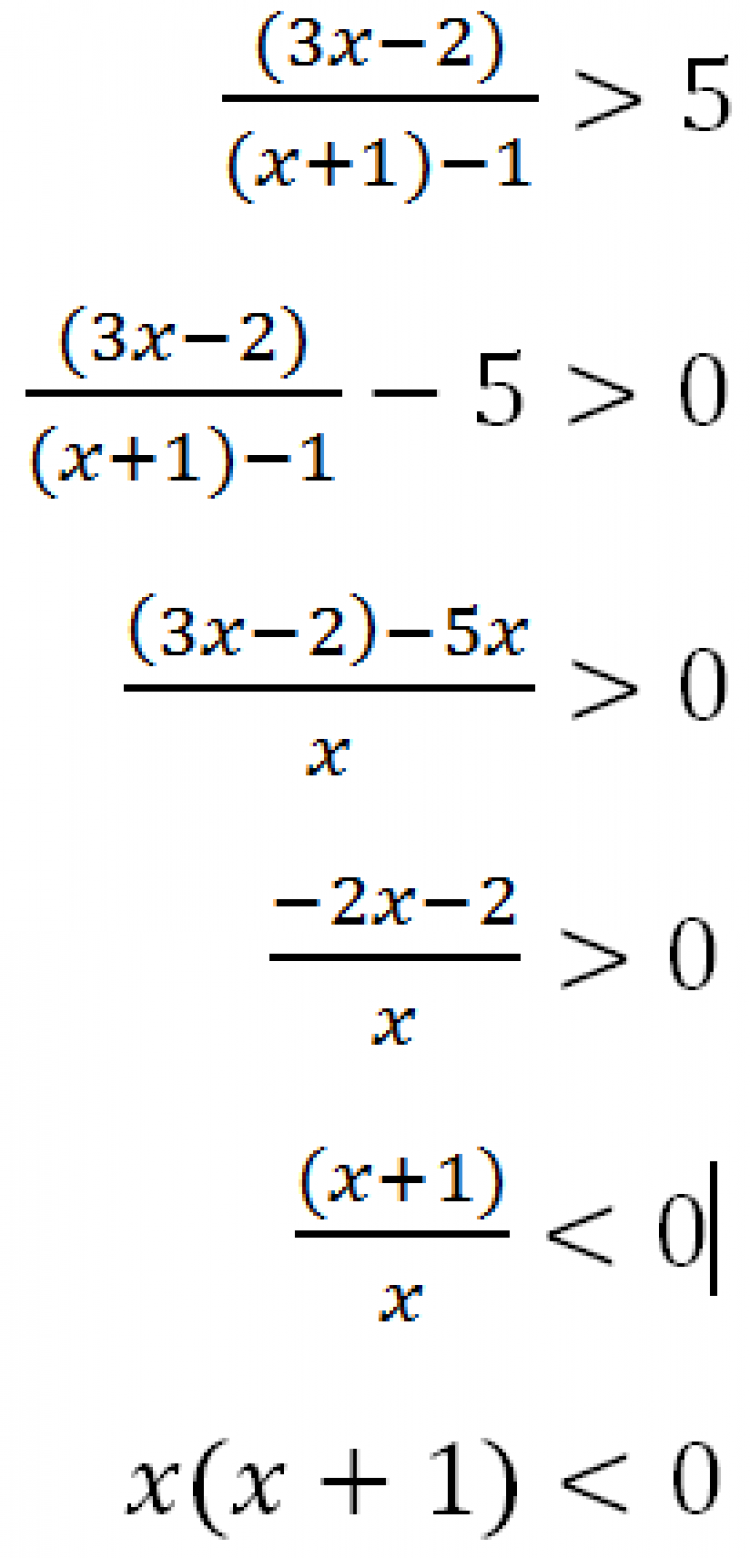
![]()
ดังนั้น เซตคำตอบของอสมการคือ [ 2/3, ∞) ∩ (-1, 0) = Ø
เมื่อรวมทุกคำตอบของทุกช่วงจะได้ (–6, –2] υ (0, 1/4) υ Ø = (–6, –2] υ (0, 1/4)
กลับไปที่เนื้อหา



