เรขาคณิตเบื้องต้นระดับชั้น ม.2-ม.3

ภาพบทเรียนเรขาคณิตเบื้องต้นระดับชั้น ม.2-ม.3
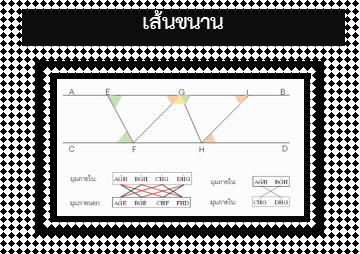
เส้นขนาน
คำว่าคู่ขนานเป็นสื่อถึงสิ่งสองสิ่งที่ไม่บรรจบกัน นั้นหมายความว่าเส้นตรงสองเส้นจะขนานกันก็ต่อเมื่อไม่ว่าเราจะต่อความยาวออกไปเท่าใดเส้นสองเส้นนี้ต้องไม่บรรจบกัน นอกจากนี้เรายังพบข้อสังเกตว่าเส้นตรงสองเส้นที่ขนาดกันระยะห่างระหว่างเส้นจะต้องเป็นค่าคงที่ เรานำแนวคิดนี้มาสร้างเส้นให้ขนานกับเส้นตรงเส้นหนึ่งโดยอาศัยหลักการสร้างรูปเรขาคณิตดังนี้ 1) ในการสร้างเส้นตรงเรากำหนดจุด 2 จุดบนเส้นตรงก็เพียงพอที่จะสร้างเส้นตรง 2) ระยะห่างที่สั้นที่สุดระหว่างเส้นสองเส้นคือเส้นตั้งฉาก จากนั้นเราจะพิจารณาข้อค้นพบที่ได้เมื่อมีเส้นตรงเส้นหนึ่งตัดกับเส้นขนานดังรายละเอียดของกิจกรรมที่ 1 สำหรับกิจกรรมที่ 2 และ 3 จะเป็นการพิสูจน์ข้อค้นพบ และนำทฤษฎีไปแก้ปัญหา
ภาพเส้นขนาน
โดยวีระ ยุคุณธร
กิจกรรมที่ 1 ตั้งข้อคาดการณ์จากการสร้างและการวัดเพื่อนำไปสู่การสรุปทฤษฎีบท
1.1 จงสร้างเส้นตรงโดยที่ เส้นตรง AB ขนานกับ เส้นตรง CD ซึ่งมีเส้นตรง EF ตัดเส้นตรง AB และ CD ที่จุด G และ H ตามลำดับ
วิธีสร้าง เพื่อความสะดวกในการพิจารณาเราจะตัดส่วนของเส้นตรงมาเพื่อพิจารณาโดย
ขั้นตอนที่ 1 สร้างเส้นตรง AB ต่อมาสร้างเส้นตั้งฉากสองเส้นเพื่อกำหนดระยะของจุดสองจุด(การสร้างเส้นตรง) จากนั้นวัดระยะทางของจุดสองจุดให้เท่ากัน(นิยามเส้นขนาน) จะได้ เส้นตรง CD ที่ขนานกับ เส้นตรง AB (รูปที่ 1)
ขั้นตอนที่ 2 ลากเส้นตรง EF โดยที่จุด G เป็นจุดตัดของเส้นตรง EF และ เส้นตรง AB ส่วนจุด H เป็นจุดตัดของเส้นตรง EF และ เส้นตรง CD (รูปที่ 2)
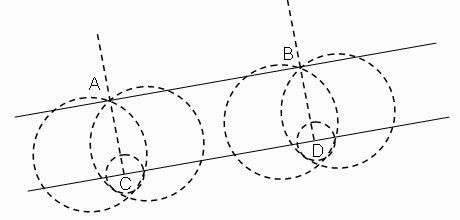
ภาพที่ 1 การสร้างเส้นขนานด้วยสันและส่วนโค้ง
โดย วีระ ยุคุณธร
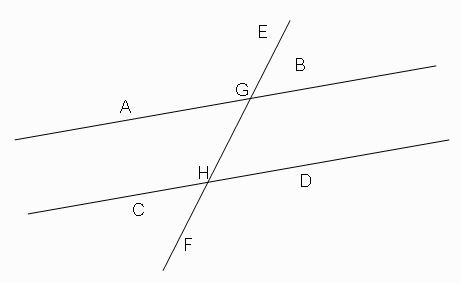
ภาพที่ 2 เส้น EF ตัดเส้นขนาน AB และ CD
โดย วีระ ยุคุณธร
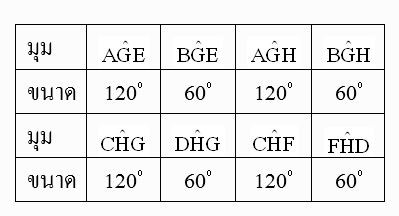
1.2 วัดค่ามุมรอบจุดตัด
ค่ามุมที่เกิดขึ้นแสดงได้ดังตารางต่อไปนี้
ตารางที่ 1 มุมและขนาดของมุมที่เกิดขึ้น (องศา)
1.2.1 แบ่งมุมออกเป็น 2 กลุ่มโดยใช้เกณฑ์มุมที่อยู่ภายในเส้นขนานและมุมที่อยู่ภายนอก
มุมภายใน: มุม AGH, มุม BGH, มุม CHG และ มุม DHG
มุมภายนอก: มุม AGE, มุม BGE, มุม CHF และ มุม FHD
1.2.2 จับคู่มุมภายในที่เท่ากัน
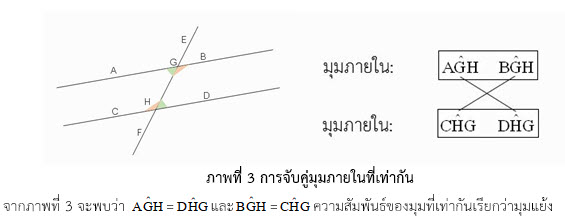
1.2.3 จับคู่มุมภายในและมุมภายนอกที่เท่ากัน

1.3 สรุปข้อคาดการณ์
ข้อคาดการณ์ที่ 1 มุมแย้งภายในเส้นตัดของเส้นขนานมีค่าเท่ากัน
ข้อคาดการณ์ที่ 2 มุมภายและมุมภายนอกที่อยู่บนด้านเดียวกันของเส้นตัดเส้นขนานมีค่าเท่ากัน
กิจกรรมที่ 2 การประยุกต์ใช้ทฤษฎีเพื่อการพิสูจน์
จากปัญหาข้อสอบ o-net ม.3 ปีการศึกษา 2551
จากรูป ถ้าส่วนของเส้นตรง AB ขนานกับ ส่วนของเส้นตรง CD , ส่วนของเส้นตรง EF ขนานกัน ส่วนของเส้นตรง GH และ ส่วนของเส้นตรง FG ขนานกับ ส่วนของเส้นตรง HI จงหาค่า x / 2
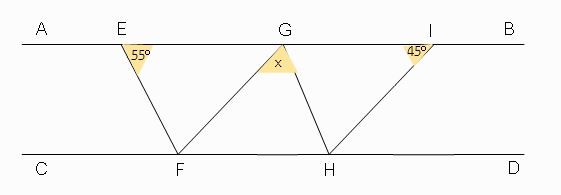
ภาพที่ 5 ข้อสอบโอเนต ม.3/2551
โดย วีระ ยุคุณธร
บทเรียนนี้จะนำเสนอกระบวนการฝึกทักษะการคิดวิเคราะห์เพื่อแก้ปัญหาผ่านการวิเคราะห์เชื่อมโยงข้อมูลและการให้เหตุผลเพื่อสรุป
2.1 วิเคราะห์เชื่อมโยงข้อมูล
จะหาความสัมพันธ์ของ มุม FEG, มุม FGH และ มุม HIG
โจทย์กำหนดมาว่า
(D1) ส่วนของเส้นตรง AB ขนานกับ ส่วนของเส้นตรง CD
(D2) ส่วนของเส้นตรง EF ขนานกับ ส่วนของเส้นตรง GH
(D3) ส่วนของเส้นตรง FG ขนานกับ ส่วนของเส้นตรง HI
พิจารณาความสัมพันธ์
วิเคราะห์: มุม FEG กับ (D1): เป็นมุมภายในของเส้นขนานที่มี EF เป็นเส้นตัด
ข้อค้นพบ: พบว่าสอดคล้องกับทฤษฎีมุมแย้งภายในบนเส้นตัดกับเส้นขนานจึงได้ว่า มุม FEG = มุม EFC
วิเคราะห์: มุม FEG กับ (D2): เป็นมุมภายในของเส้นขนานที่มี AB เป็นเส้นตัด
ข้อค้นพบ: สอดคล้องกับทฤษฎีมุมภายในและมุมภายนอกบนด้านเดียวกันบนเส้นตัดกับเส้นขนานจึงได้ว่า มุม FEG = มุม HGI
วิเคราะห์: มุม FEG กับ (D3): ไม่สัมพันธ์กันตามทฤษฎี
จะได้ดังรูป
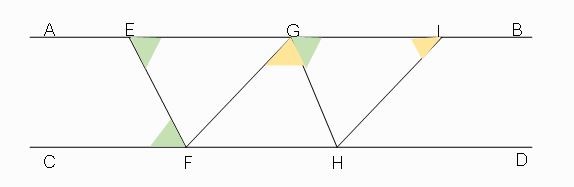
รูปที่ 6 ความสัมพันธ์ของมุม FEG กับข้อความ D1, D2 และ D3
โดย วีระ ยุคุณธร
ในทำนองเดียวกันเมื่อวิเคราะห์ความสัมพันธ์ของมุม HIG กับข้อความ D1, D2 และ D3 จะได้
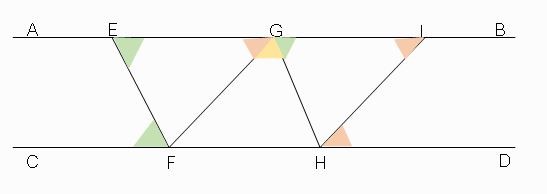
รูปที่ 7 ความสัมพันธ์ของมุม FEG และ HIG กับข้อความ D1, D2 และ D3
โดย วีระ ยุคุณธร
สังเกตได้ว่า มุม FEG + มุม FGH + มุม HGI เท่ากับ 180o
2.2 การให้เหตุผล
จงพิสูจน์ว่า มุม FEG + มุม FGH + มุม HGI เท่ากับ 180o
|
ข้อสรุป |
เหตุผล |
|
มุม FEG = มุม HGB |
มุมภายในและมุมภายนอกระหว่างเส้นขนาน EF กับ GH ที่มี EG เป็นเส้นตัด |
|
มุม HIG = มุม FEG |
มุมภายในและมุมภายนอกระหว่างเส้นขนาน EF กับ GH ที่มี EG เป็นเส้นตัด |
|
มุม FEG + มุม FGH + มุม HGI เท่ากับ 180o |
ผลการรวมมุมทั้งสามเป็นมุมบนเส้นตรง |
กิจกรรมที่ 3 การประยุกต์ใช้ทฤษฏีเพื่อแก้ปัญหา
ถ้าส่วนของเส้นตรง AB ขนานกับส่วนของเส้นตรง CD ส่วนของเส้นตรง EF ขนานกันส่วนของเส้นตรง GH และส่วนของเส้นตรง FG ขนานกับส่วนของเส้นตรง HI แล้วจงหาค่า x/2
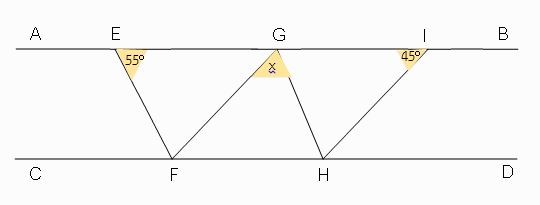
ภาพที่ 5 ข้อสอบโอเนต ม.3/2551
โดย วีระ ยุคุณธร
วิธีทำ
เนื่องจาก FEG และ HGI เป็นมุมภายในและมุมภายนอกบนเส้นตัด EG กับเส้นขนาน EF และ GH จะได้ว่า FEG = HGI = 55o
และ HIG และ FGE เป็นมุมภายในและมุมภายนอกบนเส้นตัด GI กับเส้นขนาน FG และ HI จะได้ว่า HIG = FGE = 45o
จะเห็นว่าการรวมมุม FGE, FGH และ HGI เป็นมุมนั้นคือ มุม FGE + มุม FGH + มุม HGI = 180o
45o + x + 55o = 180o
จะได้ x = 80o นั้นคือ x / 2 = 40o
แหล่งที่มา
กระทรวงศึกษาธิการ. (2551). หนังสือสาระการเรียนรู้พื้นฐานคณิตศาสตร์ เล่ม 2 ชั้น มัธยมศึกษาปีที่ 2 (พิมพ์ครั้งที่ 1). กรุงเทพมหานคร.
กลับไปที่เนื้อหา
วงกลม
วงกลมเป็นรูปเรขาคณิตสองมิติชนิดหนึ่งที่พบได้ในธรรมชาติซึ่งเส้นโค้งของวงกลมจะห่างจากจุดที่ถูกตรึงไว้ (จุดศูนย์กลาง) เป็นระยะคงที่ และเรียกระยะห่างนี้ว่ารัศมี การวัดขนาดของวงกลมวัดได้จากเส้นผ่านศูนย์กลางเป็นเส้นตรงที่ยาวที่สุดที่เชื่อมระหว่างจุดสองจุดบนวงกลม ในบทเรียนนี้จะเป็นการศึกษาวงกลมในระบบเรขาคณิตยูคลิด ทฤษฎีทั้งหมดจะเกี่ยวข้องกับมุมและรูปสามเหลี่ยมที่แนบในวงกลม บทตั้งของบทเรียนจึงเป็นการวัดมุมที่เกิดจากการขยายด้านของรูปสามเหลี่ยม จากนั้นนำผลที่ได้ไปพิสูจน์ทฤษฎีสามบทได้แก่ 1) รูปสามเหลี่อมที่แนบในวงกลมซึ่งมีฐานเป็นเส้นผ่านศูนย์กลางและจุดยอดเป็นจุดบนเส้นรอบวงรูปสามเหลี่ยมนั้นจะเป็นรูปสามเหลี่ยมมุมฉาก 2) มุมที่จุดศูนย์ที่จะมีขนาดเป็นสองเท่าของมุมในส่วนโค้งของวงกลมที่รองรับส่วนโค้งเดียวกัน และ 3) มุมในส่วนโค้งที่รองรับส่วนโค้งเดียวกันจะมีขนาดเท่ากัน

ภาพปก บทเรียนเรื่องวงกลม
โดย วีระ ยุคุณธร
บทตั้ง 1 มุม ABC + มุม BAC = มุม ACD
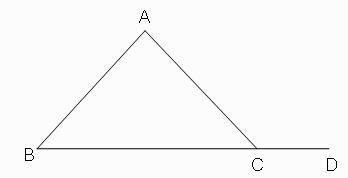
ภาพที่ 1 การต่อส่วนของเส้น CD จากด้าน BC ของรูปสามเหลี่อม
โดย วีระ ยุคุณธร
พิสูจน์ด้วยพีชคณิต
|
ข้อสรุป |
เหตุผล |
|
1. มุม ABC + มุม BAC + มุม ACB = 180o |
มุมภายในของรูปสามเหลี่ยม |
|
2. มุม ACB + มุม ACD = 180o |
มุมตรง |
|
3. มุม ABC + มุม BAC + มุม ACB = มุม ACB + มุม ACD |
สมบัติการเท่ากัน |
|
4. มุม ABC + มุม BAC = มุม ACD |
สมบัติการเท่ากัน |
พิสูจน์ด้วยเรขาคณิต
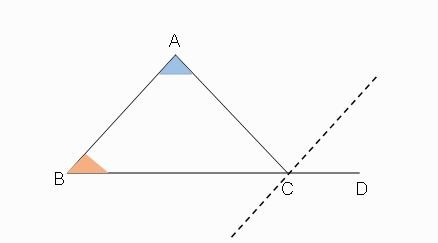
ภาพที่ 2 สร้างเส้นขนานกับด้าน AB โดยผ่านจุด C
โดย วีระ ยุคุณธร
เราสร้างส่วนของเส้นตรงผ่านจุด C ที่ซึ่งขนานกับส่วนของเส้นตรง AB จากการเท่ากันของมุมแย้งภายใน และ การเท่ากันของมุมภายในและมุมภายนอกบนด้านเดียวกันของเส้นตัดจะได้ว่า มุม ACD = มุม BAC + มุม ABC แสดงได้ดังภาพที่ 3
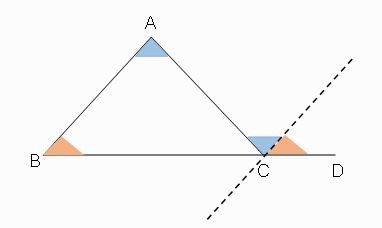
ภาพที่ 3 ผลการประยุกต์ใช้ทฤษฎีเส้นขนาน
โดย วีระ ยุคุณธร
ทฤษฎีบทที่ 1 รูปสามเหลี่อมแนบในวงกลมที่มีฐานเป็นเส้นผ่านศูนย์กลางและจุดยอดเป็นจุดบนเส้นรอบวงเป็นรูปสามเหลี่ยมมุมฉาก
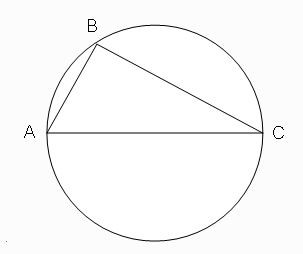
ภาพที่ 4 รูปสามเหลี่ยม ABC แนบในวงกลม
โดย วีระ ยุคุณธร
จะพิสูจน์ว่ารูปสามเหลี่ยม ABC เป็นสามเหลี่ยมมุมฉากนั้นคือ จะต้องแสดงว่า มุม B เป็นมุมฉาก
พิสูจน์ ลากเส้นจากจุดศูนย์กลางของวงกลมไปยังจุดยอดของสามเหลี่ยมจะเกิดรูปสามเหลี่ยมหน้าจั่วสองรูป (รูปสามเหลี่ยมที่ด้านสองด้านมีความยาวเท่ากับรัศมีของวงกลม) ผลของบทตั้งที่ 1 ทำให้เกิดภาพที่ 5
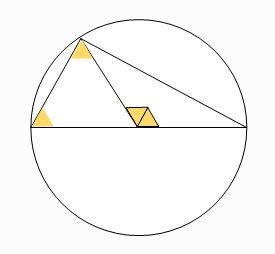
ภาพที่ 5 ผลการประยุกต์ใช้บทตั้ง
โดย วีระ ยุคุณธร
ในทำนองเดียวกันเมื่อพิจารณาสามเหลี่ยมที่เหลือจะได้
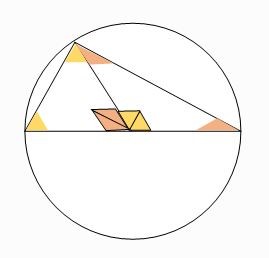
ภาพที่ 6 ผลการประยุกต์ใช้บทตั้งกับสามเหลี่ยมทั้งสองรูป
โดย วีระ ยุคุณธร
จะเห็นว่า ![]()
สรุปได้ว่ามุม B เป็นมุมฉากนั้นคือสามเหลี่อม ABC เป็นสามเหลี่ยมมุมฉากดังภาพที่ 7
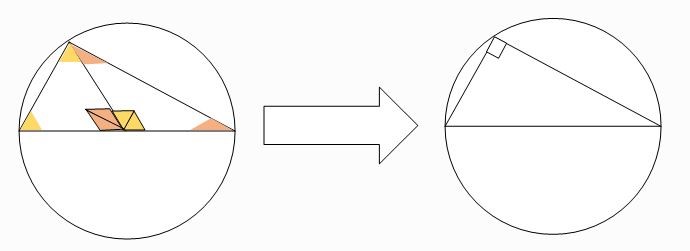
ภาพที่ 7 ภาพของทฤษฎีบทที่ 1
โดย วีระ ยุคุณธร
ทฤษฎีบทที่ 2 มุมที่จุดศูนย์ของวงกลมจะมีขนาดเป็นสองเท่าของมุมในส่วนโค้งของวงกลมที่รองรับส่วนโค้งเดียวกัน
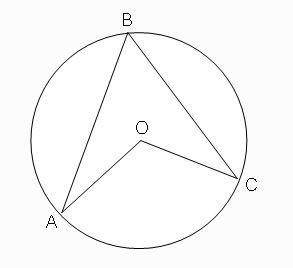
ภาพที่ 8 มุมที่จุดศูนย์กลางและมุมในส่วนโค้งของวงกลมที่รองรับส่วนโค้ง AC
โดย วีระ ยุคุณธร
จะพิสูจน์ว่า มุม AOC = 2 x มุม ABC
สร้างส่วนของเส้นตรงผ่านมุมในส่วนโค้งและมุมที่จุดศูนย์กลาง จากนั้นใช้บทตั้งที่ 1 จะได้ผลดังภาพที่ 9
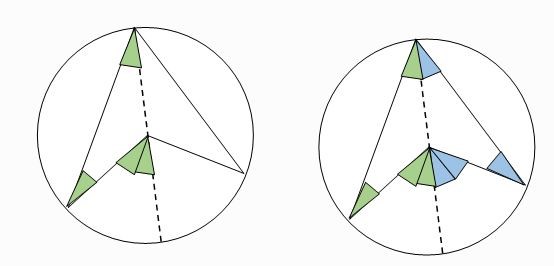
ภาพที่ 9 ผลการประยุกต์ใช้บทตั้งที่ 1 กับทฤษฎีบทที่ 2
โดย วีระ ยุคุณธร
จะเห็นได้ว่า
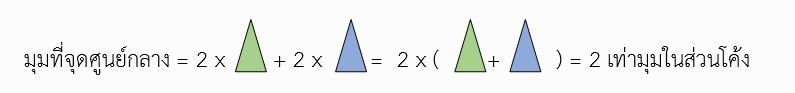
ดังนั้นมุมที่จุดศูนย์ของวงกลมจะมีขนาดเป็นสองเท่าของมุมในส่วนโค้งของวงกลมที่รองรับส่วนโค้งเดียวกัน
ทฤษฎีส่วนถัดไปเป็นทฤษฎีบทเล็กที่เห็นได้โดยง่ายจากทฤษฎีบทที่ 2 เป็นกรณีเฉพาะหรือข้อสังเกตที่พิสูจน์ได้ง่าย หากเราพิจารณามุมที่จุดศูนย์ซึ่งรองรับส่วนโค้ง AC หากเราย้ายจุดยอดไปไว้ที่ตำแหน่งมุมภายในส่วนโค้งเราจะพบว่ามุมเหล่านี้จะมีขนาดเท่ากันกล่าวคือเป็นครึ่งหนึ่งของมุมที่จุดศูนย์กลางเราเรียกทฤษฎีกลุ่มนี้ว่าบทแทรก
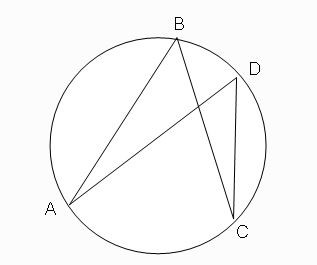
ภาพที่ 10 มุมภายในวงกลมที่รองรับส่วนโค้ง AC
โดย วีระ ยุคุณธร
บทแทรก 3 มุมในส่วนโค้งที่รองรับส่วนโค้งเดียวกันจะมีขนาดเท่ากัน
พิสูจน์ จะพิสูจน์ว่าในภาพที่ 10 มุม ABC = มุม ADC เราสร้างมุมที่จุดศูนย์กลางซึ่งรองรับส่วนโค้ง AC เมื่อประยุกต์ใช้ผลจากทฤษฎีบทที่ 2จะได้ดังภาพที่ 11 สรุปได้ว่า
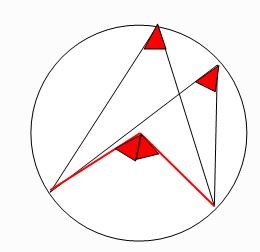
ภาพที่ 11 ผลการประยุกต์ใช้ทฤษฎีบทที่ 2
โดย วีระ ยุคุณธร
แหล่งที่มา
Surowski D.B. (2019, 20). Advanced High-School Mathemtics. Retrieved April 20, 2019, from http://search.saschina.org/surowski
กลับไปที่เนื้อหา
ความเท่ากันทุกประการ
การแปลงเรขาคณิตนั้นทำให้ได้รูปเรขาคณิตรูปใหม่ หากเราทำการแปลงเรขาคณิตด้วยการเลื่อนขนาด การสะท้อน หรือ การหมุน จะพบว่ารูปใหม่ที่ได้กับรูปต้นแบบมีรูปร่างเหมือนกันและมีขนาดเท่ากันเรียกการแปลงชนิดนี้ว่าเป็นการแปลงคงสภาพ แต่ถ้าเราทำการขยายหรือลดสเกลเราจะพบว่ารูปที่ได้กับรูปต้นแบบมีรูปร่างเหมือนกันแต่มีขนาดไม่เท่ากัน การแปลงเรขาคณิตข้างต้นดังที่กล่าวมานำมาซึ่งแนวคิดของความเท่ากันทุกประการและความคล้าย ในบทเรียนนี้เราจะศึกษาเรื่องความเท่ากันทุกประการโดยนิยามการเท่ากันทุกประการไว้ว่ารูปเรขาคณิตสองรูปจะเท่ากับทุกประการก็ต่อเมื่อรูปสองรูปนั้นทับกับได้สนิทซึ่งเราจะทำการศึกษาความเท่ากันทุกประการของรูปสามเหลี่ยมในเบื้องต้น

ภาพปกความเท่ากันทุกประการ
โดย วีระ ยุคุณธร
กิจกรรมที่ 1 สร้างความเข้าใจการเท่ากันทุกประการของรูปสามเหลี่ยมสองรูปแบบ ด้าน-มุม-ด้าน
กำหนดสามเหลี่ยมดังรูป
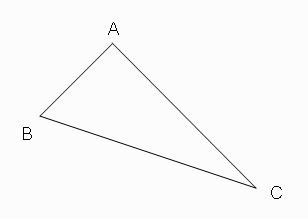
ภาพที่ 1 รูปสามเหลี่ยมต้นแบบ
โดย วีระ ยุคุณธร
จะสร้างรูปสามเหลี่ยม DEF ที่เท่ากันทุกประการกับสามเหลี่ยม ABC โดยมีคุณสมบัติสามข้อต่อไปนี้
- ด้าน DE = ด้าน AB
- มุม DEF = มุม ABC
- ด้าน EF = ด้าน BC
ขั้นตอนที่ 1 สร้างส่วนของเส้นตรง DE ให้มีขนานกับเท่า AB ดังภาพที่ 2
วิธีสร้าง กางวงเวียนรัศมี AB จากนั้นสร้างส่วนโค้งรอบจุด D จะได้เส้น DE ที่มีขนาดเท่ากับเส้น AB
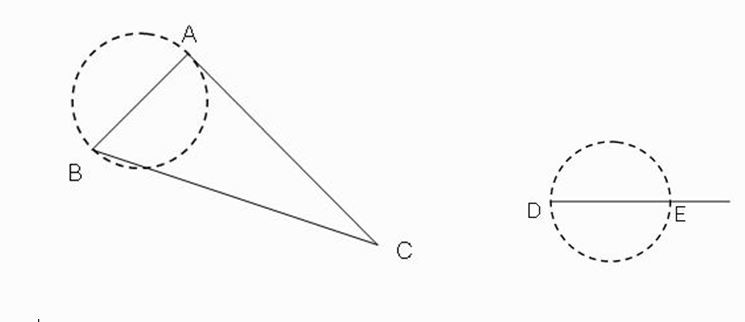
ภาพที่ 2 รูปที่ได้จากการสร้างในขั้นตอนที่ 1
โดย วีระ ยุคุณธร
ขั้นตอนที่ 2 สร้างมุม DEF ให้มีขนาดเท่ากับมุม ABC ดังภาพที่ 3
วิธีสร้าง สร้างส่วนโค้งสองส่วนโค้งดังนี้
ส่วนโค้งที่หนึ่ง: กางวงเวียนรอบจุด B จากนั้นสร้างส่วนโค้งให้ตัดด้าน AB และ BC จากนั้นใช้รัศมีเดียวกันสร้างส่วนโค้งรอบจุด E
ส่วนโค้งที่สอง: กางวงเวียนที่รัศมีเท่ากับระยะระหว่างจุดตัดของส่วนโค้งแรกกับด้าน AB และ BC จากนั้นนำไปสร้างส่วนโค้งที่สามรอบจุดตัดของส่วนโค้งที่สองกับด้าน DE
สร้างส่วนของเส้นตรงผ่านจุดตัดของส่วนโค้งทั้งสองจะได้มุมที่มีขนาดเท่ากับมุม ABC
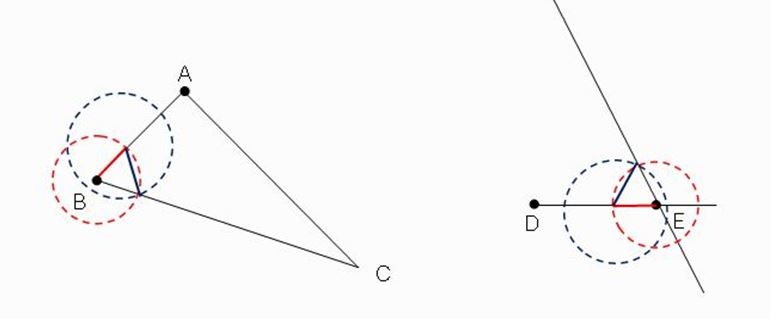
ภาพที่ 3 รูปที่ได้จากการสร้างในขั้นตอนที่ 2
โดย วีระ ยุคุณธร
ขั้นตอนที่ 3 สร้างส่วนของเส้นตรง EF ให้มีขนาดเท่ากับส่วนของเส้นตรง BC ดังภาพที่ 4
วิธีสร้าง กางวงเวียนรัศมี BC จากนั้นสร้างส่วนโค้งรอบจุด E โดยจุดตัดที่เกิดขึ้นคือจุด F ทำให้ได้ส่วนของเส้นตรง EF ซึ่งมีขนาดเท่ากับด้าน BC
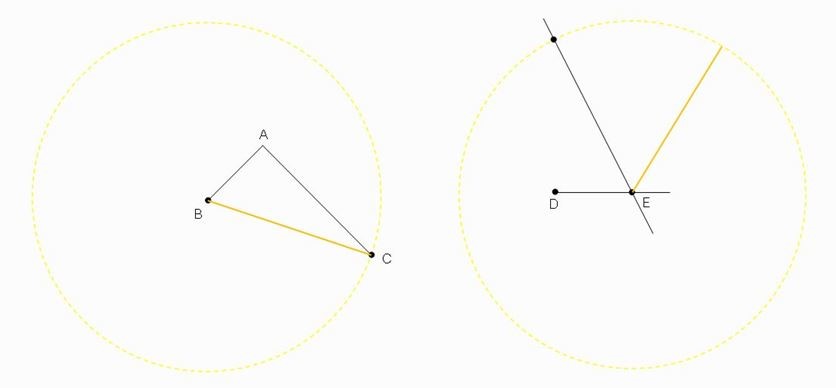
ภาพที่ 4 รูปที่ได้จากการสร้างในขั้นตอนที่ 3
โดย วีระ ยุคุณธร
ขั้นตอนที่ 4 ลากเส้นเชื่อมจุด F และ จุด D จะได้รูปปิดเป็นรูปสามเหลี่ยม DEF
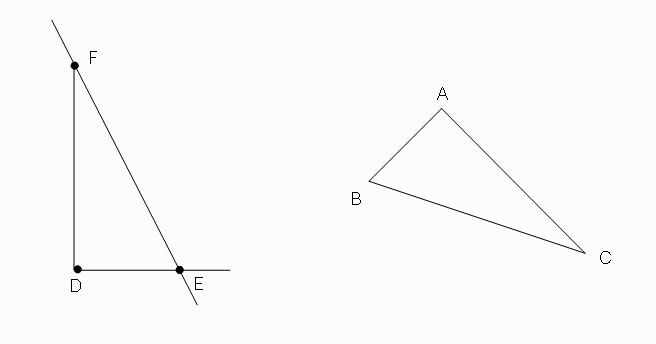
ภาพที่ 5 รูปที่ได้
โดย วีระ ยุคุณธร
เราสามารถตรวจสอบได้ว่ารูปสามเหลี่ยมสองรูปนี้เท่ากันทุกประการโดยอาศัยการแปลงทางเรขาคณิตทำให้เห็นว่ารูปสามเหลี่ยมของรูปนี้ทับกันสนิท
ข้อสรุป สามเหลี่ยมสองรูปที่มีด้านเท่ากันสองและมีมุมระหว่างด้านทั้งสองดังที่กล่าวมาข้างต้นมีขนาดเท่ากันแล้วสามเหลี่ยมสองรูปนี้เท่ากับทุกประการ
หมายเหตุ เราสามารถพิจารณาการเท่ากับทุกประการของรูปสามเหลี่ยมแบบ มุม-ด้าน-มุม, มุม-มุม-ด้าน, ด้าน-ด้าน-ด้าน และ ฉาก-ด้าน-ด้าน ได้ในทำนองเดียวกัน
กิจกรรมที่ 2 การวิเคราะห์และการพิสูจน์
จากข้อสอบ o-net ม.3 ปีการศึกษา 2560 กำหนดให้ P เป็นจุดกึ่งกลางของส่วนของเส้นตรง AB และ ส่วนของเส้นตรง CD โดยที่ขนาดของ AB ไม่เท่ากับ CD ดังรูป
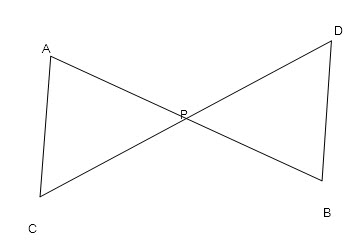
ภาพที่ 5 ภาพจากข้อสอบโอเน็ต ม.3 ปีการศึกษา 2560
โดย วีระ ยุคุณธร
สิ่งที่โจทย์กำหนดได้แก่
(D1) P เป็นจุดกึ่งกลางบนส่วนของเส้นตรง AB
(D2) P เป็นจุดกึ่งกลางบนส่วนของเส้นตรง CD
(D3) AB และ CD ยาวไม่เท่ากัน
2.1 วิเคราะห์ข้อค้นพบ
ข้อค้นพบจาก (D1) พบว่า AP = BP
ข้อค้นพบจาก (D2) พบว่า PC = PD
ข้อค้นพบจาก (D3) พบว่า AP และ PC ยาวไม่เท่ากันและ BP ยาวไม่เท่ากัน PD
2.2 ตั้งข้อสังเกตุและข้อคาดการณ์
ข้อสังเกตและข้อคาดการณ์ 1 รูปสามเหลี่ยม APC และ รูปสามเหลี่ยม PDB มีด้านยาวเท่ากันสองคู่ อาจเท่ากันทุกประการแบบ ด้าน-มุม-ด้าน หรือ ด้าน-ด้าน-ด้าน หรือ ฉาก-ด้าน-ด้าน
ข้อสังเกตและข้อคาดการณ์ 2 เนื่องจากมุม APC และ มุม DPB เป็นมุมตรงข้ามของเส้นตัดจะได้ว่ามุม APC และมุม DPB มีขนาดเท่านั้น ทำให้มั่นใจได้ว่า สามเหลี่ยม APC และ สามเหลี่ยม DPB เท่ากันทุกประการแบบด้าน- มุม-ด้าน
2.3 พิสูจน์ยืนยันข้อเท็จจริง
|
ข้อความ |
เหตุผล |
|
1. AP = BP |
P เป็นจุดกึ่งกลางของส่วนของเส้นตรง AB |
|
2. มุม APC = มุม BPD |
มุมตรงข้ามกันของเส้นตัด |
|
3. PC = PD |
P เป็นจุดกึ่งกลางของส่วนของเส้นตรง CD |
|
4. สามเหลี่ยม APC เท่ากับทุกประการกับ สามเหลี่ยม BPD แบบ ด้าน-มุม-ด้าน |
จาก 1,2 และ 3 |
กิจกรรมที่ 3 การวิเคราะห์และแก้ปัญหา
จากภาพที่ 4ข้อใดไม่ถูกต้อง
- สามเหลี่ยม ACP เท่ากันทุกประการกับสามเหลี่ยม BDP
- มุม CAP เท่ากับ มุม PDB
- ด้าน AC เท่ากับ ด้าน BD
- เส้น AC ขนานกับเส้น BD
วิธีทำ
จากการวิเคราะห์ข้างต้นเราพบว่า สามเหลี่ยม ACP เท่ากับทุกประการกับสามเหลี่ยม BDP ทำให้ได้ว่า ความยาวของด้านที่รองรับมุมคู่ที่เท่ากับจะมีขนาดเท่ากันในทางกลับกันคู่ของด้านที่เท่ากับจะมีมุมที่รองรับเท่ากับด้วยกล่าวคือ
(C1) มุม APC = มุม DPB ทำให้ได้ว่า AC = BD
(C2) ด้าน AP = ด้าน PB ทำให้ได้ว่า มุม ACP = มุม PDB
(C3) ด้าน CP = ด้าน PD ทำให้ได้ว่า มุม CAP = มุม PBD
(C4) จาก C2 และ C3 พบว่ามุมแย้งภายในบนเส้นตัดมีขนาดเท่ากันทำให้ได้ว่า เส้น AC ขนานกับเส้น BD
นำไปพิจารณาตัวเลือกพบว่า ข้อ 2 เป็นเท็จเพราะว่า มุม CAP และ มุม PDB มีด้าน CP และ PB รองรับแต่ขนาดของด้าน CP ไม่กันกับด้าน PB ส่งผลให้ มุมทั้งสองมีขนาดไม่เท่ากัน
แหล่งที่มา
กระทรวงศึกษาธิการ. (2551). หนังสือสาระการเรียนรู้พื้นฐานคณิตศาสตร์ เล่ม 1 ชั้น มัธยมศึกษาปีที่ 2 (พิมพ์ครั้งที่ 1). กรุงเทพมหานคร.
กลับไปที่เนื้อหา
ความคล้าย
การแปลงทางเรขาคณิตที่ทำให้เกิดภาพใหม่สอดคล้องคุณสมบัติสองประการคือมีรูปร่างแบบเดียวกันกับภาพต้นแบบแต่ขนาดของภาพอาจแตกต่างไปจากภาพต้นแบบ เรากล่าวไว้ว่าภาพที่ได้จากการแปลงและภาพต้นแบบเป็นภาพที่คล้ายกัน และเห็นได้ชัดเจนว่าภาพที่เท่ากันทุกประการกับภาพต้นแบบจะเป็นภาพที่คล้ายกันเสมอ ในบทเรียนนี้จะศึกษาเฉพาะรูปสามเหลี่ยมสองรูปที่คล้ายกัน
ภาพบทเรียนความคล้าย
โดยวีระ ยุคุณธร
นิยามความคล้ายของรูปสามเหลี่ยม
หลักการความคล้ายของรูปเรขาคณิตที่เราคุ้นเคยในชีวิตประจำวันคือการซูมบนหน้าจอคอมพิวเตอร์ หรือกล้องเราจะเห็นว่าภาพที่ได้จากการซูมนั้นรูปร่างยังคงเดิมแต่ขนาดเปลี่ยนไป สำหรับรูปทรงเรขาคณิตอย่างง่ายที่เราจะศึกษาคือรูปสามเหลี่ยมเนื่องจากเราสามารถแบ่งรูปหลายเหลี่ยมออกเป็นสามเหลี่ยมหลาย ๆ ได้รูปได้
ต่อไปเราจะเราพิจารณารูปสามเหลี่ยมที่คล้ายกันเมื่อเราทำการขยายขนาดรูปทางซ้ายมือขึ้นสองเท่าเราสังเกตว่า มุมของรูปสามเหลี่ยมสองรูปนี้จะเท่ากันแบบคู่ต่อคู่ อาจกล่าวได้ว่ามุมทั้งสามเป็นชุดเดียวกันนั้นคือ (40.8o, 66.2o, 73o)
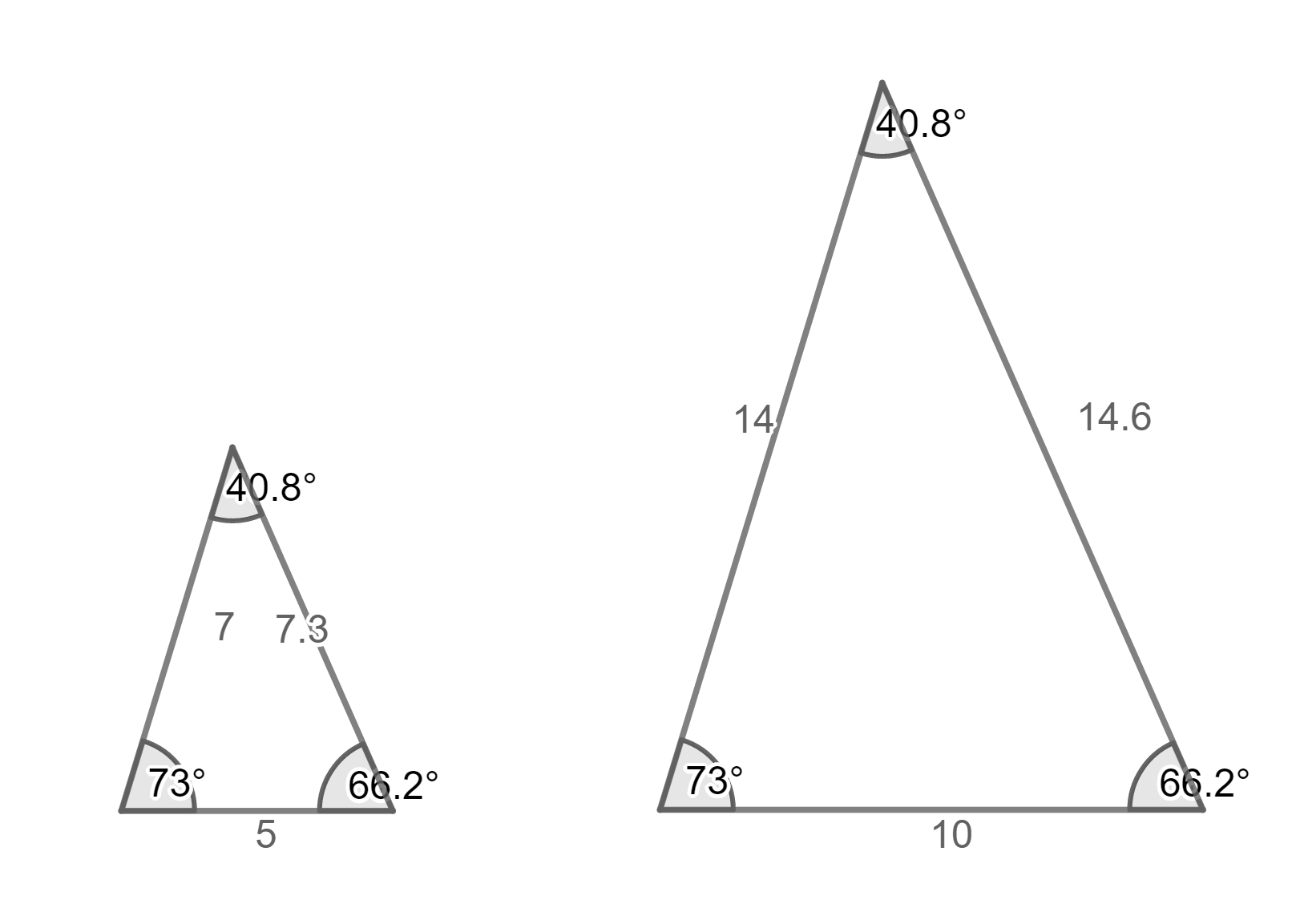
ภาพที่ 2 ภาพที่เกิดจากการแปลง(รูปขวา) มีขนาดให้เป็นสองเท่าของภาพต้นแบบ(รูปซ้าย)
โดย วีระ ยุคุณธร
จากข้อสังเกตในรูปที่ 2 เราจึงนิยามความคล้ายของรูปสามเหลี่ยมสองรูปไว้ดังนี้
นิยาม 1 ถ้ามุมทั้งสามมุมของรูปสามเหลี่ยมรูปหนึ่งเท่ากับมุมทั้งสามมุมของรูปสามเหลี่ยมอีกรูปหนึ่งแล้วเราจะกล่าวว่ารูปสามเหลี่ยมสองรูปนั้นคล้ายกัน
ข้อเท็จจริงในภาพที่ 3 เป็นรากฐานสำคัญการพิสูจน์และต่อยอดทฤษฏีมากมายอาทิทฤษฎีบทของเชวา (ceva’s theorem) ซึ่งไม่กล่าวถึงในบทเรียนนี้ ผลของภาพที่ 3 สามารถเรียบเรียงเป็นทฤษฎีบทต่อไปนี้
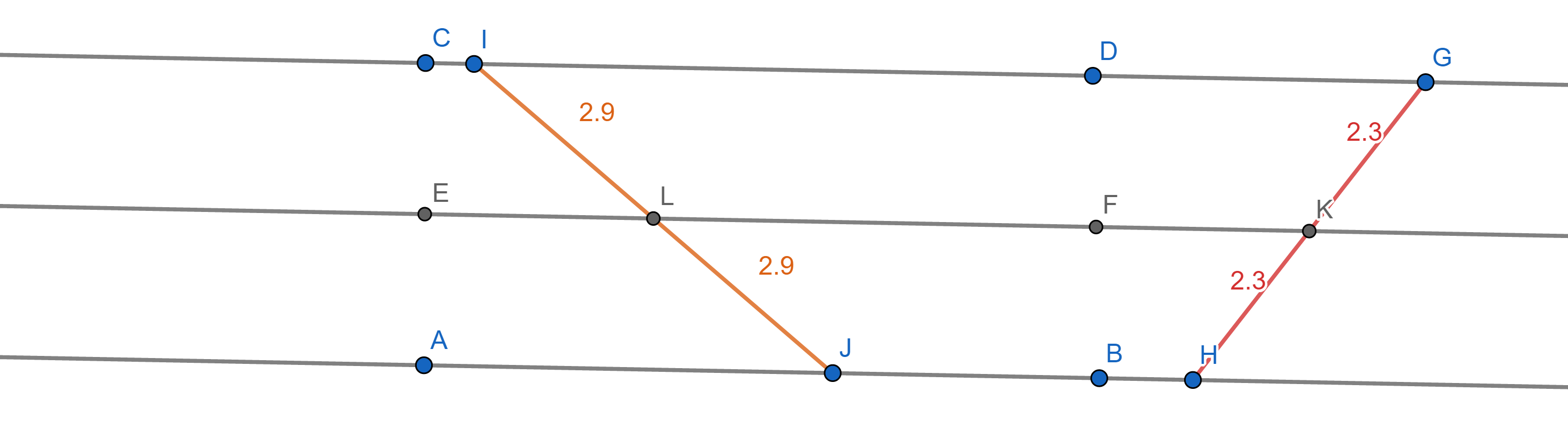
ภาพที่ 3 สัดส่วนของส่วนของเส้นตรงที่อยู่ภายในเส้นขนานสามเส้นเท่ากันทุกเส้น
โดย วีระ ยุคุณธร
ทฤษฎีบท 1 ถ้าเส้นขนานสามเส้นแบ่งครึ่งส่วนของเส้นตรงเส้นหนึ่งแล้วเส้นขนานสามเส้นนี้จะแบ่งครึ่งส่วนของเส้นตรงใด ๆที่เชื่อมต่อเส้นขนานขอบบนและขอบล่าง
พิสูจน์ พิจารณาภาพที่ 4
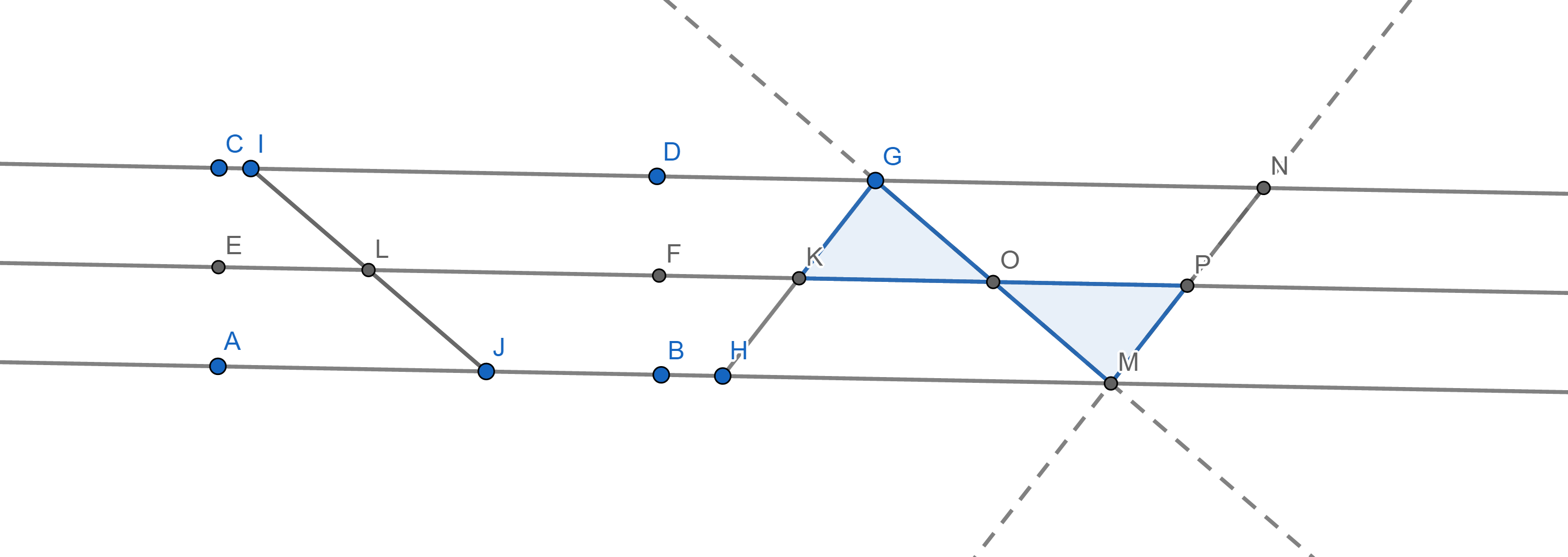
ภาพที่ 4 ภาพประกอบการพิสูจน์ทฤษฎีบท 1
โดย วีระ ยุคุณธร
|
ข้อความ |
เหตุผล |
|
1. GK=KH |
จากการสร้าง |
|
2. KH=PM |
คุณสมบัติสี่เหลี่ยมด้านขนาน KHMP |
|
3. GK=PM |
สมบัติการถ่ายทอดการเท่ากัน จาก 1 และ 2 |
|
4. มุม GKP = มุม KPM |
มุมแย้งภายในที่เกิดจากเส้น GM ตัดเส้นคู่ขนาน GH และ MN |
|
5. มุม KGM = มุม GMP |
มุมแย้งภายในที่เกิดจากเส้น GM ตัดเส้นคู่ขนาน GH และ MN |
|
6. สามเหลี่ยม GKO เท่ากันทุกประการกับ สามเหลี่ยม OPM แบบมุม-ด้าน-มุม |
จากข้อ 3-5 |
|
7. GO = OM |
จากข้อ 6 |
|
8. IL = LJ |
คุณสมบัติของสี่เหลี่ยมด้านขนาน ILOG และ LJMO |
การแบ่งเส้นออกเป็นสัดส่วน
ผลของทฤษฎีบทที่ 1 กล่าวถึงการแบ่งส่วนของเส้นตรงระหว่างเส้นขนานสามเส้นออกเป็นสองส่วนเท่ากัน ในขั้นตอนต่อไปเราจะขยายผลนี้ไปสู่อัตราส่วน s : t ใด ๆ โดยผ่านข้อตกลงของนิยามในภาพที่ 5
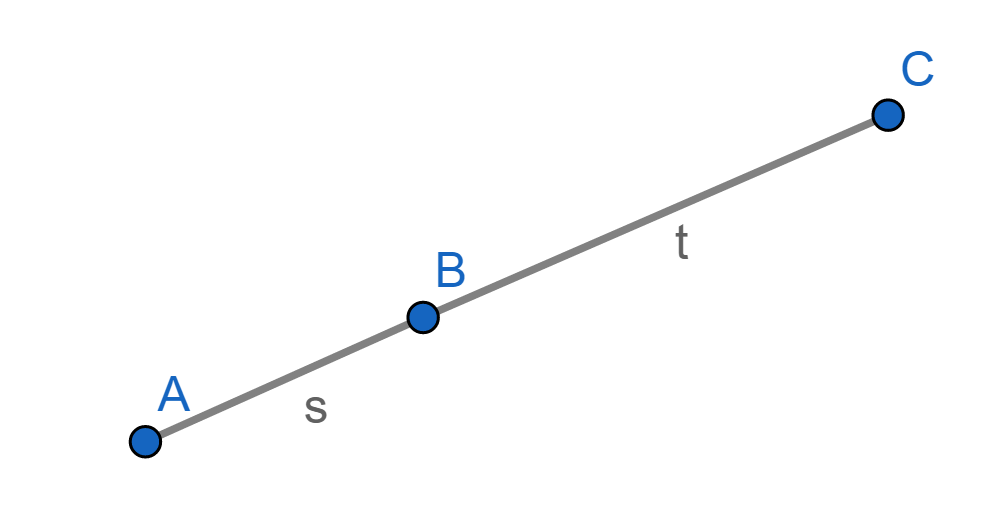
ภาพที่ 5 การแบ่งเส้นตรง AC เป็นอัตราส่วน s : t ด้วย จุด B
โดย วีระ ยุคุณธร
นิยาม 2 กำหนดให้ s และ t เป็นจำนวนจริงบวก เราจะกล่าวว่า จุด B แบ่งความยาวส่วนของเส้นตรง AC ด้วยอัตราส่วน s : t ถ้า
- B เป็นจุดบน AC
- ความยาวส่วนของเส้นตรง AB : ความยาวส่วนของเส้นตรง BC = s : t
เมื่อขยายผลทฤษฎีบท 1 แล้วเราจะได้ทฤษฎีบท 2
ทฤษฎีบท 2 สำหรับสามเหลี่ยม ABC ใด ๆ ถ้า เส้นตรง DE ขนาดกับด้าน BC และ ตัดด้าน AB ในอัตราส่วน s:t แล้ว เส้นตรงนี้จะตัดด้าน AC ด้วยอัตราส่วนเดียวกัน
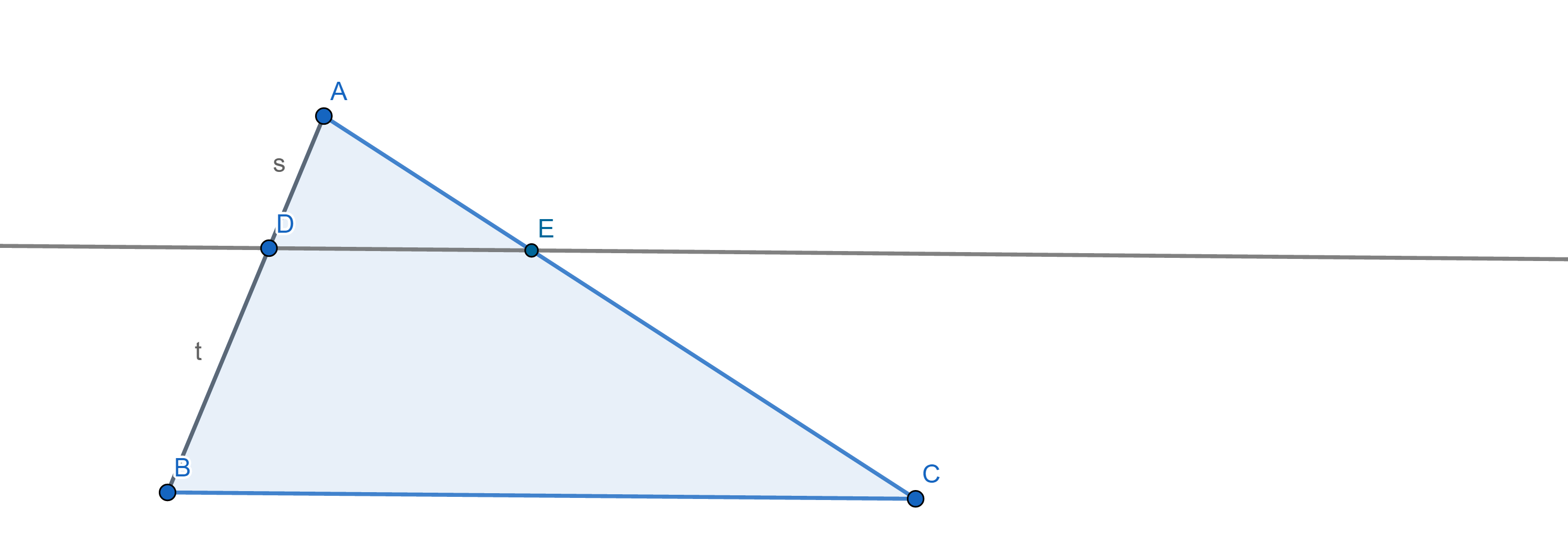
ภาพที่ 6 รูปการสร้างเส้นตรง DE โดยที่จุด D แบ่งส่วนของเส้นตรง AB ด้วยอัตราส่วน s : t
โดย วีระ ยุคุณธร
พิสูจน์ แบ่ง AB ออกเป็น s + t ส่วนด้วยเส้นขนานที่ระยะห่างแต่ละเส้นคงที่สม่ำเสมอโดย AD ถูกแบ่งออกเป็น s ส่วนเท่าๆกัน และ DB ถูกแบ่งออกเป็น t ส่วนเท่าๆกันตามลำดับดังภาพที่ 7
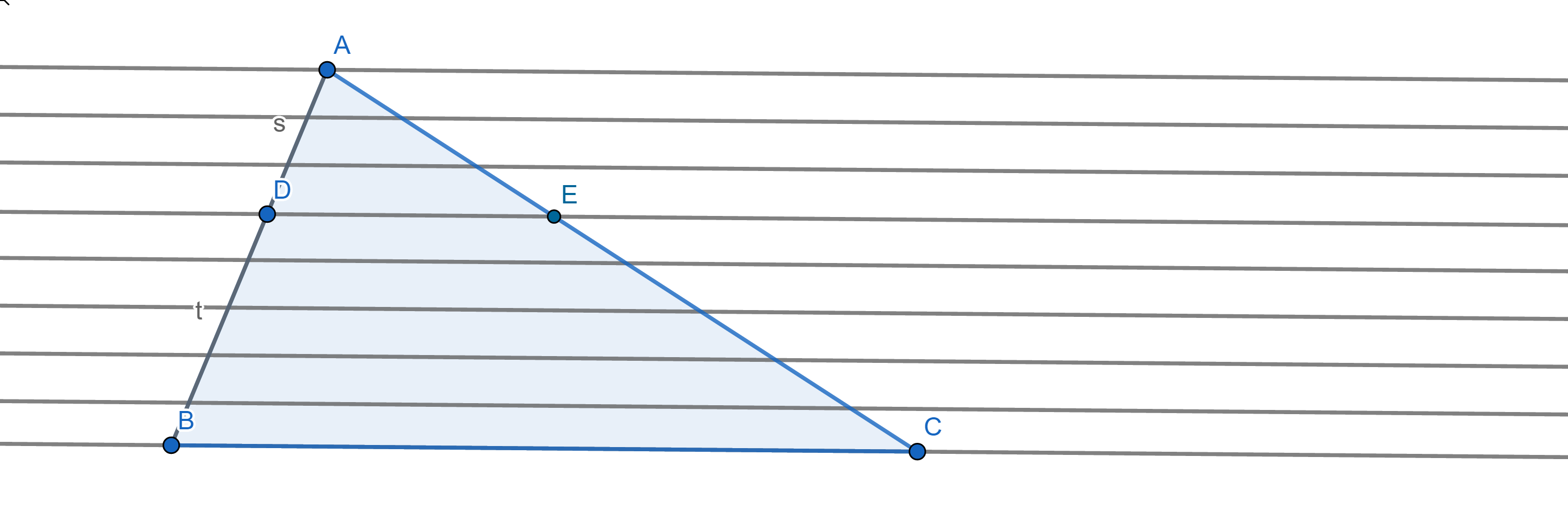
ภาพที่ 7 ส่วนของเส้นตรง AD และ DB ถูกแบ่งออกเป็น s และ t หน่วยตามลำดับ
โดย วีระ ยุคุณธร
พิจารณา 1 ส่วนของ AD และ AE จะพบว่ามีขนาด |AD| / s และ |DB| / t ตามลำดับ จากทฤษฎีก่อนหน้านี้ทำให้เราได้ว่า AE จะถูกแบ่งออกเป็น s ส่วนและ EC จะถูกแบ่งออกเป็น t
นั้นคือ |AE|/s = |EC|/t
นั้นคือ |AE| : |EC| = s : t
ทฤษฎีบทความคล้าย
เราตกลงกันตามนิยามการคล้ายกันของรูปสามเหลี่ยมสองรูปด้วยมุม ต่อมาเมื่อเราได้ทำการศึกษาคุณสมบัติของเส้นเราสามารถอธิบายความคล้ายของรูปสามเหลี่ยมสองรูปโดยการพิจารณาความยาวเส้นที่เป็นด้านของรูปสามเหลี่ยมได้ดังนี้
ทฤษฎีบท 3 ถ้าสามเหลี่ยมสองรูปมีมุมเท่ากับ 1 คู่ และอัตราส่วนแขนของมุมมีขนาดเท่ากันแล้วรูปสามเหลี่ยมสองรูปนี้คล้ายกัน
พิสูจน์ พิจารณาสามเหลี่ยมในภาพที่ 8 กำหนดให้ มุม DAE เท่ากับ มุม BAC และ |AD| / |AB| = |AE| / |AC| จะแสดงว่า สามเหลี่ยม ADE คล้ายกับ สามเหลี่ยม ABC พิจารณา
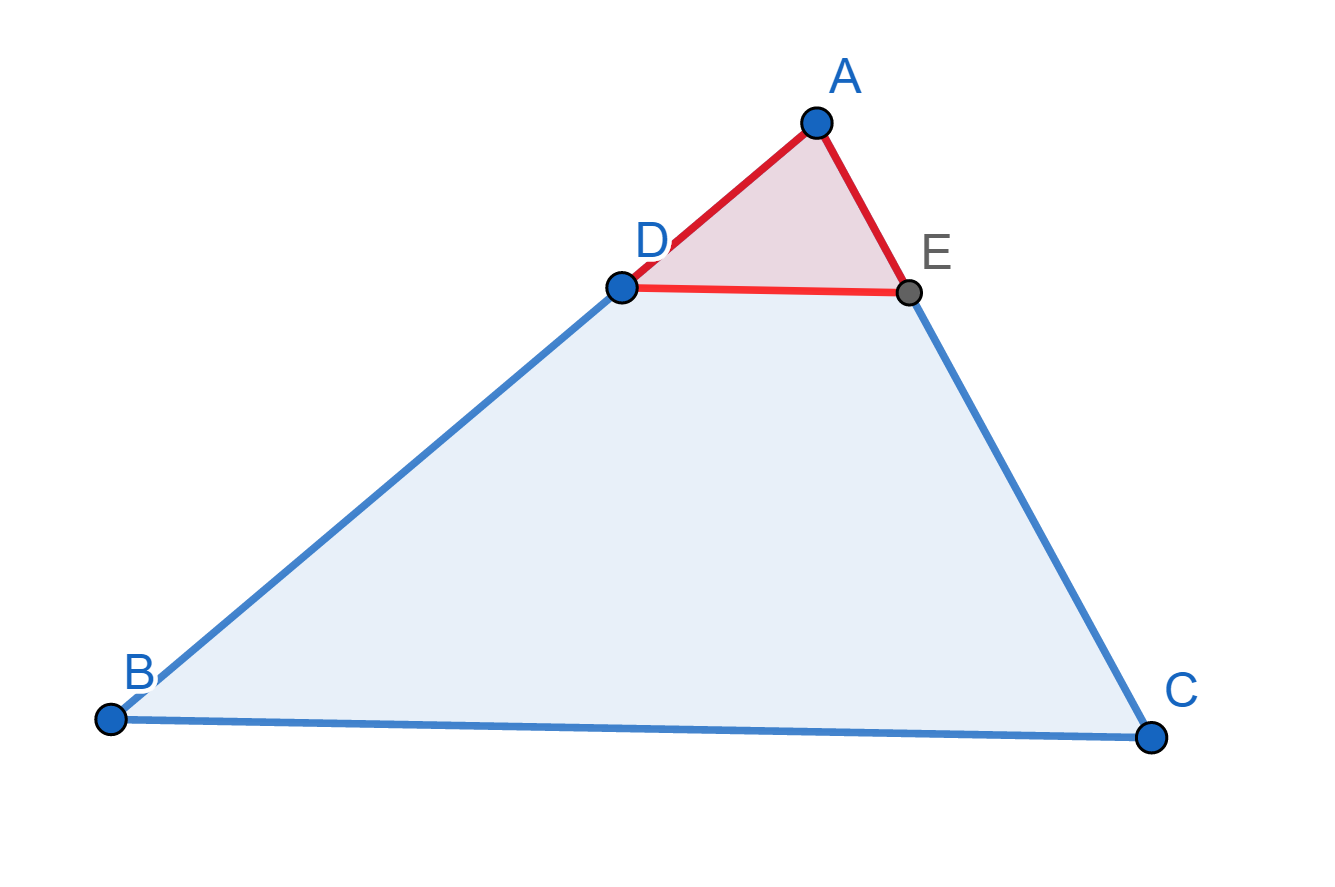
ภาพที่ 8 การซ้อนทับกันของมุมที่เท่ากันและแขนของมุมของรูปสามเหลี่ยมทั้งสองรูป
โดย วีระ ยุคุณธร
สร้างเส้น ตรงที่ขนานกับ BC ผ่านจุด D และตัดกับด้าน AC ที่จุด E’ ดังภาพที่ 9
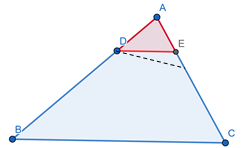
ภาพที่ 9 สร้างส่วนของเส้น DE’ ให้ขนานกัน BC
โดย วีระ ยุคุณธร
แน่นอนว่า สามเหลี่ยม ADE’ คล้ายกันกับสามเหลี่ยม ABC เนื่องจากมุมทั้งสามที่ขนาดเท่ากันทำให้ได้ว่า |AD| / |DB| = |AE’| / |AC|
เนื่องจากโจทย์กำหนดให้ |AD| / |AB| = |AE| / |AC| จะได้ว่า |AE’| / |AC| = |AE| / |AC| นั้นคือ |AE’| = |AE| ทำให้ได้ว่า E’ และ E เป็นจุดเดียวกัน นั้นคือ สามเหลี่ยม ADE และ สามเหลี่ยม ADE’ เท่ากันทุกประการทำให้ได้ว่า สามเหลี่ยม ADE คล้ายกันกับสามเหลี่ยม ABC
ทฤษฎีบท สามเหลี่ยมสองรูปจะคล้ายกัน แล้ว อัตราส่วนด้านที่สมนัยกันทั้งสามคู่มีขนาดเท่ากัน
พิสูจน์
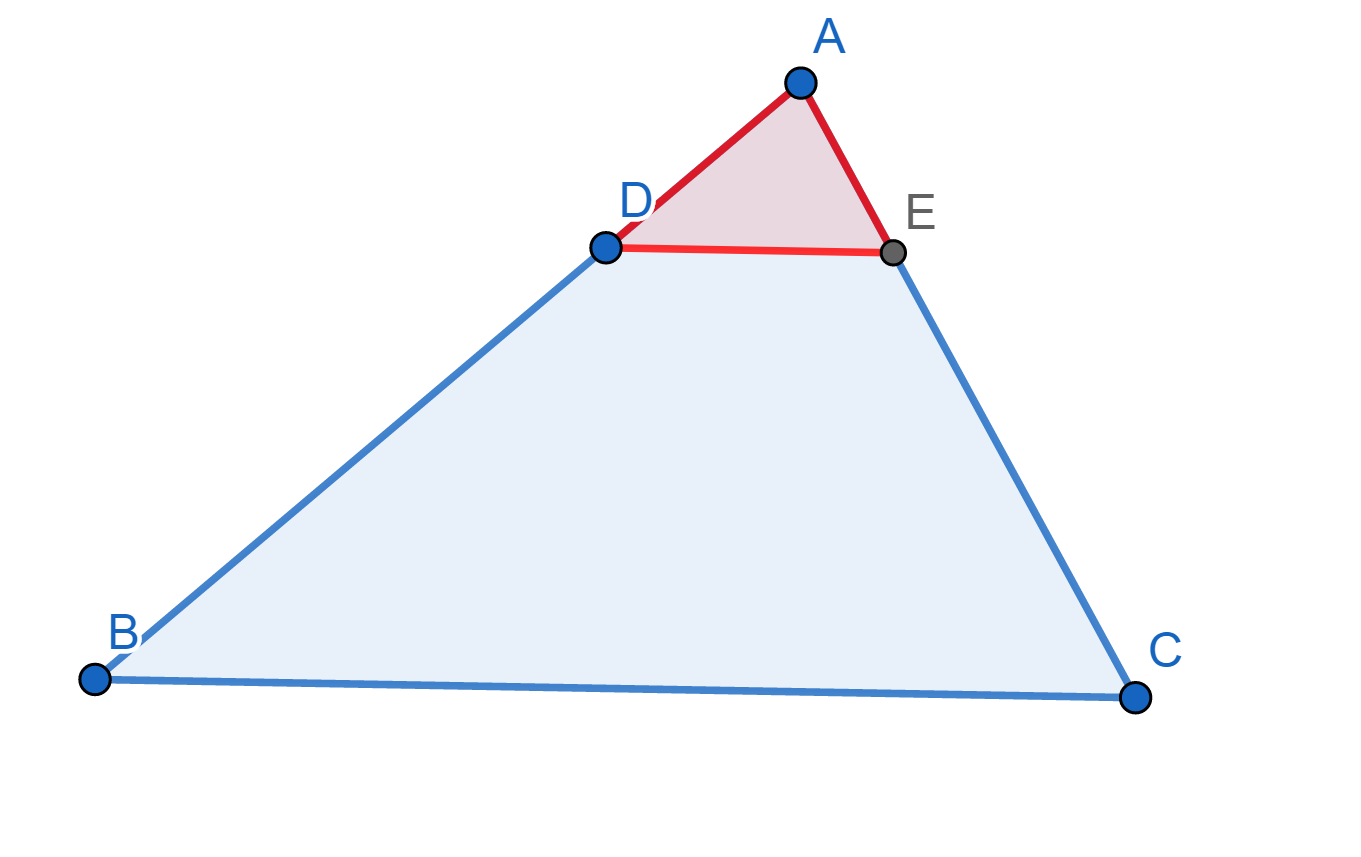
ภาพที่ 10 การสร้างรูปเพื่อเทียบสัดส่วนพื้นที่ไปสู่สัดส่วนความยาวฐานของรูปสามเหลี่ยมสองรูป
โดย วีระ ยุคุณธร
พิจารณา อัตราส่วน |AD| / |AB| สมมติให้ h เป็นความสูงของสามเหลี่ยม ADE ที่มี AD เป็นฐานจะได้ว่า h เป็นความสูงของสามเหลี่ยม AEB ด้วยจะเห็นว่า
|AD| : |AB| = 0.5h|AD| : 0.5h|AB| = พื้นที่สามเหลี่ยม ADE : พื้นที่สามเหลี่ยม AEB
ในทำนองเดียวกันถ้าให้ h’ เป็นความสูงของสามเหลี่ยม ADE ที่มี AE เป็นฐานแล้วจะได้ว่า
|AE| : |AC| = 0.5h|AE| : 0.5h|AC| = พื้นที่สามเหลี่ยม ADE : พื้นที่สามเหลี่ยม ADC
สังเกตว่า สามเหลี่ยม AEB และ สามเหลี่ยม ADC มีฐาน DE และความสูง ร่วมกัน จะได้ว่า
พื้นที่สามเหลี่ยม AEB = พื้นที่สามเหลี่ยม ADC
|AD| : |AB| = |AE| : |AC|
พิจารณาความสูงของสามเหลี่ยม ABC จากทฤษฎีการแบ่งสัดส่วนด้วยเส้นขนานถ้ากำหนดให้ h เป็นความสูงของ ADE และ H เป็นความสูงของ ABC แล้ว h : H = |AD| : |AB|
แหล่งที่มา
Patrick D. Barry. Geometry with Trigonometry. Horwood. Chichester. 2001. ISBN 1-898563-69-1.
Junior Cycle Course Committee, NCCA. Mathematics: Junior Certificate Guidelines for Teachers. Stationary Office, Dublin. 2002. ISBN 07557-1193-9.
Fiacre O’Cairbre, John McKeon, and Richard O. Watson. A Resource for Transition Year Mathematics Teachers. DES. Dublin. 2006.83
Anthony G. O’Farrell. School Geometry. IMTA Newsletter 109 (2009) 21-28.
กลับไปที่เนื้อหา
ทฤษฎีบทพิธากอรัส
ทฤษฎีบทพิธากอรัสเป็นทฤษฎีว่าด้วยรูปสามเหลี่ยมมุมฉากซึ่งเป็นรากฐานสำคัญของการใช้หลักเรขาคณิตในคณิตศาสตร์ อีกทั้งยังรวมไปถึงศาสตร์อย่างฟิสิกส์อีกด้วย เนื่องจากการเคลื่อนที่ในฟิสิกส์นั้นนิยมใช้ระบบพิกัดฉาก เมื่อพิจารณาการกระจัดจะพบว่าเรขาคณิตการเคลื่อนคือรูปสามเหลี่ยมมุมฉาก ดังนั้นทฤษฎีพิธากอรัสจึงเป็นที่รู้จักกันดี และการพิสูจน์ทฤษฎีบทพิธากอรัสนั้นมีได้หลากหลายวิธี มีนักคณิตศาสตร์หลายท่านที่พยายามที่จะพิสูจน์ทฤษฎีบทนี้ด้วยวิธีการที่แตกต่างกันไป

ทฤษฎีบทพิธากอรัส
โดย วีระ ยุคุณธร
ทฤษฎีบทพิธากอรัส
พิจารณาสามเหลี่ยมมุมฉาก BCA ในภาพที่ 2 มีด้าน CB และ CA เป็นด้านประกอบมุมฉากยาว 3 และ 4 หน่วยตามลำดับ ด้านตรงข้ามมุมฉาก BA มีขนาดเท่ากับ 5 หน่วย
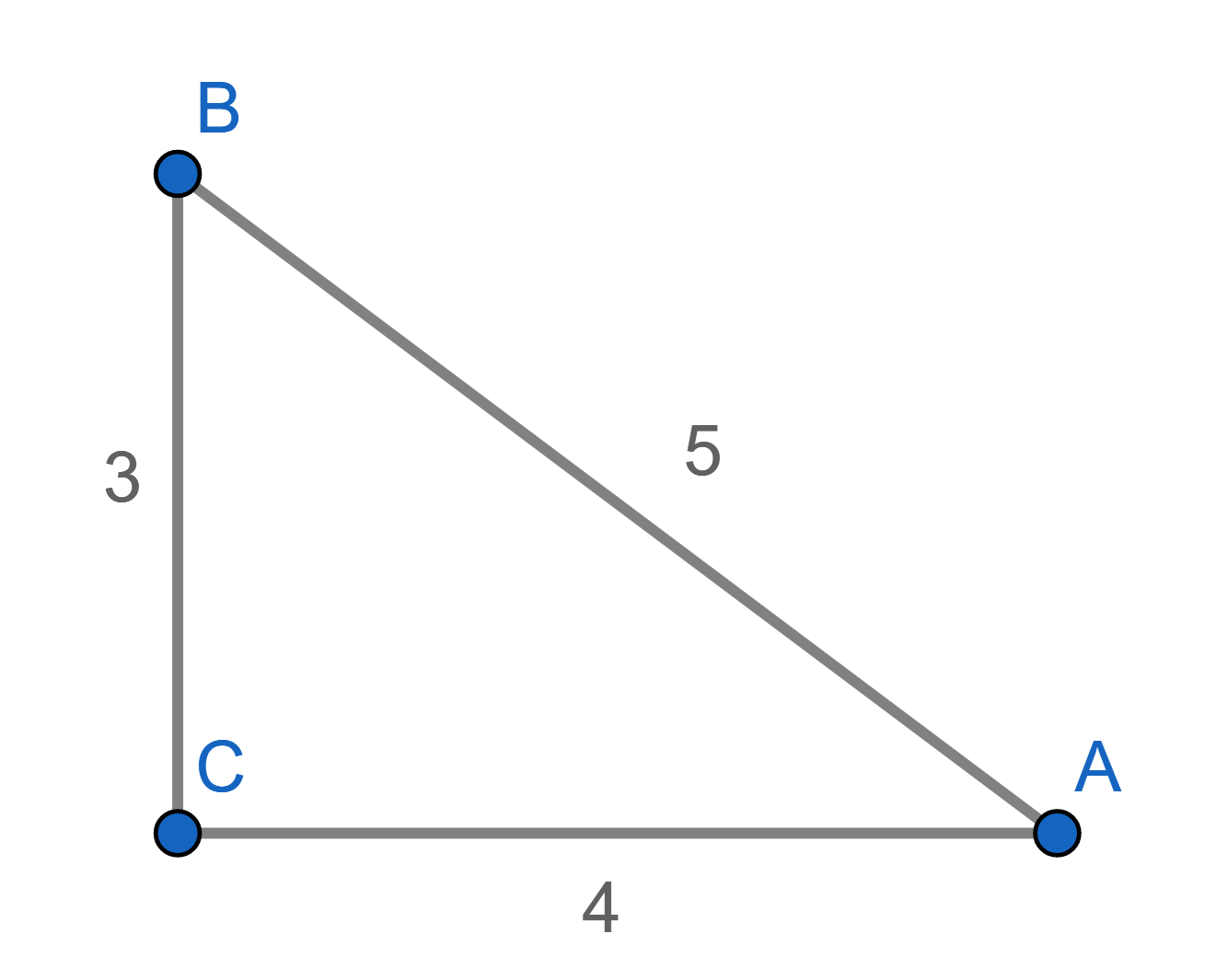
ภาพที่ 2 สามเหลี่ยมมุมฉาก BCA
โดยวีระ ยุคุณธร
พิจารณาพื้นที่สี่เหลี่ยมจัตุรัสบนด้านทั้งสามจะพบว่ามีขนาดพื้นที่ 9, 16, 25 ตารางหน่วยดังภาพที่ 3 สังเกตว่า 9 + 16 = 25 หรือ 32 + 42 = 52
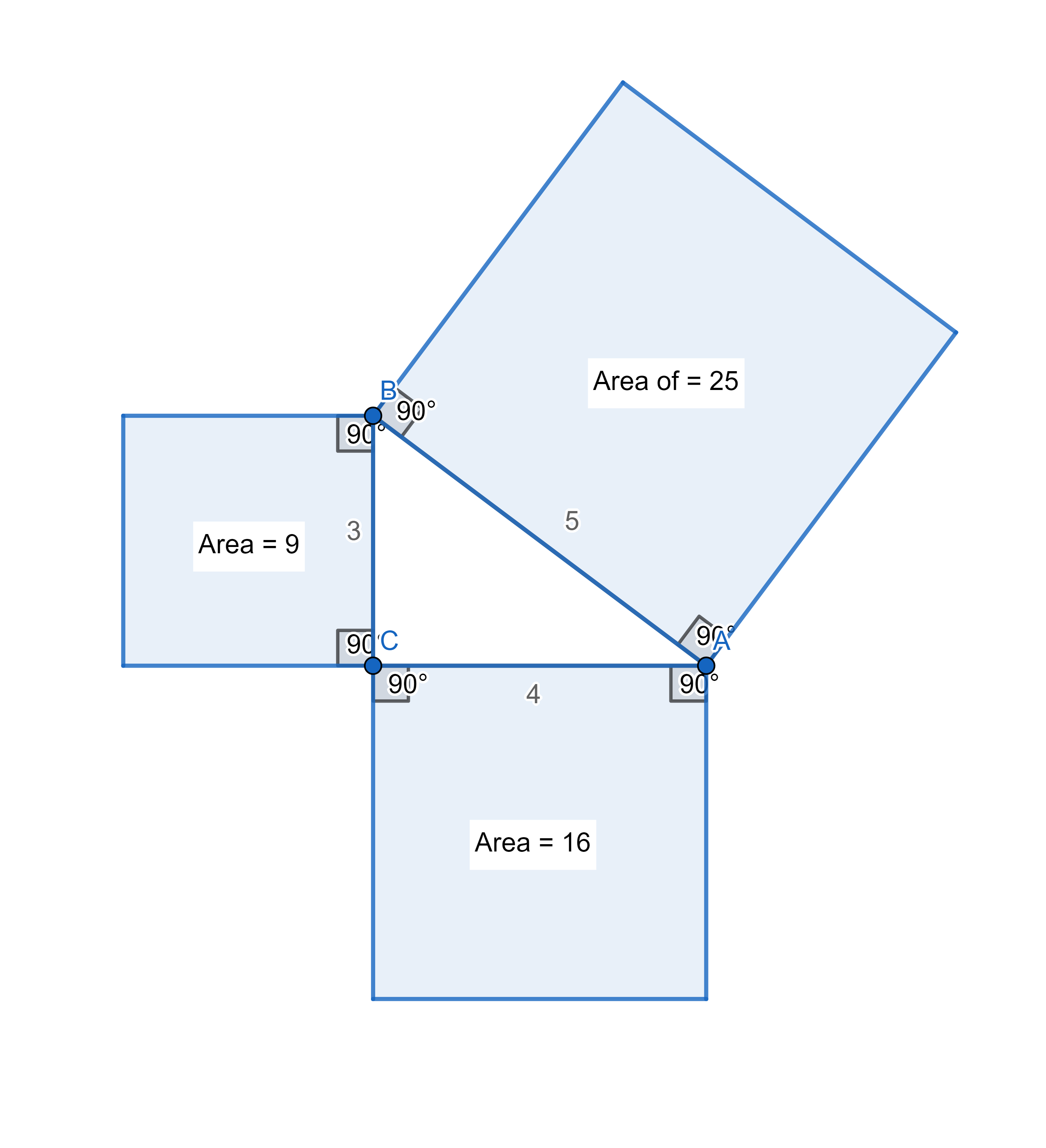
ภาพที่ 3 พื้นที่สี่เหลี่ยมจัตุรัสบนด้านทั้งสามของสามเหลี่ยมมุมฉาก BCA
โดยวีระ ยุคุณธร
เราอาจกล่าวได้ว่า “ผลรวมของพื้นที่สี่เหลี่ยมจัตุรัสบนด้านประกอบมุมฉากมีค่าเท่ากับพื้นที่ด้านตรงข้ามมุมฉาก”
ซึ่งทฤษฎีบทพิธากอรัสได้กล่าวไว้ว่า
- ถ้าสามเหลี่ยม BCA เป็นสามเหลี่ยมมุมฉากแล้ว BC2 + CA2 = AB2
- ถ้า BC2 + CA2 = AB2 แล้ว สามเหลี่ยม BCA เป็นสามเหลี่ยมมุมฉาก
นั้นคือ “ สามเหลี่ยม BCA เป็นสามเหลี่ยมมุมฉากก็ต่อเมื่อ BC2 + CA2 = AB2 “
เงื่อนไขการใช้ทฤษฎีบทพิธากอรัสคือเมื่อเรารู้ว่ารูปสามเหลี่ยมที่พิจารณาเป็นรูปสามเหลี่ยมมุมฉากและรู้ความยาวด้านสองด้านเราจะหาความยาวของด้านที่สามได้เสมอด้วยสูตร
กรณีหาความยาวด้านตรงข้ามมุมฉาก
AB = sqrt (BC2 + CA2)
กรณีหาความยาวด้านประกอบมุมฉาก
BC = sqrt (AB2 - CA2) และ CA = sqrt (AB2 - BC2)
ตัวอย่างที่ 1 สามเหลี่ยมมุมฉากรูปหนึ่งมีความยาวด้านประกอบมุมฉากยาว 8 และ 15 หน่วย จงหาความยาวด้านตรงข้ามมุมฉาก
วิธีทำ ความยาวด้านตรงข้ามมุมฉาก = sqrt (82 + 152) = sqrt (64 + 225) = sqrt (289) = 17 หน่วย
ตัวอย่างที่ 2 สามเหลี่ยมมุมฉากรูปหนึ่งมีความยาวด้านประกอบมุมฉากยาว 8 หน่วยและด้านตรงข้ามมุมฉากยาว 17 หน่วย จงหาความยาวด้านประกอบมุมฉากที่เหลือ
วิธีทำ ความยาวด้านประกอบมุมฉาก = sqrt (172 - 82) = sqrt (25x9) = 15 หน่วย
ในหัวข้อถัดไปจะศึกษาเกี่ยวกับบทพิสูจน์ทฤษฎีบทพิธากอรัส
บทพิสูจน์พิธากอรัสแบบที่ 1
นำรูปสามเหลี่ยมมุมฉาก 3, 4, 5 มาจัดเรียงให้เป็นรูปสี่เหลี่ยมจัตุรัสขนาด 7x7 ดังภาพที่ 4 พบว่าจะเกิดพื้นที่สี่เหลี่ยมจตุรัสขนาด 5x5 แนบในสี่เหลี่ยมขนาด 7x7 จะเห็นได้ว่า
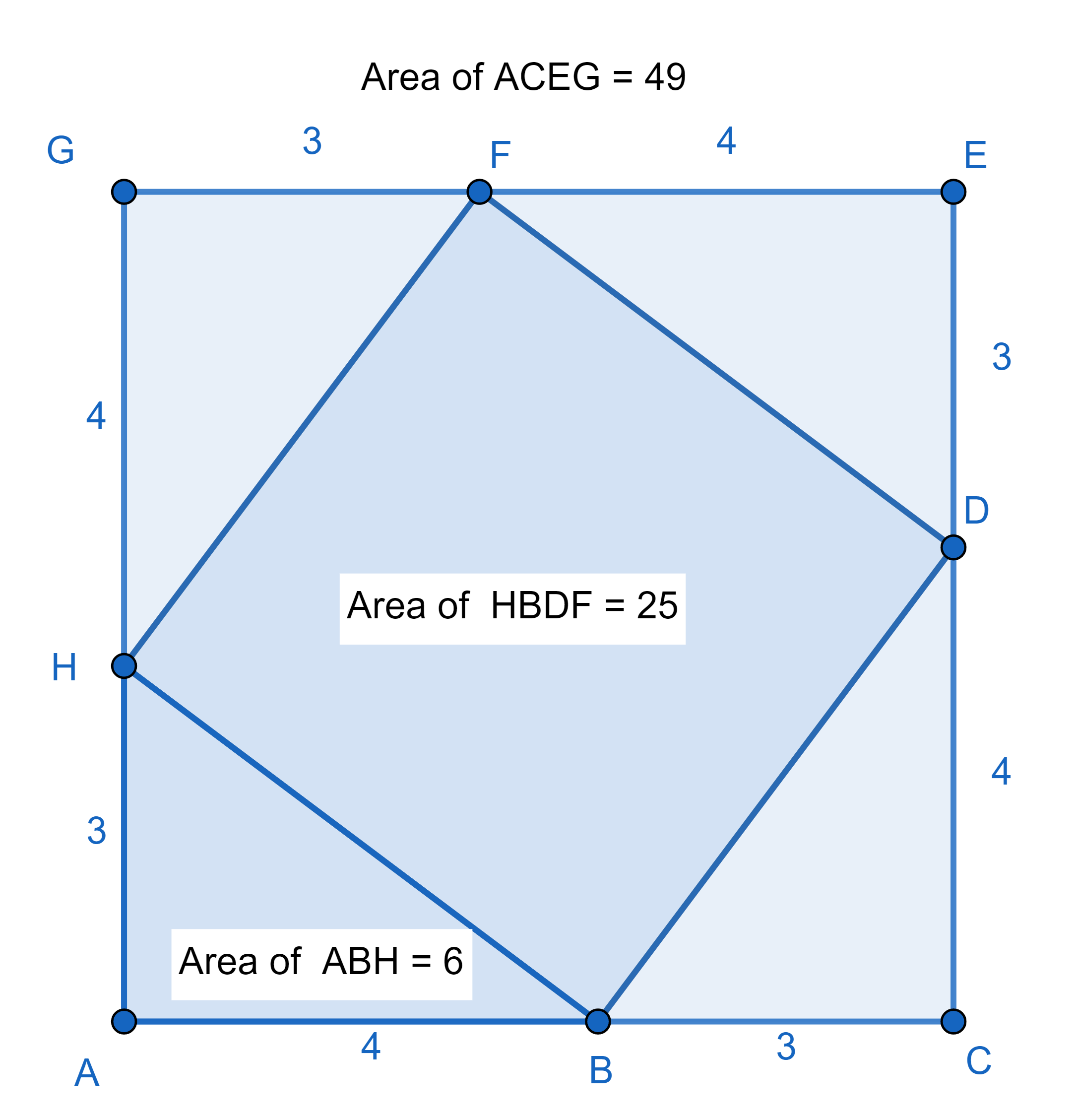
ภาพที่ 4 ภาพประกอบการพิสูจน์พิธากอรัสแบบที่ 1
โดยวีระ ยุคุณธร
พื้นที่สี่เหลี่ยมจัตุรัส 7x7 = พื้นที่สี่เหลี่ยมจัตุรัส 5x5 + 4(พื้นที่สามเหลี่ยม)
ถ้าเราทำการวางนัยยะทั่วไปให้ด้านของสามเหลี่ยมที่มีขนาด 3 เป็นตัวแปร a 4 เป็นตัวแปร b และ 5 เป็นตัวแปร c จะแสดงว่า a2 + b2 = c2 พิจารณา
พื้นที่สี่เหลี่ยมจัตุรัสรูปใหญ่ = พื้นที่สี่เหลี่ยมจัตุรัสรูปเล็ก + 4(พื้นที่สามเหลี่ยม)
(a + b)2 = c2 + 4(ab/2)
a2 + b2 + 2ab = c2 + 2ab
จะเห็นได้ว่า a2 + b2 = c2
บทพิสูจน์พิธากอรัสแบบที่ 2
จากรูปสามเหลี่ยมในภาพที่ 5 เป็นการนำสามเหลี่ยม 3, 4 , 5 หน่วยมาต่อกันโดยให้ด้านที่มีความยาว 4 หน่วยและความยาว 3 หน่วยเป็นฐาน จะทำให้เกิดรูปสี่เหลี่ยมคางหมูที่มีความสูง 7 มีด้านคู่ขนานยาว 3 และ 4 ตามลำดับ เมื่อพิจารณาพื้นที่สี่เหลี่ยมคางหมูดังกล่าวสามารถคำนวนได้จากการใช้พื้นที่สามเหลี่ยมสามรูป
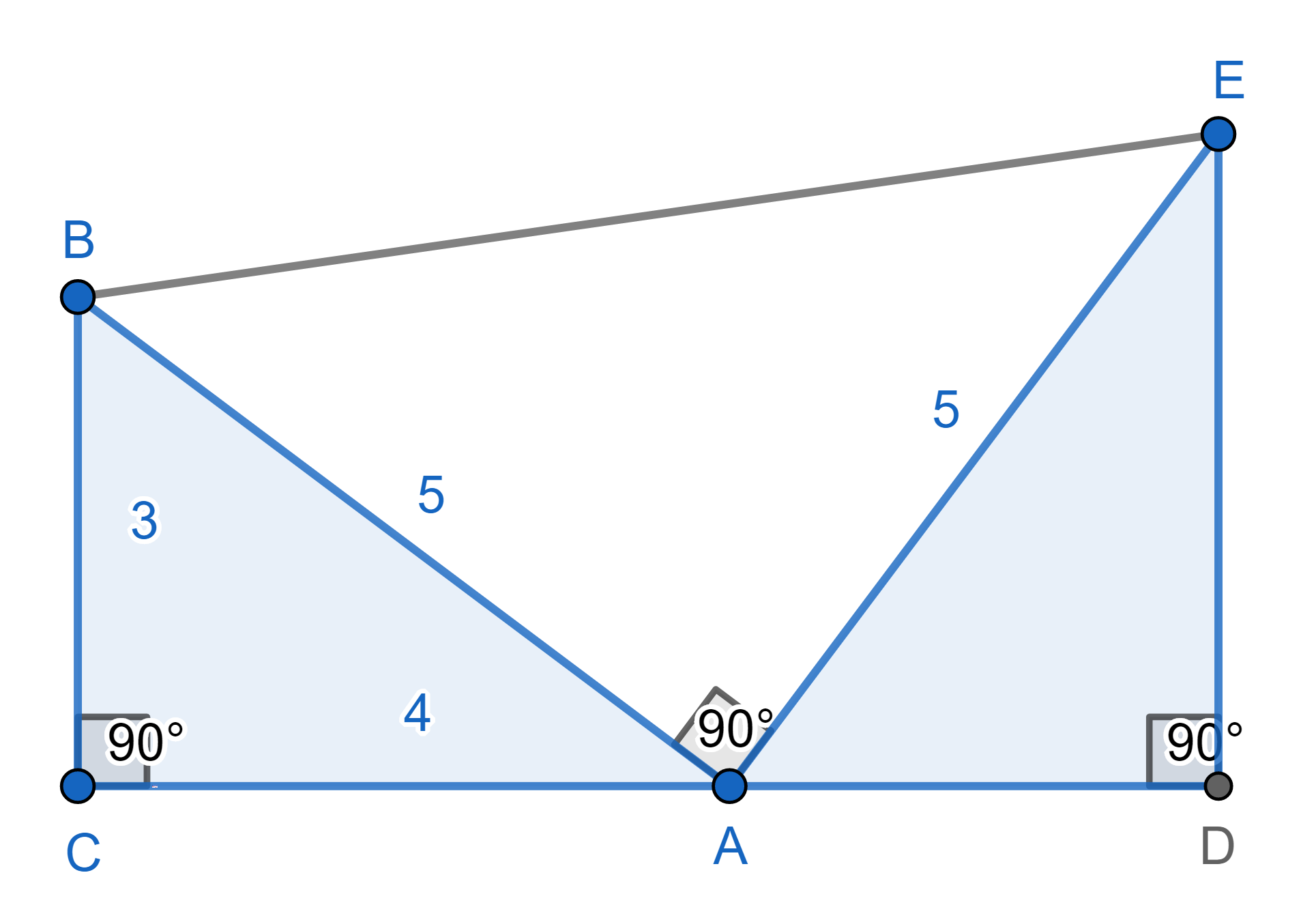
ภาพที่ 5 ภาพประกอบการพิสูจน์พิธากอรัสแบบที่ 2
โดยวีระ ยุคุณธร
พื้นที่สี่เหลี่ยมคางหมู = 1/2 x (ผลบวกด้านคู่ขนาน) x สูง = 1/2 x 7 x 7 = 24.5 และ ผลรวมพื้นที่สามเหลี่ยม = (3 x 4)/2 + (5 x 5)/2 + (3 x 4)/2 = 24.5 เมื่อพิจารณาการวางนัยยะทั่วไปในทำนองเดียวกันให้ด้านที่มีความยาว 3, 4, 5 หน่วยแทนด้วยตัวแปร a, b, c ตามลำดับ
พื้นที่สี่เหลี่ยมคางหมู = ผลรวมพื้นที่สามเหลี่ยม
1/2 x (a + b) x (a + b) = (ab/2) + (c2/2) + (ab/2)
(a + b)2 = c2 + 2ab
จะได้ว่า a2 + b2 = c2
ทฤษฎีบทของยูคลิดสำหรับส่วนของเส้นตรงแปรผัน
กำหนดรูปสามเหลี่ยมมุมฉากมีความยาวด้าน a, b และ c ตามลำดับ โดยที่ด้านตรงข้ามมุมฉาก c ถูกแบ่งด้วยเส้นตั้งฉากให้มีขนาด d และ e ตามลำดับในภาพที่ 6 เราจะแสดงว่า f2 = de, b2 = ce และ a2 = cd โดยการพิจารณาสมบัติความคล้ายของรูปสามเหลี่ยมสามรูปที่มีความยาวด้าน (d, f, a), (f, e, b) และ (a, b, c) จะได้อัตราส่วนด้านที่เท่ากันดังนี้
d/f = f/e = a/b และ d/a = f/b = a/c และ f/a = e/b = b/c
จะเห็นว่า
f2 = de และ a2 = cd และ b2 = ce
ในภาพที่ 7 แสดงตัวอย่างการคำนวณด้วยโปรแกรม GeoGebra โดยการสมมติตัวเลขแล้วแสดงผลการคำนวณเป็นไปตามกฏที่ค้นพบ
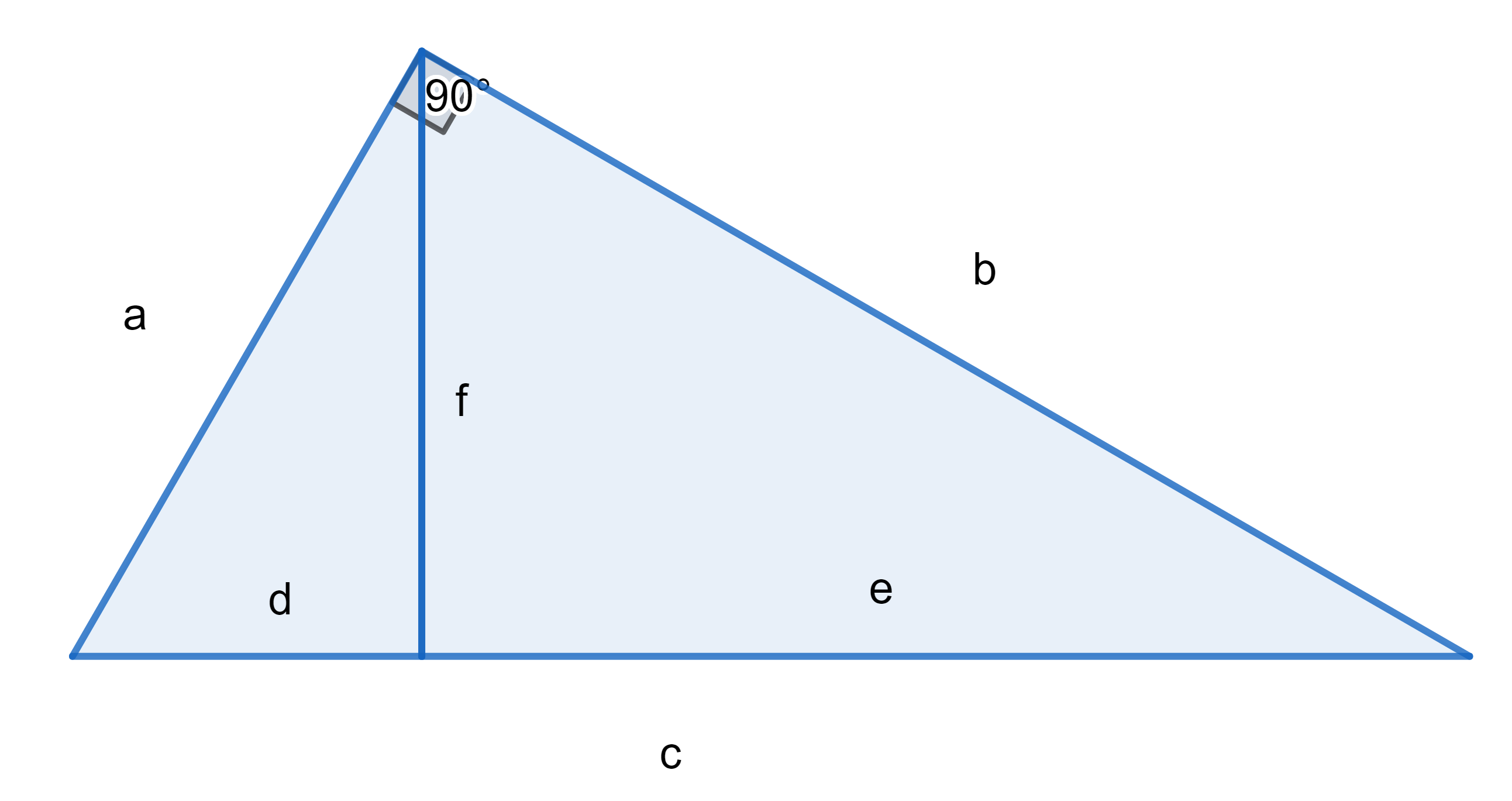
ภาพที่ 6 ภาพประกอบทฤษฎีบทของยูคลิดสำหรับส่วนของเส้นตรงแปรผัน
โดย วีระ ยุคุณธร
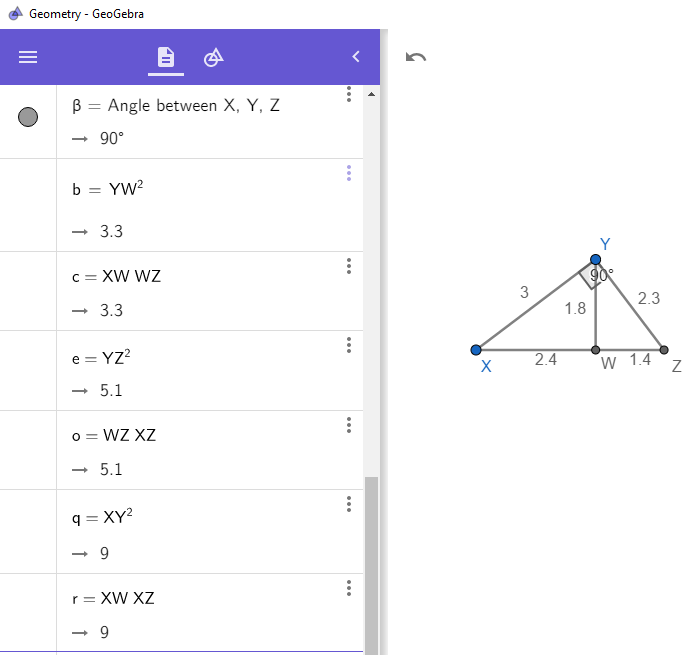
ภาพที่ 7 ภาพสาธิตการคำนวณส่วนของเส้นตรงแปรผัน
โดย วีระ ยุคุณธร
แหล่งที่มา
Patrick D. Barry. Geometry with Trigonometry. Horwood. Chichester. 2001. ISBN 1-898563-69-1.
Junior Cycle Course Committee, NCCA. Mathematics: Junior Certificate Guidelines for Teachers. Stationary Office, Dublin. 2002. ISBN 07557-1193-9.
Fiacre O’Cairbre, John McKeon, and Richard O. Watson. A Resource for Transition Year Mathematics Teachers. DES. Dublin. 2006.83
Anthony G. O’Farrell. School Geometry. IMTA Newsletter 109 (2009) 21-28.
กลับไปที่เนื้อหา
กฎของไซน์และโคไซน์
รูปสามเหลี่ยมมุมฉากสมมติให้มีความยาวด้านเป็น a, b, c ดังภาพที่ 1 เมื่อพิจารณาอัตราส่วนความยาวด้านมี 6 รูปแบบได้แก่ a/c, c/a, b/c, c/b, a/b และ b/a แทนอัตราส่วนตรีโกณมิติ sin A, cosec A, cos A, sec A, tan A และ cot A ตามลำดับ
ภาพปก กฎไซน์และโคไซน์
โดยวีระ ยุคุณธร
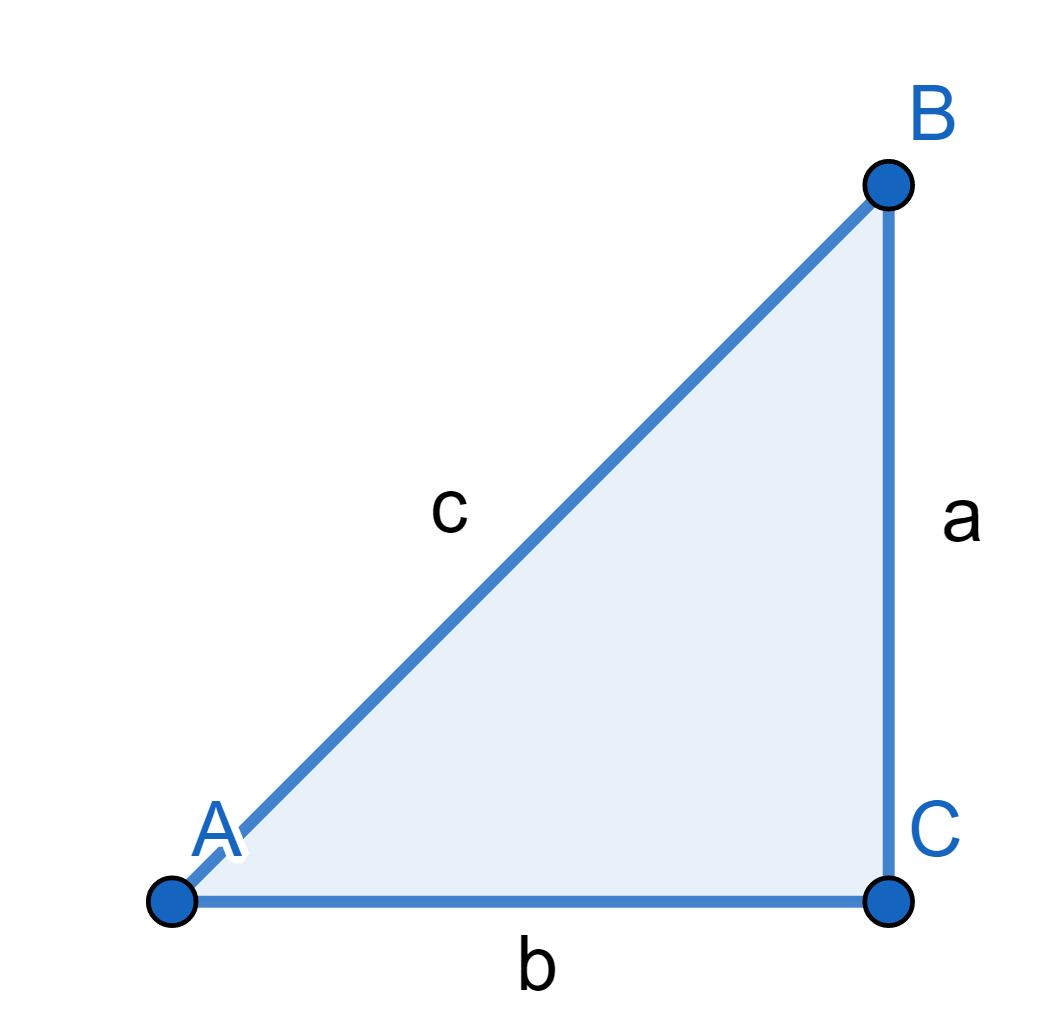
ภาพที่ 1 สามเหลี่ยมมุมฉาก BCA
โดยวีระ ยุคุณธร
แต่หากเราพิจารณารูปสามเหลี่ยมมุมฉากโดยกำหนดให้สามเหลี่ยมดังกล่าวมีความยาวด้านเป็น x, y และ r ตามแนวแกนพิกัดในวงกลมจะได้ว่า cos A = x/r = y/sqrt(x2 + y2) และ sin A = y/r = y/sqrt(x2 + y2)
วัดมุมจากจุด B หมุนในทิศทวนเข็มนาฬิกาไปยังจุด C ซึ่งอยู่ในคอวดรันด์ที่ 1 ( 0 องศา < มุม < 90 องศา) 0 < cos A และ 0 < sin A
วัดมุมจากจุด B หมุนในทิศทวนเข็มนาฬิกาไปยังจุด D ซึ่งอยู่ในคอวดรันด์ที่ 2 ( 90 องศา < มุม < 180 องศา) 0 > cos A และ 0 < sin A
วัดมุมจากจุด B หมุนในทิศทวนเข็มนาฬิกาไปยังจุด E ซึ่งอยู่ในคอวดรันด์ที่ 3 ( 180 องศา < มุม < 270 องศา) 0 > cos A และ 0 > sin A
วัดมุมจากจุด B หมุนในทิศทวนเข็มนาฬิกาไปยังจุด F ซึ่งอยู่ในคอวดรันด์ที่ 4 ( 270 องศา < มุม < 360 องศา) 0 < cos A และ 0 > sin A
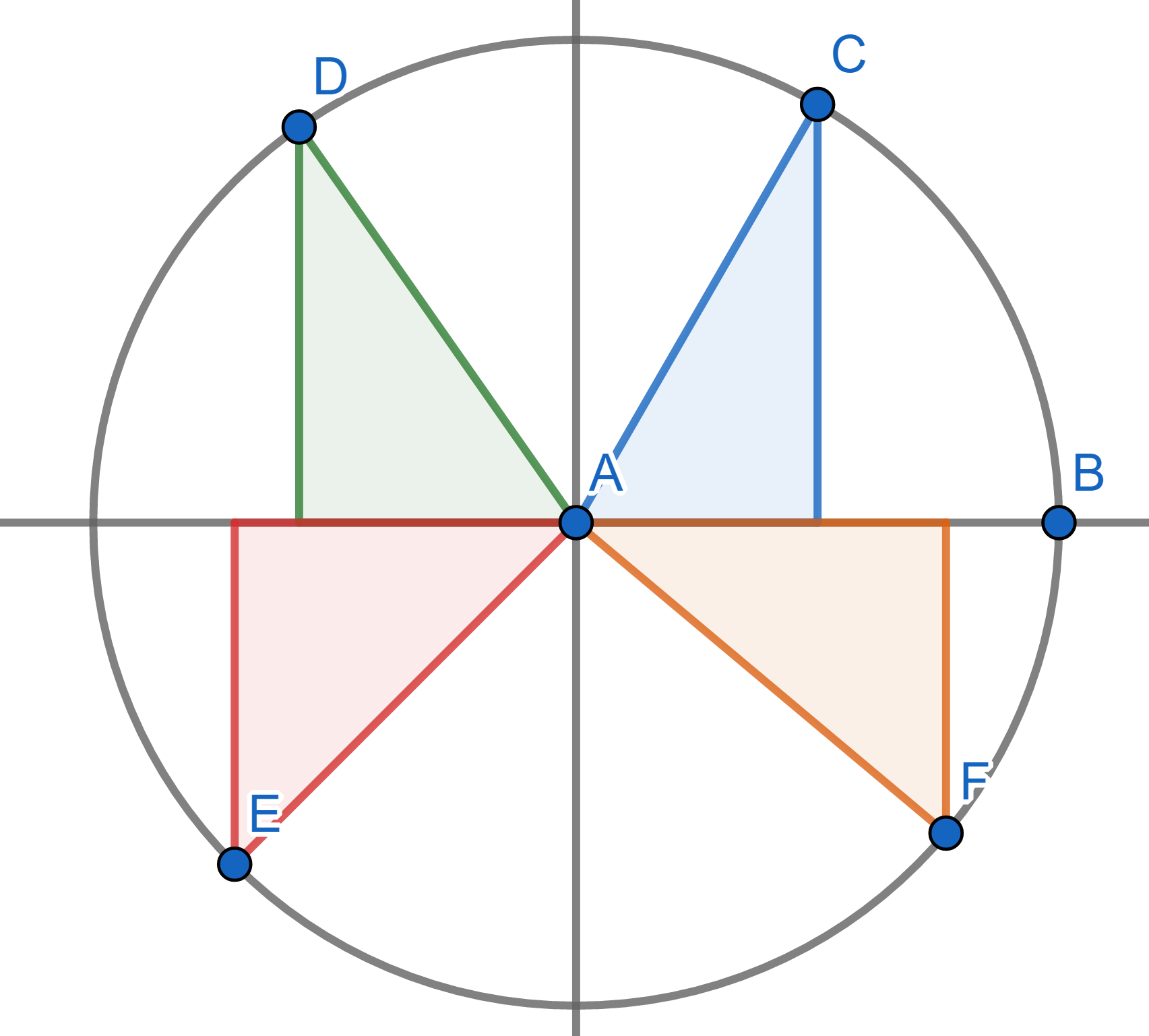
ภาพที่ 3 รูปสามเหลี่ยมมุมฉากในสี่ควอดรันด์
โดยวีระ ยุคุณธร
นอกจากนี้สังเกตได้ว่า sin(180-x) = sin(x) และ cos(180-x) = cos(x) พิจารณาทฤษฎีบทพิธากอรัสจะได้
r2 = x2 + y2
1 = (x/r)2 + (y/r)2
1 = sin2A + cos2A
เป็นเอกลักษณ์ตรีโกณมิติ
กฎของไซน์
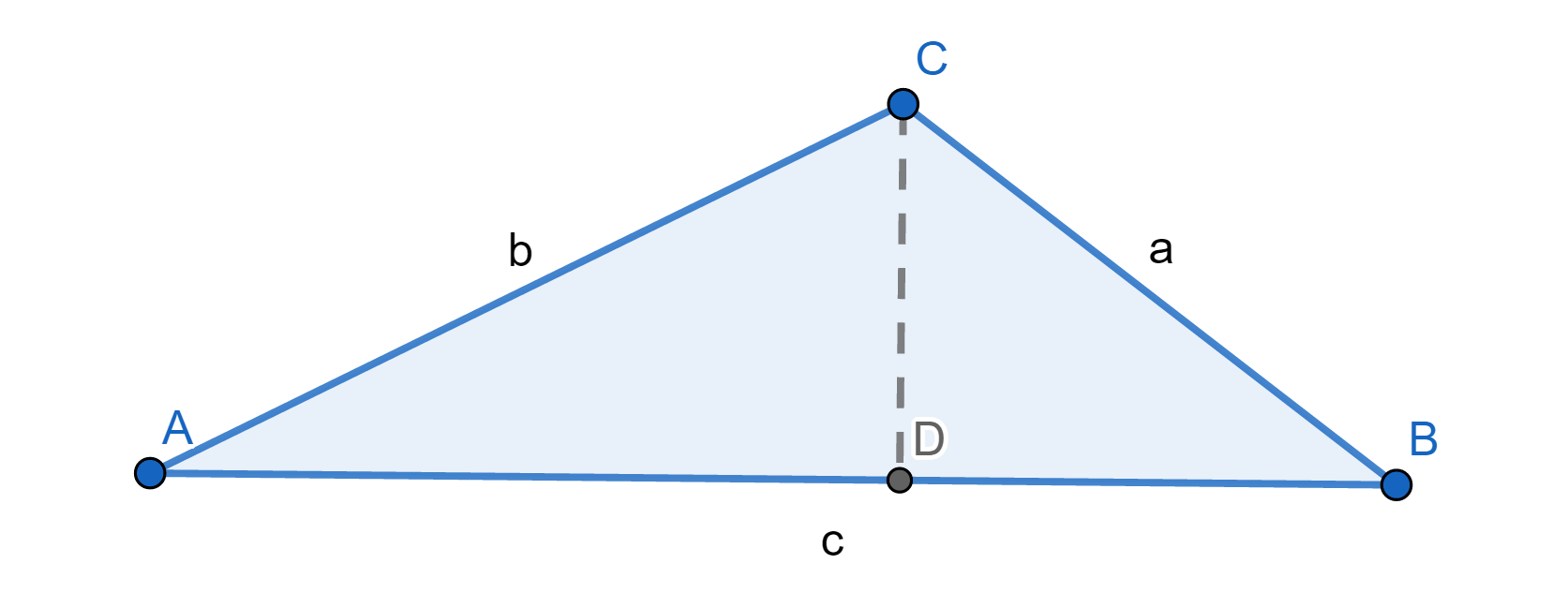
กำหนดรูปสามเหลี่ยมใด ๆ มีความยาวด้านตรงข้ามมุม A, B และ C มีขนาด a, b และ c หน่วยตามลำดับดังภาพที่ 4
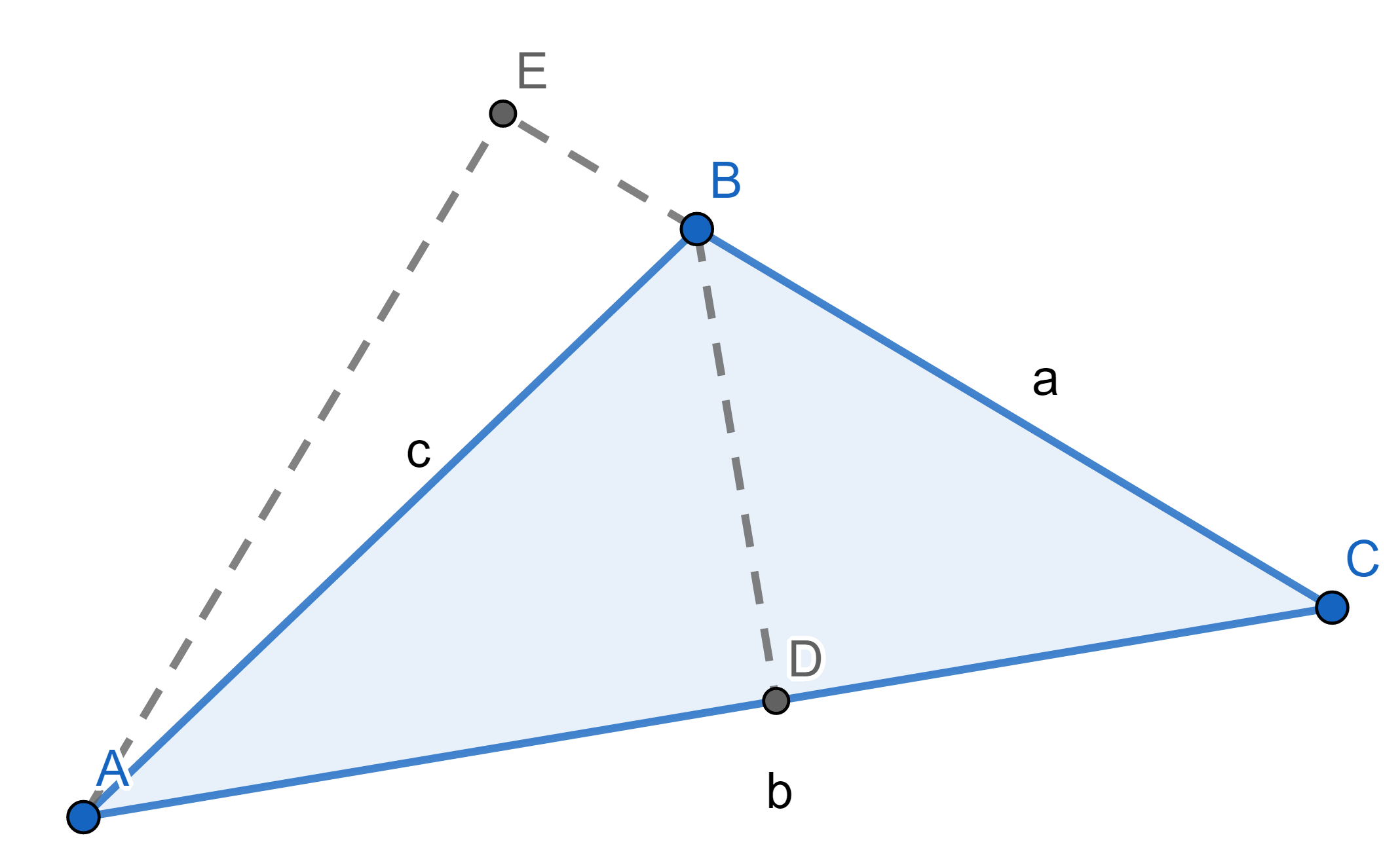
ภาพที่ 4 รูปสามเหลี่ยมประกอบการพิสูจน์กฎของไซน์
โดยวีระ ยุคุณธร
พิจารณาพื้นที่สามเหลี่ยม ABC โดยใช้ b เป็นฐานและ BD เป็นความสูงมีค่าเท่ากับ a sin C และ c sin A จะได้ว่า (b x a sin C) / 2 = (b x c sin A) /2
ดังนั้น sin A / a = sin C / c
ในทำนองเดียวกันพิจารณาพื้นที่สามเหลี่ยม ABC โดยใช้ a เป็นฐานและ EA แทนความสูงจะได้
(a x c sin (180-B)) / 2 = (a x b sin C) /2
(a x c sin B) / 2 = (a x b sin C) /2
ดังนั้น sin B / b = sin C / c
สรุปได้ว่า sin A / a = sin B / b = sin C / c
การใช้กฎของไซน์ กฎของไซน์ประกอบด้วยตัวแปรทั้งสิ้น 4 ตัวแปรคือ มุมและด้านตรงข้ามมุม จำนวนสองคู่นั้นหมายความว่า หากเรารู้ขนาดมุมและด้านตรงความมุมคู่หนึ่ง หากเรารู้ขนาดมุมที่เหลือ เราจะสามารถหาขนาดของด้านที่เหลือได้ เช่นเดียวกันหากเรารู้ขนาดด้านที่เหลือเราจะสามารถหาขนาดของมุมที่รองรับด้านนั้นได้ดัง
ตัวอย่างที่ 1 กำหนดสามเหลี่ยมในภาพที่ 5 จงหามุม B
ภาพที่ 5 ภาพประกอบตัวอย่างที่ 1
โดยวีระ ยุคุณธร
จะเห็นว่าเราทราบค่า มุม C และ ขนาดด้าน c ถ้าเรารู้ขนาดของด้าน b เราจะสามารถหามุม B ได้จาก sin C / c = sin B / b
นั้นคือ B = arcsin { (bsin C)/c } = 60.1 เป็นไปตามภาพที่ 6
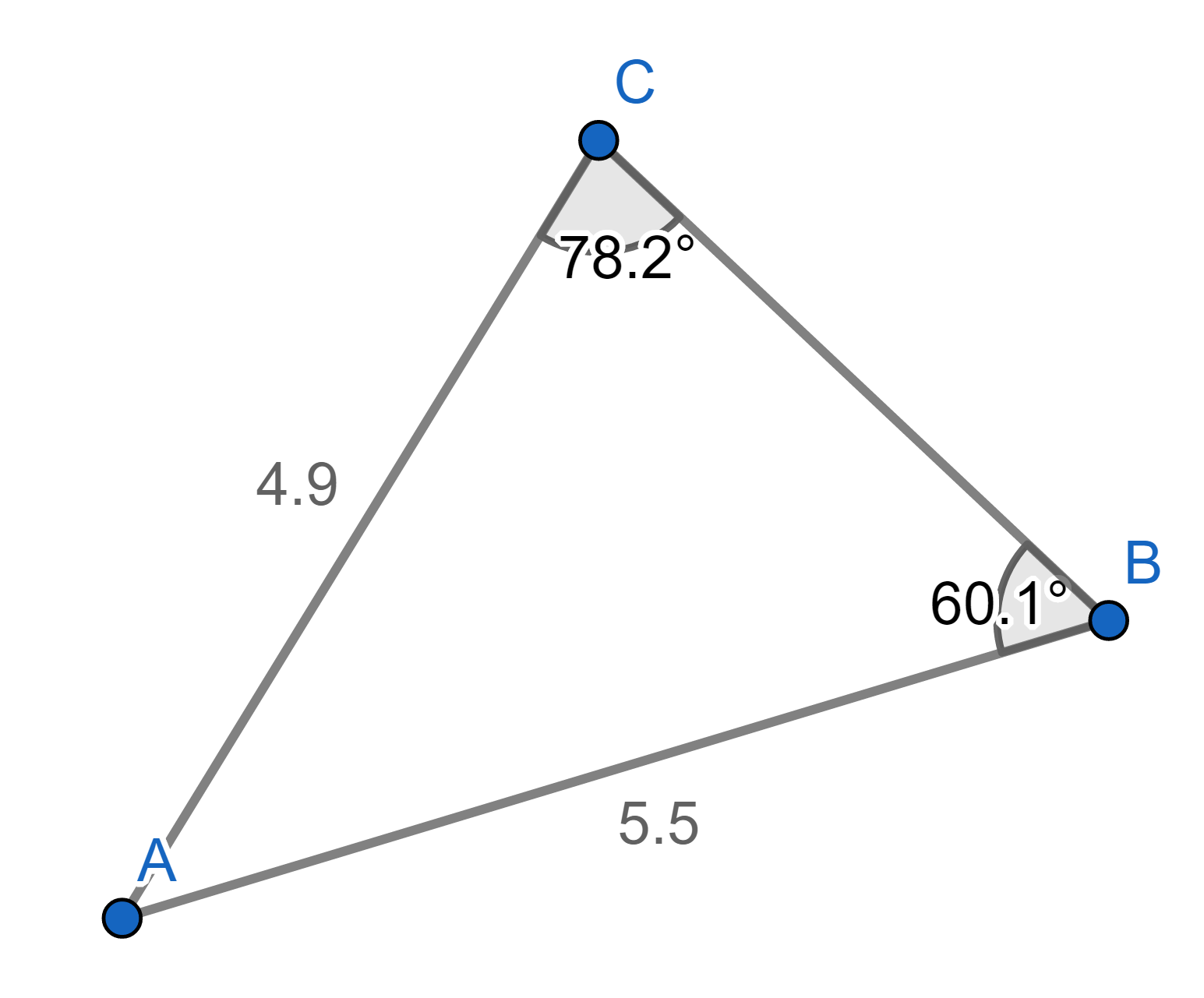
ภาพที่ 6 ภาพเฉลยตัวอย่างที่ 1
โดยวีระ ยุคุณธร
ตัวอย่างที่ 2 กำหนดสามเหลี่ยมในภาพที่ 7 จงหาขนาด b
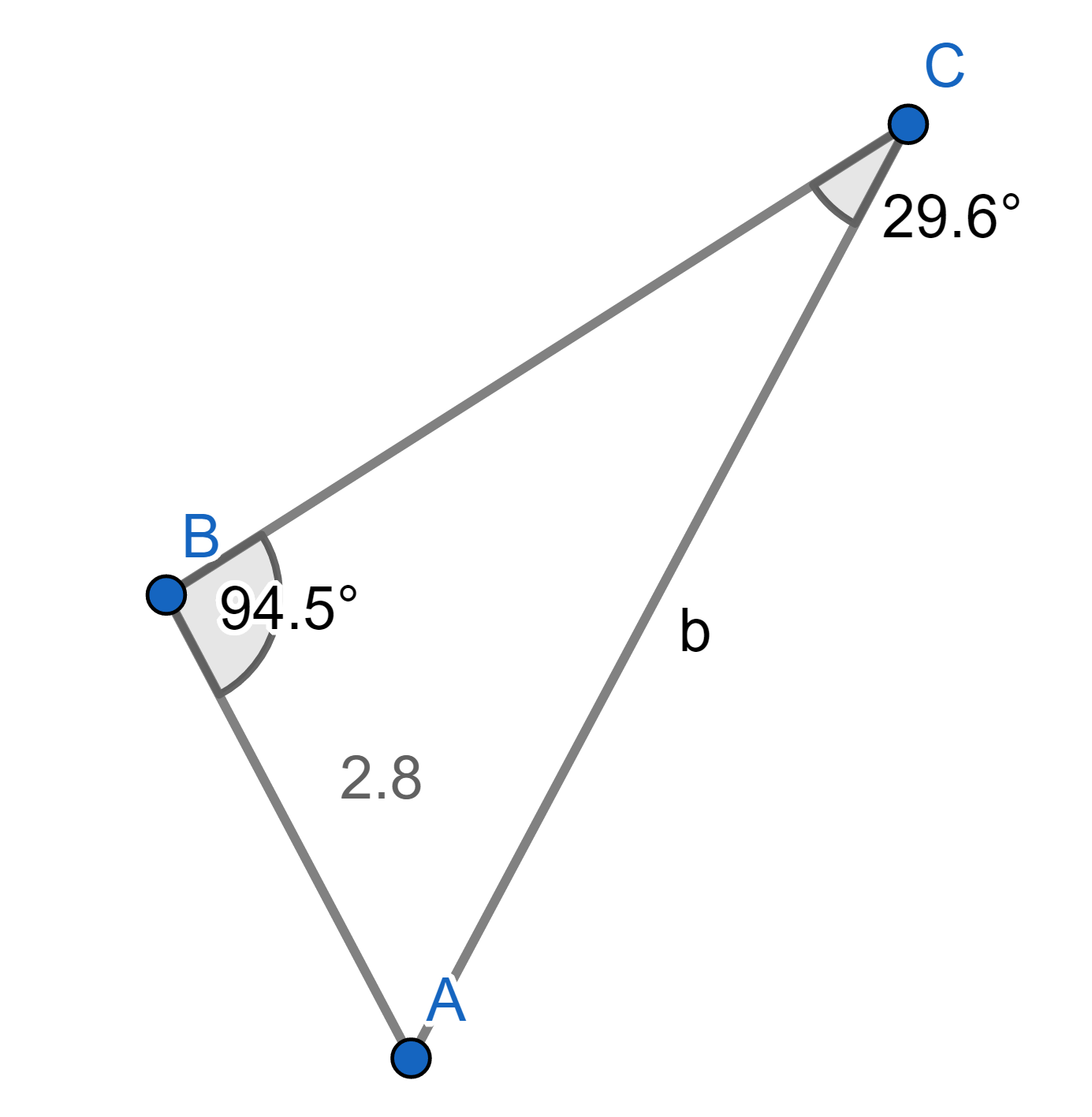
ภาพที่ 7 ภาพประกอบตัวอย่างที่ 2
โดยวีระ ยุคุณธร
จะเห็นว่าเรารู้ความยาวด้าน c และ มุม C ขณะเดียวกันทราบขนาดมุม B เราสามารถหาความยาวด้านตรงข้ามมุม B ได้จาก sin C / c = sin B / b จะได้ว่า b = c (sin B)/ (sin C) = 5.6 ดังเฉลยในภาพที่ 8
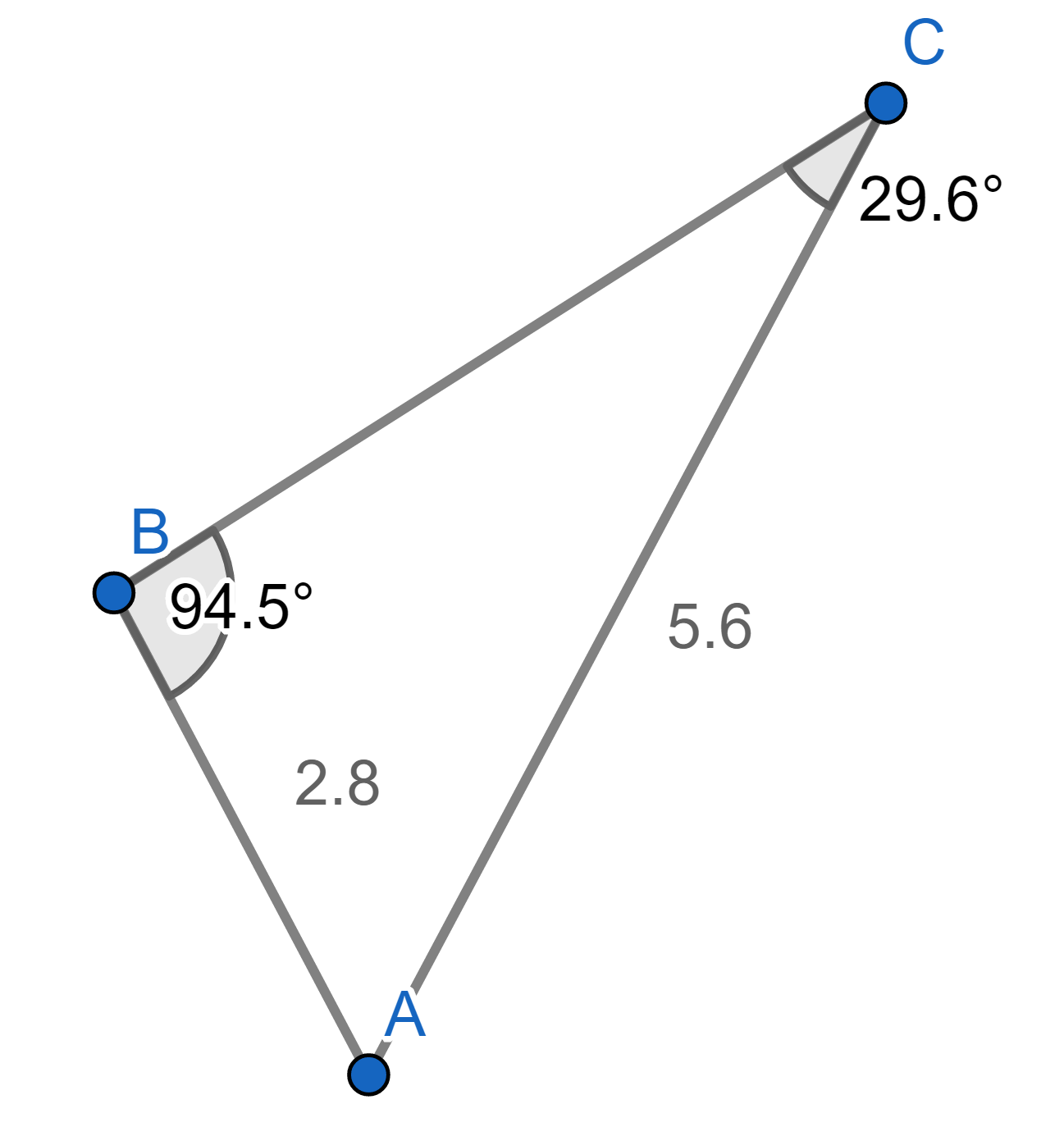
ภาพที่ 8 ภาพเฉลยตัวอย่างที่ 2
โดยวีระ ยุคุณธร
กฏของโคไซน์
กำหนดรูปสามเหลี่ยมใด ๆ มีความยาวด้านตรงข้ามมุม A, B และ C มีขนาด a, b และ c หน่วยตามลำดับดังภาพที่ 5
ภาพที่ 9 รูปสามเหลี่ยมประกอบการพิสูจน์กฎของโคไซน์
โดยวีระ ยุคุณธร
เมื่อพิจารณาความสูง CD จะพบว่า CD = asinB หรือ CD =bsinA
เมื่อใช้ร่วมกับทฤษฎีพิธากอรัสสำหรับสามเหลี่ยม BCD จะได้ b2 = (a sinB)2 + (c – a cosB)2 = a2 + c2 – 2(ac)cos B
แต่ถ้าใช้ร่วมกับทฤษฎีพิธากอรัสสำหรับสามเหลี่ยม ACD จะได้ a2 = (b sinA)2 + (c – b cosA)2 = b2 + c2 – 2(bc)cos A
สามารถพิสูจน์ได้ในทำนองเดียวกันว่า
c2 = a2 + b2 – 2(ab)cos C
เอกลักษณ์สามข้อต่อไปนี้
a2 = b2 + c2 – 2(bc)cos A
b2 = c2 + a2 – 2(ac)cos B
c2 = a2 + b2 – 2(ab)cos C
เรียกว่ากฎของโคไซน์
การใช้กฎของโคไซน์ ตัวแปรในกฎของโคไซน์ประกอบด้วยความยาวด้านสามด้านและ มุม 1 มุม นั้นความหมายว่ากรณีที่ 1 หากเราทราบความยาวด้าน 2 ด้านและมุมระหว่างด้านทั้งสอง เราจะสามารถหาความยาวด้านตรงข้ามมุมนี้ได้ และ กรณีที่ 2 หากเราทราบความยาวด้าน 3 ด้านเราจะสามารถหาขนาดของมุมในรูปสามเหลี่ยมได้
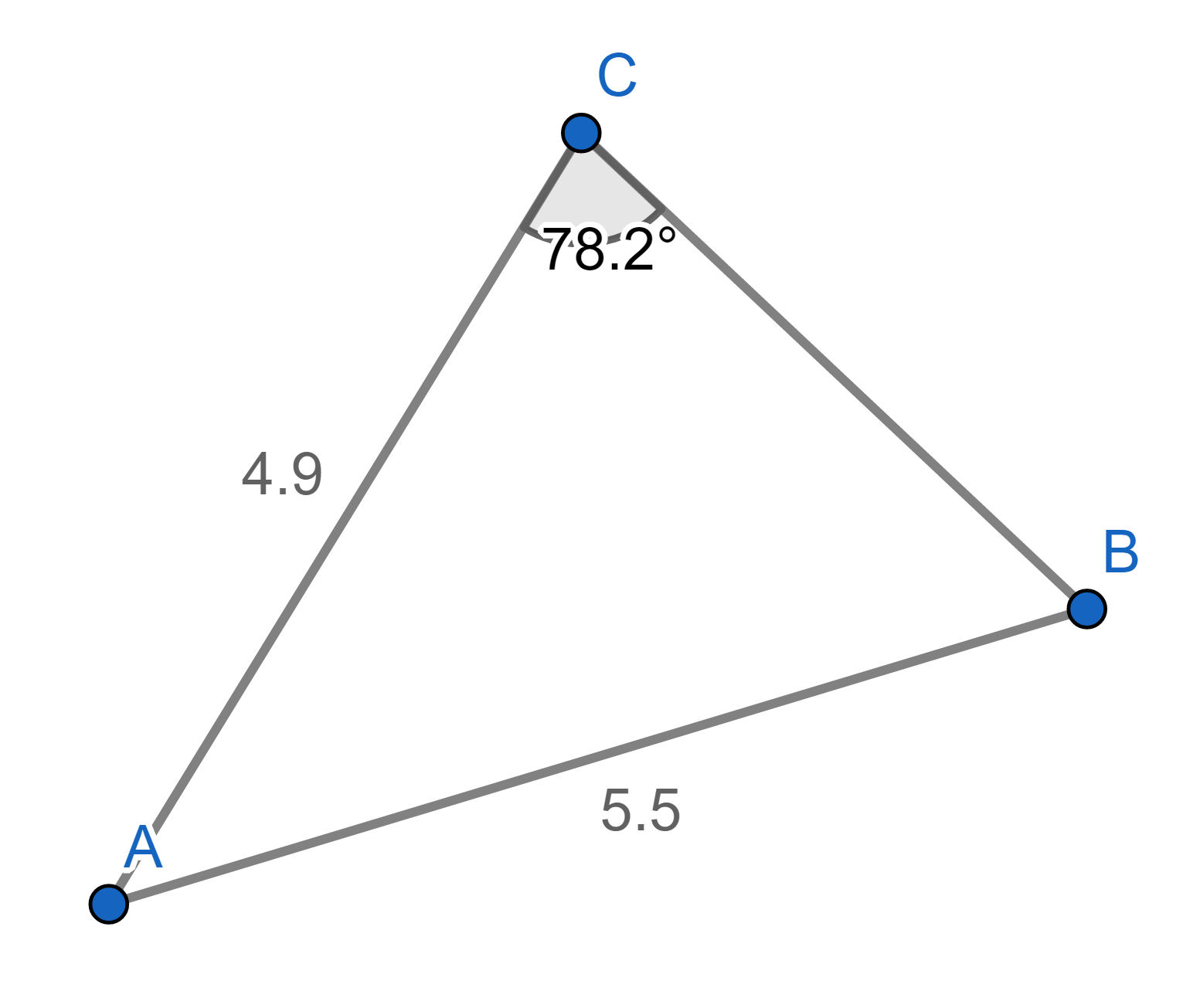
ตัวอย่างที่ 3 จงหาขนาด CB
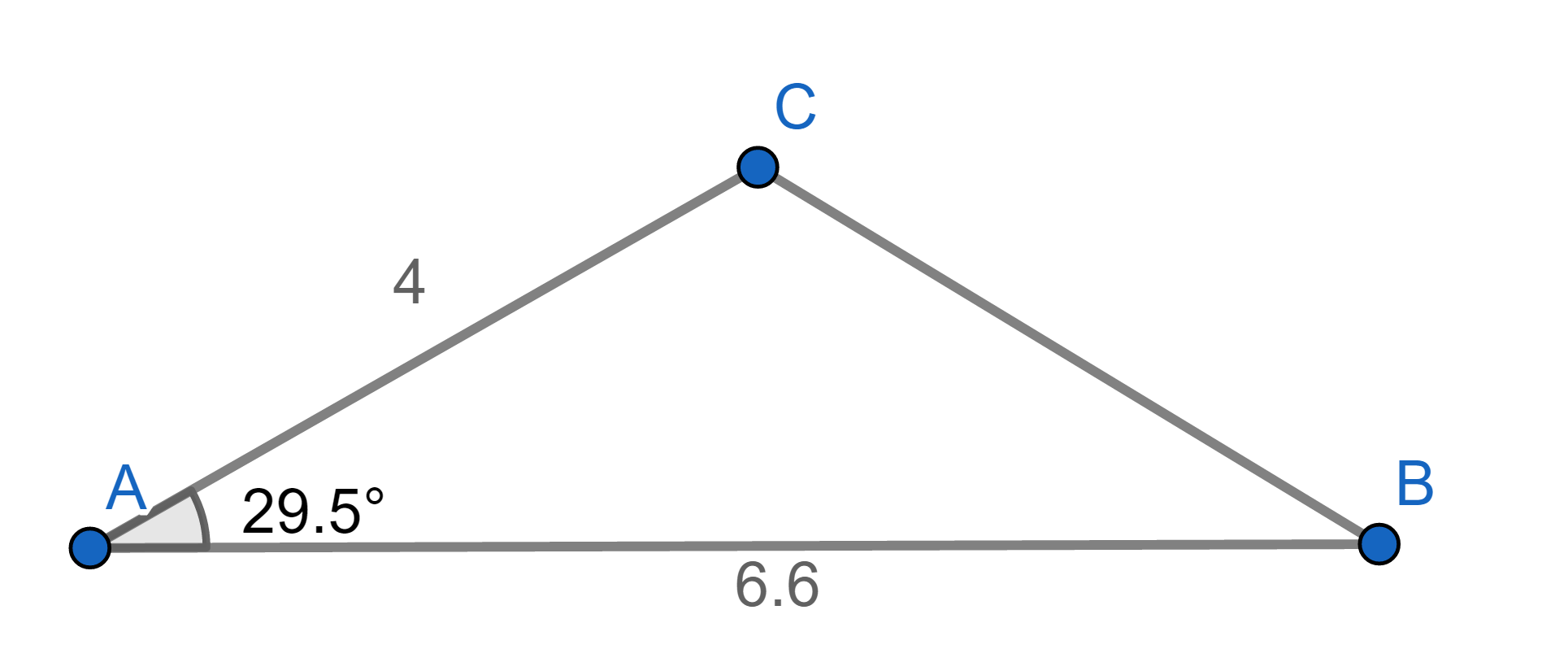
ภาพที่ 10 ภาพประกอบตัวอย่างที่ 3
โดยวีระ ยุคุณธร
CB2 = AC2 + AB2 -2(AC)(AB)cos A = 14 จะได้ CB ประมาณ 3.7 ดังภาพที่ 11
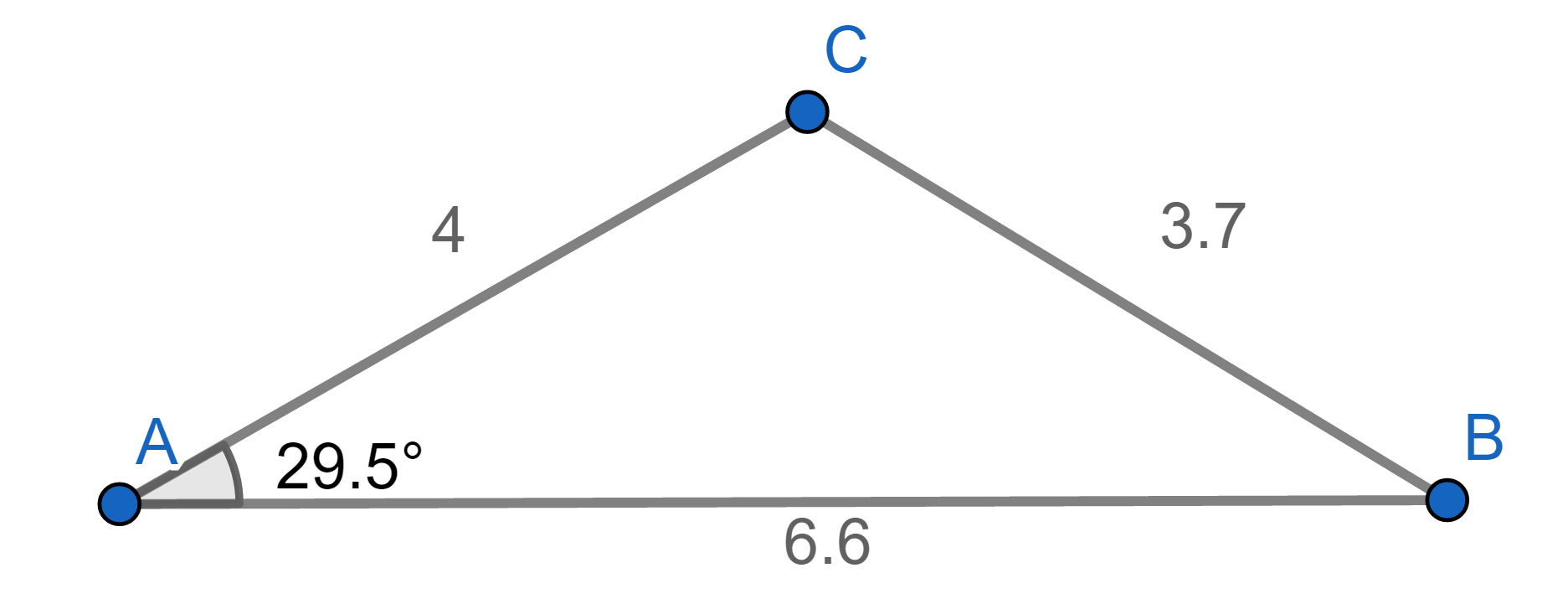
ภาพที่ 11 ภาพเฉลยตัวอย่างที่ 3
โดยวีระ ยุคุณธร
แหล่งที่มา
Patrick D. Barry. Geometry with Trigonometry. Horwood. Chichester. 2001. ISBN 1-898563-69-1.
Junior Cycle Course Committee, NCCA. Mathematics: Junior Certificate Guidelines for Teachers. Stationary Office, Dublin. 2002. ISBN 07557-1193-9.
Fiacre O’Cairbre, John McKeon, and Richard O. Watson. A Resource for Transition Year Mathematics Teachers. DES. Dublin. 2006.83
Anthony G. O’Farrell. School Geometry. IMTA Newsletter 109 (2009) 21-28.
กลับไปที่เนื้อหา



