สำหรับคำถาม “ คณิตศาสตร์คืออะไร ? ” นั้น การพยายามตอบหรือให้คำจำกัดความ ดูจะเป็นเรื่องท้าทายและสุ่มเสี่ยงต่อการวิพากษ์วิจารณ์ ทว่าการพยายามให้ความหมายแม้จะไม่มีทางหาความสมบูรณ์แบบพบก็ตาม ก็ยังดูประหนึ่งว่าเป็นกิจกรรมทางวิชาการที่ท้าทายชวนคิดอยู่ไม่น้อย ยิ่งในโลกหลังยุคสมัยใหม่ ( Post – modern ) ที่มีอิทธิพลของแนวคิดปรัชญาหลังยุคสมัยใหม่อบอวลอยู่อาจจะมีผู้มองว่าความพยายามในการให้นิยามความหมายของอะไรก็ตามดูจะเป็นเรื่อที่มีสาระน้อย และเป็นความพยายามที่จะแช่แข็งความหมาย อีกทั้งจำกัดเนื้อหาสาระของเรื่องนั้น ๆ

กระนั้นก็ตาม ในฐานะที่เป็นกิจกรรมทางปัญญา การพยายามตอบคำถามที่ว่า “ คณิตศาสตร์คืออะไร ? ” ได้ผ่านมาหลายยุคสมัย ก่อนที่แนวคิดหลังยุคสมัยใหม่จะมาถึง ดังเช่นถ้าคำตอบของคณิตศาสตร์คือ การศึกษาในเรื่องจำนวนและตัวเลข คำตอบเช่นนี้คงทันสมัยและเพียงพอแก่การอธิบายในช่วง 2,500 ปีที่แล้ว ที่พอจะพบหลักฐานเกี่ยวกับตัวเลขทางคณิตศาสตร์ของชาวอียิปต์โบราณ ชาวบาบิโลเนียน และชาวจีน

ยิ่งสำหรับชาวกรีกแล้ว พวกเขาเน้นที่เรขาคณิต คณิตศาสตร์ของพวกเขาก็คือ จำนวนและรูปทรง หลังจากยุคกรีก แม้ความรู้ทางคณิตศาสตร์จะก้าวหน้าในหลาย ๆ ส่วนของโลก ดังเช่นที่มีชื่อเสียงในแถบอาระเบียและจีน ลักษณะของคณิตศาสตร์ก็ยังไม่ได้เปลี่ยนแปลงไปมากนัก จนกระทั่งกลางคริสต์ศตวรรษที่ 17 เมื่อนิวตัน ( Newton ) ชาวอังกฤษและไลบ์นิทซ์ ( Leibniz ) ชาวเยอรมันต่างก็พัฒนาแคลคูลัสขึ้นมา ซึ่งโดยสารัตถะของแคลคูลัสแล้ว คือการศึกษาในเรื่องการเปลี่ยนแปลง ( Change ) และการเคลื่อนที่ ( Motion ) ด้วยเทคนิคใหม่นี้ ทำให้นักคณิตศาสตร์สามารถศึกษาการตกสู่พื้นโลกของวัตถุ การทำงานของจักรกล การไหลของของเหลว การขยายตัวของก๊าซ การเติบโตของพืชและสัตว์ รวมไปถึงการกวัดแกว่งของผลกำไร พูดง่าย ๆ คณิตศาสตร์สมัยใหม่ขยายขอบเขตไปสู่การศึกษาในเรื่อง จำนวน รูปทรง การเคลื่อนที่ ความเปลี่ยนแปลงและมิติพื้นที่ ( Space ) ฯลฯ

จวบจนยุคปัจจุบัน การจัดแบ่งประเภทในการศึกษาคณิตศาสตร์อาจจำแนกได้ถึง 60 – 70 หัวข้อวิชาทีเดียว อีกทั้งบางหัวข้อยังแยกย่อยแตกแขนงออกไปอีก ดังเช่นวิชา Algebra หรือ Topology

ท่ามกลางความหลากหลายดังเช่นในทุกวันนี้คำถามว่า “ คณิตศาสตร์คืออะไร ? ” นักคณิตศาสตร์ในปัจจุบัน ถ้าหากจะต้องตอบคำถาม จะให้คำตอบเช่นไร ในหนังสือ THE MATH GENE ของ Keith Devlin ให้คำตอบที่น่าสนใจว่า คณิตศาสตร์คือศาสตร์ที่ว่าด้วย รูปแบบ / แบบแผนต่าง ๆ ( the science of patterns ) แม้จะฟังดูแล้วมีมิติที่กว้างไกลและดูมีลักษณะเป็นการครอบจักรวาลไปบ้าง หรือมีลักษณะเป็น blanket theory อยู่บ้าง

การศึกษาคณิตศาสตร์สำหรับ Devlin ก็คือ การพยายามอธิบายถึงโครงสร้าง ความสัมพันธ์ ระเบียบ รูปแบบ / แบบแผนต่าง ๆ ทั้งที่อยู่ในธรรมชาติรอบตัวและที่อยู่ในมโนทัศน์ เท่าที่มนุษย์จะสามารถรับรู้ได้ทั้งในเชิงนามธรรมและรูปธรรม โดยอาศัยภาษาทางคณิตศาสตร์มาอธิบาย



รูปแบบ / แบบแผนที่หลากหลายแตกต่างกันนำไปสู่ความหลากหลายในแขนงสาขาวิชาคณิตศาสตร์ ตัวอย่างเช่น ทฤษฎีจำนวนศึกษารูปแบบ / แบบแผนของจำนวนและการนับ เรขาคณิตศึกษาถึงรูปแบบ / แบบแผนของรูปทรง แคลคูลัสทำให้เราสามารถอธิบายรูปแบบ / แบบแผนของการเคลื่อนที่ ตรรกศาสตร์ศึกษาถึงรูปแบบ / แบบแผนของการให้เหตุผล ทฤษฎีความน่าจะเป็นเกี่ยวข้องกับรูปแบบ / แบบแผนของโอกาส ทอพอโลยี ( Topology ) นั้นศึกษารูปแบบ / แบบแผนของการปิดล้อมและการวางตำแหน่ง ( closeness and position )

ด้วยการศึกษาความสัมพันธ์ รูปแบบ / แบบแผนต่าง ๆ โดยนักคณิตศาสตร์ สามารถนำไปศึกษาสิ่งใด ๆ ก็ได้ในธรรมชาติ เช่น รูปแบบ / แบบแผนที่สมมาตรกันของดอกไม้ แบบแผนที่ซับซ้อนของเงื่อนปมต่าง ๆ ( knots ) วงโคจรของกระสวยอวกาศที่โคจรนอกโลก แบบแผนของลายจุดบนแผ่นหนังของเสือดาว รูปแบบ / แบบแผนการลงคะแนนเสียงของประชาชนในเขตเลือกตั้ง แบบแผนของผลลัพธ์เชิงสุ่มในการทอยลุกเต๋าหรือรูเล็ต แบบแผนของเสียงที่มนุษย์เห็นว่าเป็นเสียงดนตรี

Devlin เห็นว่าถ้าโลกนี้ปราศจากนักคณิตศาสตร์ เราคงไม่เข้าใจว่าอะไรทำให้ชิ้นเหล็กขนาดใหญ่อย่างเครื่องบินจัมโบ้เจ็ทลอยอยู่ได้ในอากาศโดยที่ไม่มีอะไรยกมันไว้ ถ้าไม่ใช่นักคณิตศาสตร์ที่ชื่อ Daniel Bernoulli ในต้นศริสต์ศตวรรษที่ 18 ที่พบสมการทางแคลคูลัสซึ่งทำให้เรา “ เห็น ” ถึงสิ่งที่ทำให้เครื่องบินยกตัวขึ้นได้

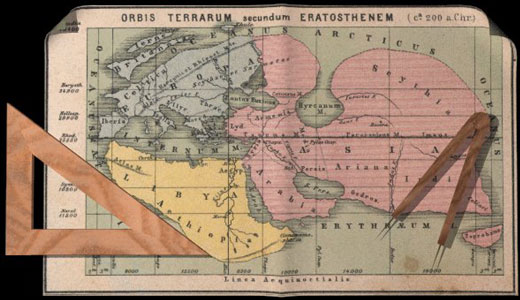
หรือเมื่อกว่าสองพันปี ก่อนที่เราจะสามารถสร้างยานอวกาศออกไปนอกโลกเพื่อถ่ายภาพโลกขอเรา นักคณิตศาสตร์ชาวกรีกชื่อ Eratosthenes ใช้คณิตศาสตร์เพื่อแสดงให้เห็นว่าโลกนั้นมีสัณฐานกลม หรือกล่าวอีนัยหนึ่งได้ว่าภาษาทางคณิตศาสตร์ทำให้สิ่งที่มองไม่เห็นมองเห็นได้ นี่เองเป็นที่มาของหนังสือเล่มหนึ่งที่ Devlin เขียนขึ้นในปี ค.ศ. 1998 โดยใช้ชื่อว่า “ The Language of Mathematics : Making the Invisible Visible ”

อีกตัวอย่างหนึ่งที่น่าสนใจคือ ในทศวรรษที่ 1950 Noam Chomsky นักคณิตศาสตร์ นักภาษาศาสตร์และเป็นอีกหลาย ๆ นัก ซึ่งในปัจจุบันมีบทบาทอย่างสูงในการวิพากษ์วิจารณ์สังคมการเมืองของโลก ได้ใช้คณิตศาสตร์เพื่อให้ “ มองเห็น ” สิ่งที่มองไม่เห็น นั่นคือ รูปแบบ / แบบแผนเชิงนามธรรมของคำต่าง ๆ ที่ประกอบกัน ซึ่งเรายอมรับว่าเป็นประโยคที่ถูกต้องตามหลักไวยากรณ์ ดังนั้นเขาจึงเป็นผู้เปลี่ยนวิชาภาษาศาสตร์จากสาขาที่คลุมเครือมาสู่ความรุ่งเรืองแบบวิทยาศาสตร์

เมื่อคณิตศาสตร์คือการศึกษาเพื่อทำความเข้าใจถึงรูปแบบ / แบบแผนซึ่งทำให้เรามอง “ เห็น ” ในสิ่งที่มองไม่เห็น บางครั้งทำให้เราสามารถมอง “ เห็น ” ถึงอนาคตกาลได้ด้วย แม้ว่าอาจจะมีความคลาดเคลื่อนอยู่บ้าง ดังเช่น ทฤษฎีความน่าจะเป็นและสถิติศาสตร์ ทำให้เราสามารถพยากรณ์ผลลัพธ์ของการเลือกตั้ง เราสามารารถใช้แคลคูลัสพยาการณ์อากาศในวันพรุ่งนี้ นักวิเคราะห์ตลาดหุ้น ใช้ทฤษฎีทางคณิตศาสตร์อธิบายพฤติกรรมของตลาดหุ้น บริษัทประกันภัยใช้สถิติและความน่าจะเป็นเพื่อคำนวณแนวโน้มของการเกิดอุบัติเหตุในปีที่จะมาถึง เพื่อกำหนดเบี้ยประกันภัยให้สอดคล้อง

ที่กล่าวมาทั้งหมดนี้ เป็นความพยายามที่จะให้ความหมายของคณิตศาสตร์ ซึ่งแน่นอนว่าการให้นิยามความหมายเช่นนี้เราคงต้องตระหนักว่า “ ความหมายของคณิตศาสตร์คืออะไร ” หาได้มีความคงตัวดังเช่นค่าคงตัวบางจำพวกในวิชาคณิตศาสตร์ไม่ เพราะว่าพัฒนาการของคณิตศาสตร์มิได้หยุดนิ่งอยู่กับที่ ความหมายของคณิตศาสตร์ที่ว่า คือ ศาสตร์ว่าด้วยรูปแบบ / แบบแผนต่าง ๆ จึงรอการตรวจสอบและการพิสูจน์ผิด ( falsification ) อยู่ทุกเมื่อเชื่อวัน