1. การบวกและลบเวกเตอร์

สมมติเรามีเวกเตอร์และที่มีขนาดและทิศทางดังรูป

จะเรียกปลายที่มีลูกศรว่า “หัว” และเรียกอีกปลายที่ไม่มีลูกศรว่า “หาง”

ถ้าต้องการรวม 2 เวกเตอร์นี้เข้าด้วยกัน นั่นคือหาผลลัพธ์ของ+เราสามารถทำได้ 2 วิธี ดังนี้

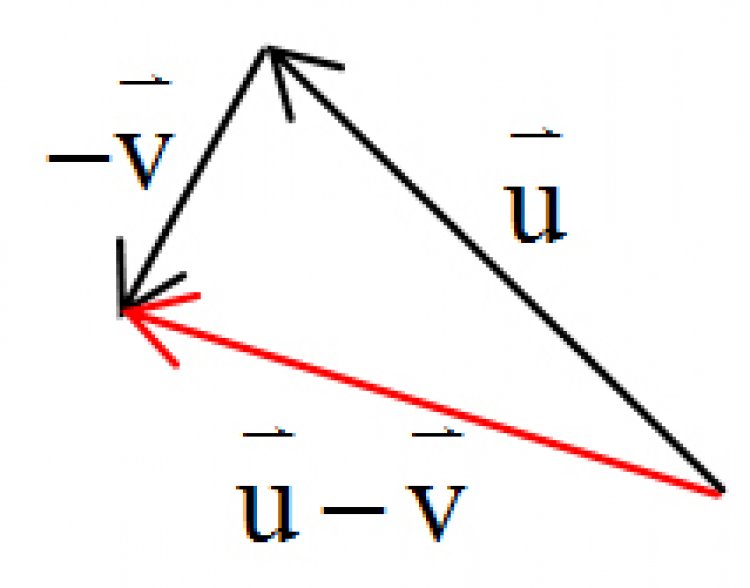
1. แบบหัวต่อหาง: เขียนเวกเตอร์ก่อน จากนั้นเอาหางของมาต่อที่หัวของดังรูป
ผลลัพธ์ที่ได้คือเวกเตอร์ที่ลากจากหางของไปสิ้นสุดที่หัวของ

2. แบบหางต่อหาง: นำหางของทั้งสองเวกเตอร์มาต่อชนกันแล้วสร้างรูปสี่เหลี่ยมด้านขนาน(แสดงด้วยเส้นประสีเทา)ผลลัพธ์ที่ได้คือเวกเตอร์ที่ลากจากจุดหางที่ต่อกัน ไปจนถึงมุมทะแยงตรงข้ามของรูปสี่เหลี่ยมด้านขนานนั้น

จะเห็นได้ว่า เวกเตอร์ผลลัพธ์ที่ได้จากทั้งสองวิธีนี้เท่ากัน โดยมีขนาดและทิศทางดังแสดงตามลูกศรสีแดง

สำหรับการลบกันของเวกเตอร์ จริงๆ แล้วก็คือการบวกด้วยเวกเตอร์ที่เป็นลบ เช่น-=+(-) จากนั้นก็ดำเนินการต่อด้วยวิธีการที่กล่าวไปแล้วข้างต้น

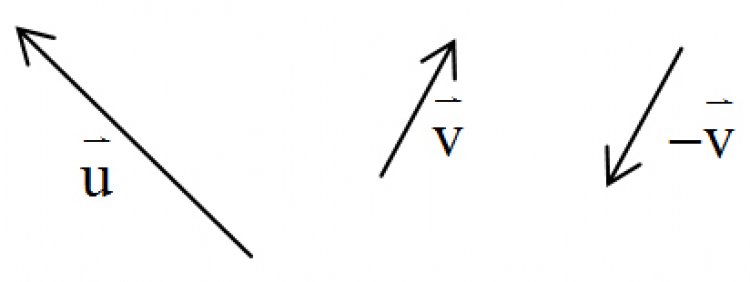
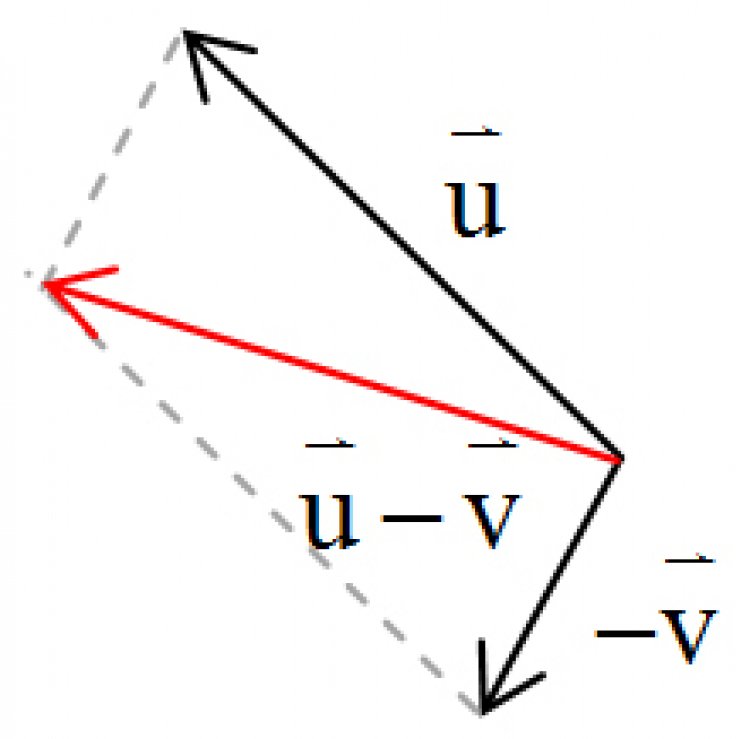
แปลงเวกเตอร์เป็น - ใช้วิธีหัวต่อหาง ใช้วิธีหางต่อหาง

2. เวกเตอร์ในระบบพิกัดฉาก 2 มิติ และ 3 มิติ

ลองดูรูปต่อไปนี้

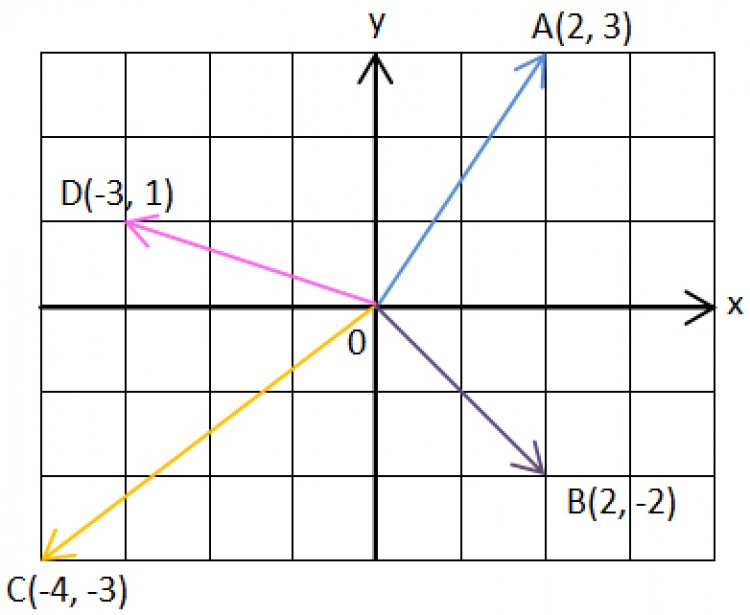
จากรูป,,และเป็นเวกเตอร์ใน 2 มิติ ซึ่งต่างก็มีจุดเริ่มต้นที่จุดกำเนิด (0, 0)

คือ ผลบวกของเวกเตอร์ 2 หน่วยในแกน +x กับเวกเตอร์ 3 หน่วยในแกน +y ซึ่งจะเขียนได้ว่า

ลองคิดเล่นๆ ว่าเราจะเขียนเวกเตอร์ที่เหลือในเทอมของ i, j ได้อย่างไร?

แล้วเวกเตอร์ 2 มิติที่ไม่ได้เริ่มจากจุดกำเนิดล่ะ เราจะเขียนสมการแทนมันได้อย่างไร?

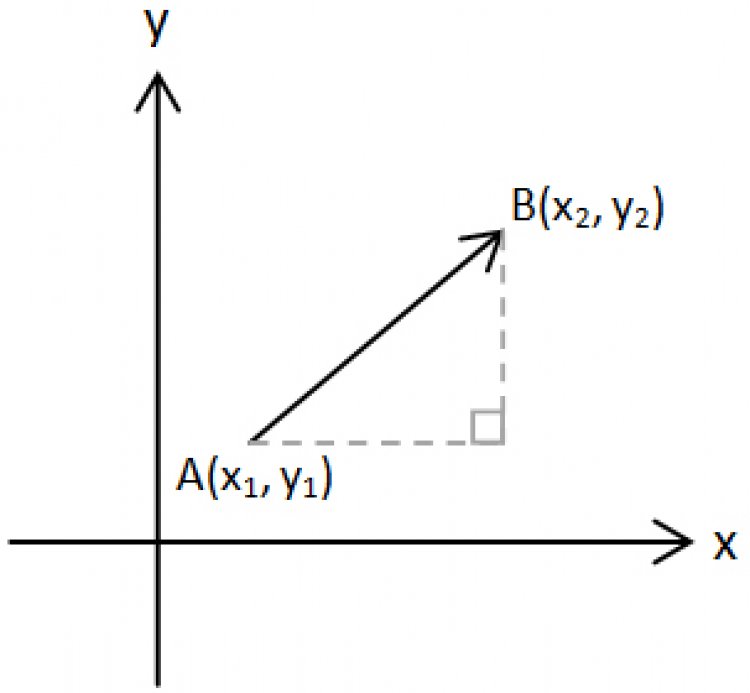
เมื่อเราทราบจุดเริ่ม (A) และจุดปลาย (B) ก็ไม่ยากที่จะเขียนแสดงเวกเตอร์นี้แบบ i, j

ขนาดของหาได้จาก

และจะหาความชัน m ได้ง่ายๆ จาก

เมื่อเริ่มคุ้นเคยกับเวกเตอร์ใน 2 มิติแล้ว ทีนี้เราลองมาดูแบบ 3 มิติทะลุจอกันบ้าง

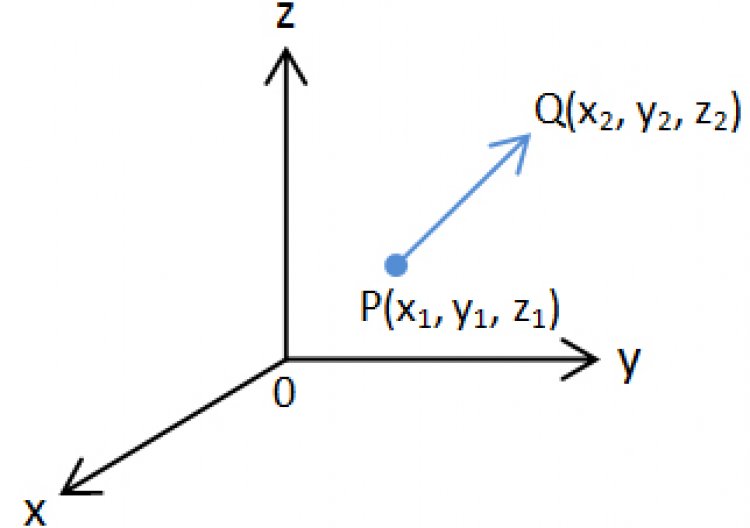
เป็นเวกเตอร์ที่มีจุดเริ่ม (P) และจุดปลาย (Q) ใดๆ ในพิกัด xyz เราจะได้ว่า

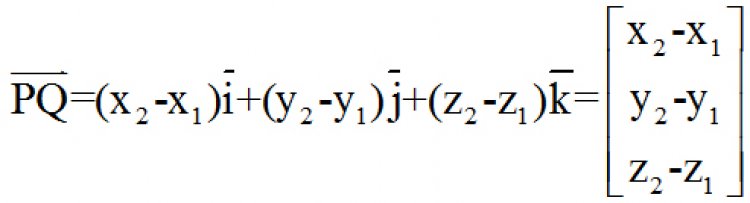
และ

ได้รู้จักเวกเตอร์กันมากขึ้นอีกหน่อยแล้ว งั้นเราลองฝึกทำโจทย์ที่หัวข้อถัดไปกันดีกว่า จะได้รู้ว่าเราเข้าใจเรื่องเวกเตอร์มากน้อยแค่ไหนนะคะ ^_^

3. สารพันการคูณเวกเตอร์

หลังจากได้ลองบวกและลบเวกเตอร์ในหัวข้อก่อนๆ แล้ว ในหัวข้อนี้เราจะลองคูณเวกเตอร์กัน

แต่ขึ้นชื่อว่าเป็นปริมาณเวกเตอร์ จะให้คูณแบบเบสิคๆเหมือนตัวเลขทั่วไปคงไม่ได้ มาดูกันดีกว่าว่าจะทำอย่างไร

การคูณกับเวกเตอร์ อาจแบ่งออกได้เป็น

1. จำนวนสเกลาร์คูณกับเวกเตอร์ เอาตัวเลขปกติคูณกับเวกเตอร์ ได้ผลลัพธ์ออกมาเป็นเวกเตอร์

2. เวกเตอร์คูณแบบดอทกับเวกเตอร์ ได้ผลลัพธ์เป็นสเกลาร์หรือตัวเลขธรรมดาหนึ่งค่า

3. เวกเตอร์คูณแบบครอสกับเวกเตอร์ ได้ผลลัพธ์เป็นเวกเตอร์ โดยทิศของผลลัพธ์จะตั้งฉากกับสองเวกเตอร์ที่คูณกัน

เอาล่ะ มาดูในรายละเอียดกันค่ะ

แบบที่ 1: จำนวนสเกลาร์คูณกับเวกเตอร์

ใน 2 มิติ

เช่น

x

ใน 3 มิติ

เช่น

เมื่อเป็นจำนวนจริงใดๆ

แบบที่ 2:เวกเตอร์คูณแบบดอทกับเวกเตอร์ (Dot product)

การคูณแบบนี้จะให้ค่าเป็นสเกลาร์ (ตัวเลขปกติไม่ใช่เวกเตอร์) ถ้าต้องการหาผลคูณแบบดอทของ

และสามารถหาได้ 2 วิธี ดังนี้

วิธีที่ 1เมื่อคือมุมที่หางของทั้งสองเวกเตอร์ชนกัน และ

เมื่อจะมีค่าบวกลบขึ้นอยู่กับค่า x เพราะฉะนั้นเราจึงสามารถสรุปได้ว่า

- ถ้าจะได้เป็นค่าบวก ดังนั้นได้ผลลัพธ์เป็นบวก

- ถ้าหรือสองเวกเตอร์ตั้งฉากกัน จะได้ดังนั้นผลลัพธ์

- ถ้าจะได้เป็นค่าลบ ดังนั้นผลลัพธ์จึงเป็นลบ

วิธีที่ 2

สำหรับเวกเตอร์ใน 2 มิติ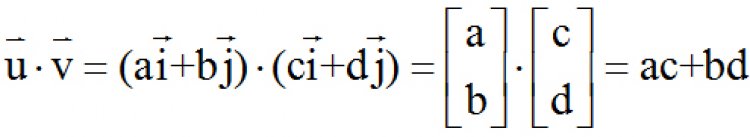

สำหรับเวกเตอร์ใน 3 มิติ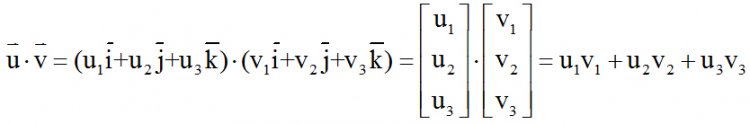

แบบที่ 3:เวกเตอร์คูณแบบครอสกับเวกเตอร์(Cross product)

การคูณแบบนี้จะให้ผลลัพธ์เป็นเวกเตอร์

ถ้า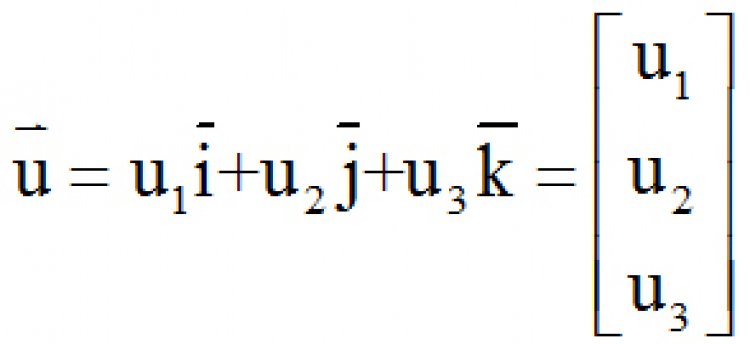และจะได้ว่า

โดยมีทิศของผลลัพธ์เป็นไปตามกฎมือขวา ดังนี้

1) แบมือขวา ให้นิ้วทั้งสี่ (ชี้-ก้อย) ชี้ไปตามทิศของเวกเตอร์ตัวตั้ง () แล้วพับนิ้วเข้าหาทิศของตัวคูณ ()

นิ้วหัวแม่มือจะชี้ในทิศผลลัพธ์ของ

2) ถ้านิ้วทั้งสี่ชี้ไปตามทิศแล้วพับนิ้วเข้าหาทิศของนิ้วหัวแม่มือจะชี้ในทิศ

ขนาดของหาได้จากเมื่อคือมุมที่หางของทั้งสองเวกเตอร์ชนกัน และ

4. การหาพื้นที่สี่เหลี่ยมด้านขนานจากขนาดของผลคูณเชิงเวกเตอร์ (Cross product)

ทราบมั้ยคะว่า เราสามารถประยุกต์ใช้ความรู้เรื่องผลคูณเชิงเวกเตอร์ ไปใช้ในการหาพื้นที่ของสี่เหลี่ยมด้านขนานได้ด้วยล่ะ

จากรูปข้างต้น จะได้ว่า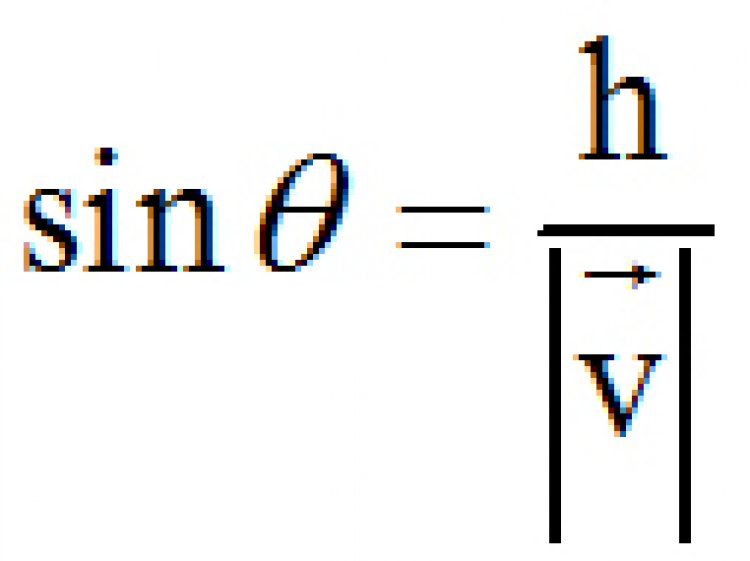

ดังนั้น

เนื่องจาก

เพราะฉะนั้น = พื้นที่ของสี่เหลี่ยมด้านขนาน